Файл: Работы лабораторного практикума.docx

Прибор состоит из сосуда с делениями, наполненного водой; водяного манометра и капилляра. Когда из сосуда выливается вода, при открытом кране, давление внутри сосуда понижается и через капилляр засасывается воздух через осушитель. Благодаря внутреннему трению, давление на концах капилляра становится неодинаковым: Р₁ и Р₂. Разность этих давлений измеряется водяным манометром.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА ИЗМЕРЕНИЙ

1. Ознакомиться с теорией вопроса по описанию и предлагаемой литературе.

2. Проградуировать сосуд с нанесенными на нем метками. Для этого заполнить его водой и с помощью мензурки определить объем воды, которая выливается при опускании уровня воды в сосуде от одной (а) до другой (b) метки. Снова заполнить сосуд с водой выше метки а.

3. Открыть кран и выждать, пока не установится стационарное течение. Признаком этого будет постоянство значения с течением времени.

4. Как только уровень воды установится против метки, включить секундомер и определить время, за которое известный объем воздуха (между делениями а и b) вытечет из сосуда.

5. Измерить температуру воздуха и атмосферное давление в лаборатории.

6. Для определения в системе СГС, учесть, что 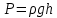, где 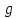=981 см/ , 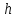– разность уровней жидкости в манометре.

7. Вычислить значения μ и λ

8. Опыт провести пять раз при неизменном значении h, занося результаты в таблицу.

9. Оценить, применим ли рассматриваемый метод для определения вязкости воздуха на предложенной установке. Выводы с расчетами занести в отчет.

ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ.

1. 
   Что понимается под явлением переноса? Приведите примеры.
   
2. 
   В чем заключается явление вязкости газов и жидкостей.
   
3. 
   Поясните, в чем заключается метод измерения вязкости на данной установке. Можно ли таким образом измерить вязкость жидкости?
   
4. 
   Запишите формулы Ньютона для вязкого трения и Пуазейля-Хагена. Поясните смысл величин, входящих в формулы.
   
5. 
   Что понимается под средним значением длины свободного пробега молекулы. Как оно зависит от давления, температуры и концентрации молекул?
   
6. 
   Какова размерность и единицы измерения вязкости в системах СГС и СИ. Выведите соотношения между ними.
   
7. 
   Опишите назначение приборов и принадлежностей в экспериментальной установке и поясните последовательность измерений и расчетов.
   

---

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Поясните механизм возникновения сил внутреннего трения.
   
2. 
   Выведите формулу для силы внутреннего трения, используя молекулярно-кинетическую теорию вещества.
   
3. 
   Выведите формулу Пуазейля-Хагена, и укажите границы ее применимости.
   
4. 
   Проанализируйте, как коэффициент вязкости зависит от давления в газах и жидкостях.
   
5. 
   Проанализируйте, как коэффициент вязкости зависит от температуры в газах и жидкостях. Различия поясните.
   
6. 
   Какими данными вы можете подтвердить справедливость использования формулы Пуазейля для данной лабораторной установки?
   

ТАБЛИЦЫ

Таблица № 5.1

№	Δh см	τ с	V См3	ΔР	η Пз	εη	Δη Пз	λ см	ελ	Δλ см

ЛИТЕРАТУРА
1. Савельев И.В.Курс общей физики. 1987. изучить параграфы:128. Явления переноса, 129. Средняя длина свободного пробега. 132. Вязкость газов.

2. Яковлев В.Ф. Курс физики. Теплота и молекулярная физика. 1976г. 41. Внутреннее трение, 43. Средняя длина свободного пробега. 47. Внутреннее трение в идеальных газах.

3. Сивухин Д.В. Общий курс физики, т. 2, 1975 г. Внутреннее трение и теплопроводность газов.

---

6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ДЛЯ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА.

ЦЕЛИ РАБОТЫ:

1. 
   Изучение метода использования 1 начала термодинамики к исследованию различных термодинамических процессов в идеальных газах.
   
2. 
   Экспериментальное определение отношения молярных теплоёмкостей для воздуха.
   
3. 
   Освоение метода теоретического расчёта теплоёмкостей газов при различных процессах.
   

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:

1. 
   Стеклянный сосуд с двумя кранами.
   
2. 
   U-образный водяной манометр.
   
3. 
   Ручной насос.
   

5. 
   Секундомер.
   

КРАТКАЯ ТЕОРИЯ
Термодинамика изучает системы, состоящие из огромного числа частиц, находящихся в непрерывном хаотическом движении. Методы описания поведения таких сложных систем принципиально отличаются от принятых в механике.

При термодинамическом подходе к изучению таких систем не рассматривают поведение каждой частицы в отдельности и те внутренние механизмы, которые приводят к протеканию тех или иных процессов в системе. Термодинамика использует понятия и физические величины, относящиеся ко всей системе в целом, такие как внутренняя энергия, давление, объём, температура и т. д.

Все теоретические построения термодинамики исходят из весьма общих эмпирических законов, которые называются началами термодинамики.

Первое начало представляет собой закон сохранения и превращения энергии в применении к термодинамическим системам. Количественно I начало формируются следующим образом:

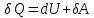. (6.1)

Эта формула означает, что элементарное количество теплоты 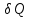, полученное системой, идёт на изменение её внутренней энергии и совершение системой элементарной работы .

С точки зрения статистической физики, внутренняя энергия системы состоит из кинетической энергии поступательного и вращательного движения молекул, колебательного движения атомов, потенциальной энергии взаимодействия молекул и атомов в молекулах. Для идеального газа, где взаимодействие частиц считается пренебрежительно малым, потенциальная энергия взаимодействия принимается равной нулю и формула для расчета внутренней энергии выглядит следующим образом:

---

. (6.2)

Здесь – число степеней свободы молекулы, – масса идеального газа, – молярная масса газа.

Таким образом, внутренняя энергия идеального газа зависит только от температуры и, следовательно, может быть однозначно выражена через макроскопические параметры состояния системы: , , 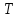. Поэтому говорят, что 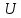есть функция состояния системы. Изменение внутренней энергии в ходе элементарного процесса найдем дифференцированием последнего выражения:

. (6.3)

Изменение внутренней энергии в ходе конечного процесса 1-2 (рис.1) можно найти интегрированием этого уравнения:

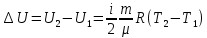. (6.4)

Мы получили, что не зависит от пути перехода системы из состояния 1 в состояние 2, т.к. однозначно определяется через параметры , , 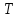конечного и начального состояний.

Рассмотрим элементарную работу 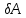. Известная формула из механики для работы может быть преобразована к следующему виду:

. (6.5)

В ходе конечного процесса 1-2 совершается работа

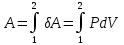. (6.6)

Исходя из геометрического смысла интеграла как площади под кривой, легко видеть, что работа зависит от типа процесса при переходе из 1-2 (т. е. от пути перехода на Рис. 13). Поэтому говорят, что работа является функцией процесса. Для того, чтобы рассчитать интеграл, надо знать, по какому закону изменяются параметры

---

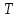, , при переходе 1 2.



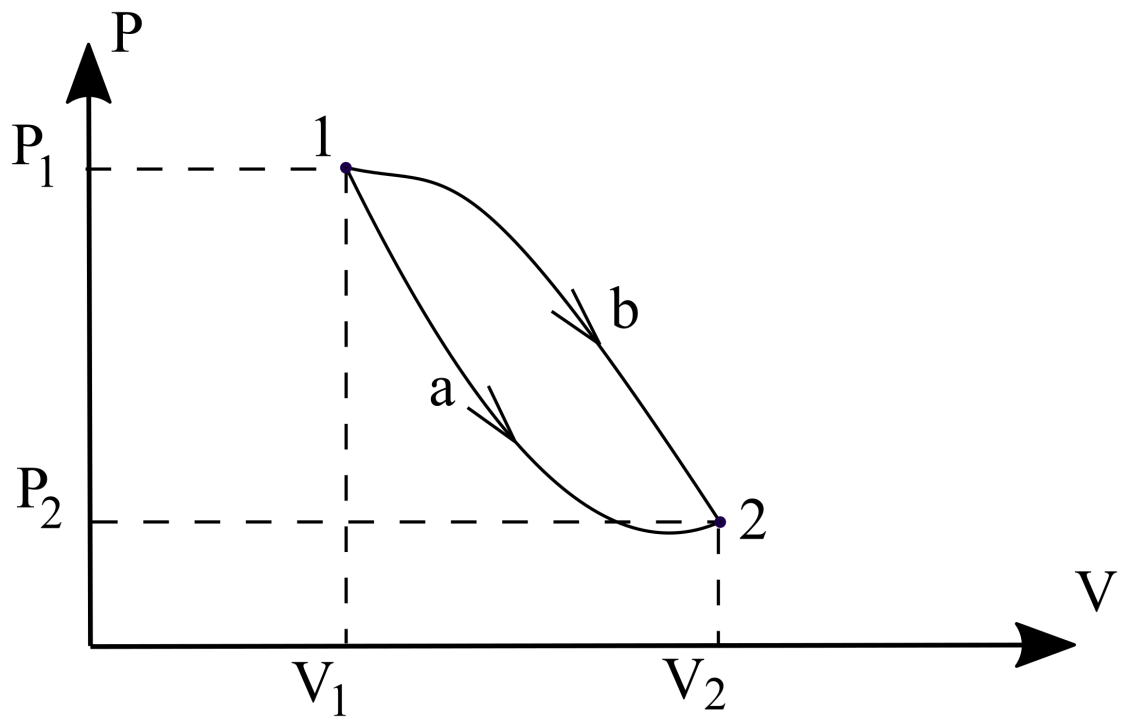
Рисунок 13. Два разных процесса (a и b) с общей начальной и общей конечной точками.

Элементарное количество теплоты, как и работа, является мерой изменения энергии системы в ходе процесса. Как и в случае работы, полное количество теплоты, которое потребуется на совершение процесса 1 2 зависит от того, по какому пути будет развиваться процесс (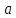 или 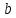на Pис.13), так что теплота Q также является функцией процесса. Принято считать , если тепло поступает в систему и 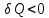, если тепло выходит из системы.

Под теплоемкостью всей системы понимают отношение

, (6.7)

т.е. теплоемкость численно равна количеству тепла, необходимого для изменения температуры на один градус. На практике более часто используются понятия удельной теплоемкости

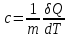, (6.8)

а также молярной теплоемкости

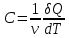, (6.9)

где - количество вещества, выраженное в молях. Поскольку - функция процесса, то и теплоемкости являются функциями процесса, т.е. зависят от того, при каких условиях осуществляется процесс.

Если при нагревании системы её объем остается постоянным, теплоемкость системы называется изохорной и соответствующая молярная теплоемкость обозначается как . Она равна

. (6.10)

Подставив сюда выражение для

---