Файл: Диссертация на соискание ученой степени кандидата технических наук Владимирский государственный университет.doc
Добавлен: 11.01.2024
Просмотров: 346
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Предотвращенный ущерб от 1-й угрозы до и после применения рекомендаций по защите показан на Рисунке 4.2.
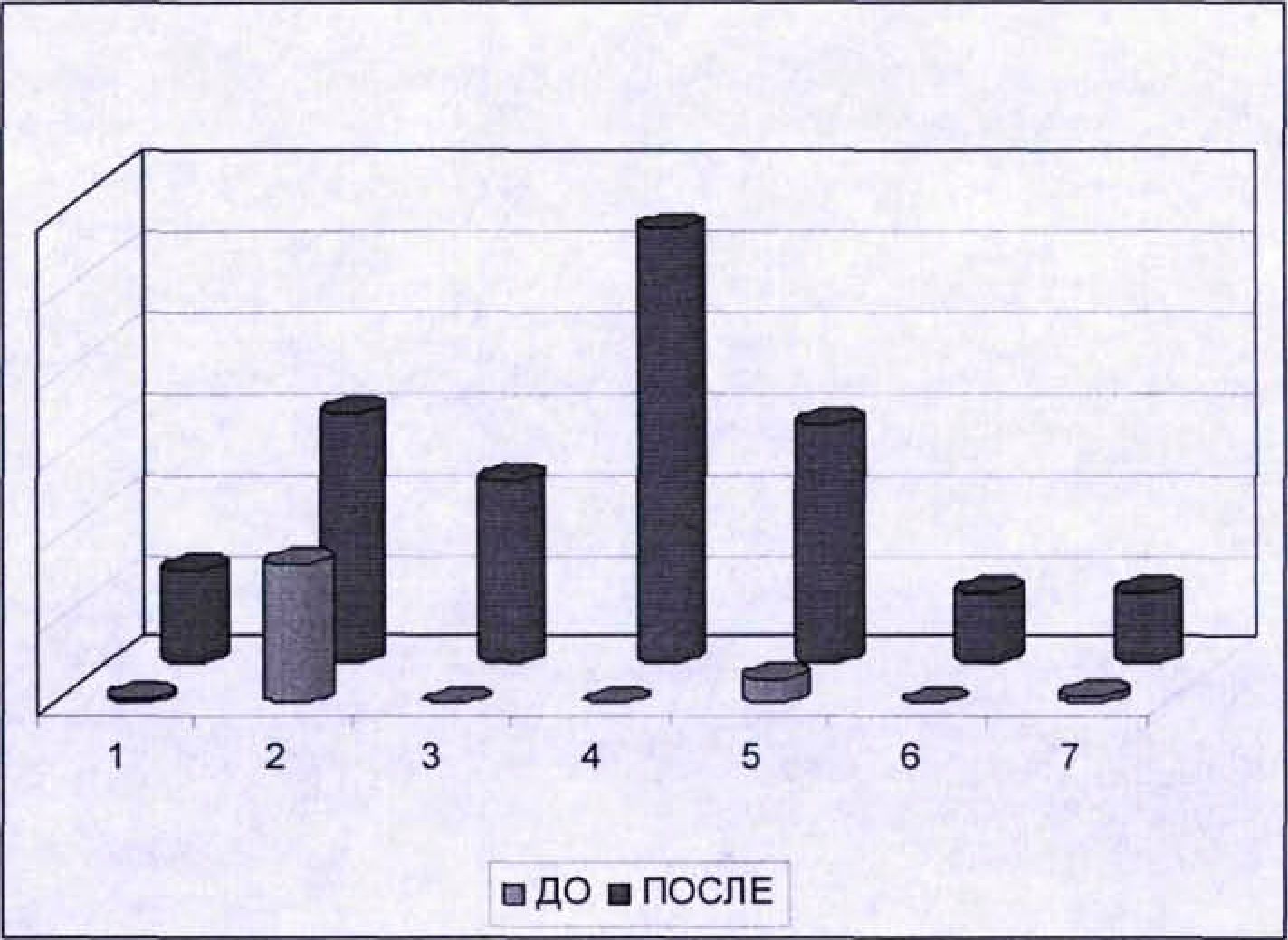
Рисунок 4.2 - Предотвращенный ущерб от 1-й угрозы
Относительная опасность (относительный ущерб) и относительная частота появления (вероятность появления) ¡-й угрозы представлены на Рисунке 4.3.
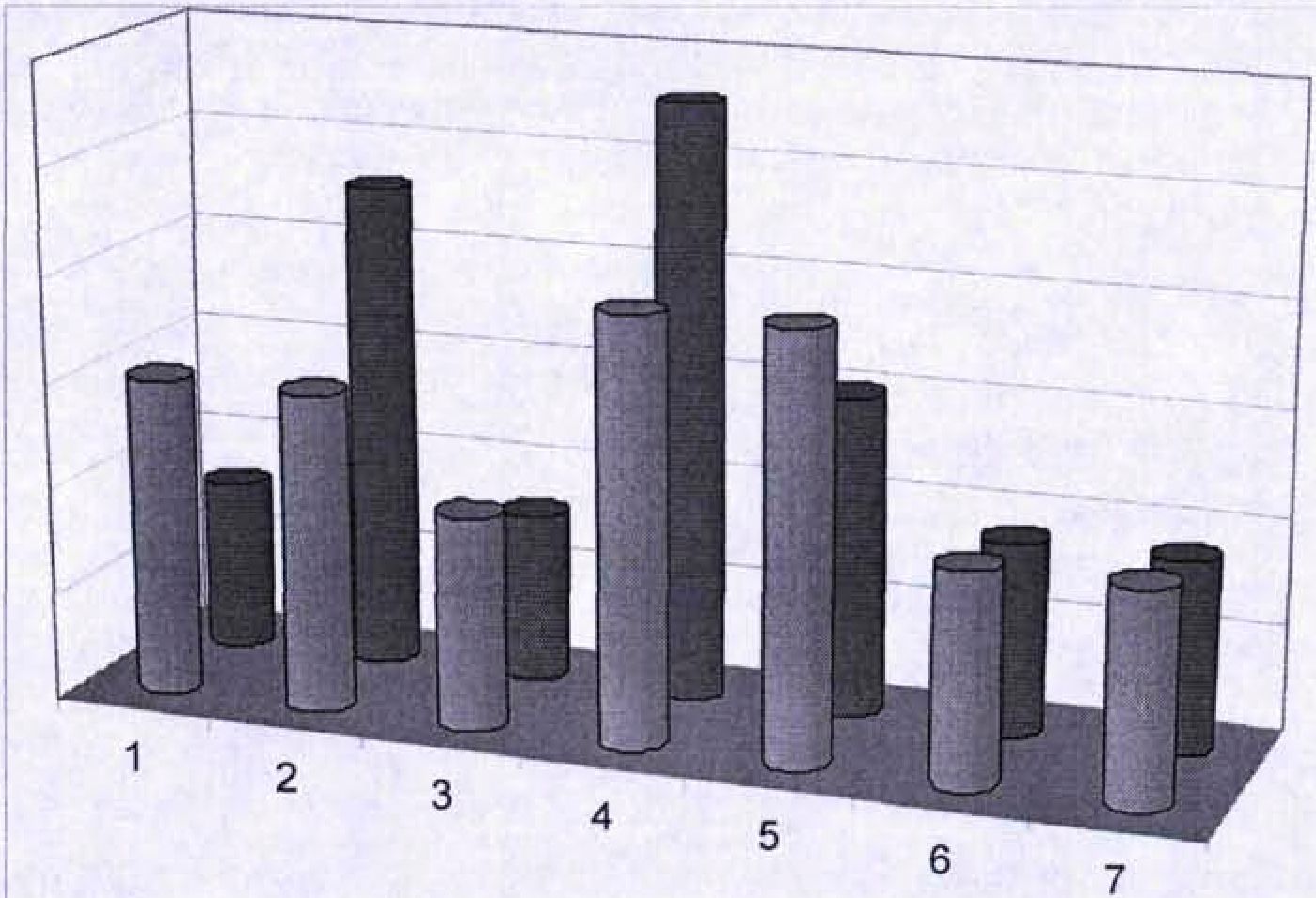
I Относительная опасность угрозы ■ Относительная частота появления
Рисунок 4.3 - Относительная опасность и относительная частота появления ¡-й угрозы
4.3 Определение важности требований, предъявляемых к СЗИ
При выборе наилучшего варианта системы защиты информации в соответствии с полученым нами критерием, возникает задача определения важности (веса) требований, предъявляемых к параметрам СЗИ.
Наиболее полный обзор методов определения коэффициентов важности приведен в литературе [98]. Иерархическая классификация методов определения коэффициентов важности требований приведена на Рисунке 4.4.
Методы определения коэффициентов важности критериев
| | Методы обработки информации в первичных шкалах | | ||||||
| 1 класс | ||||||||
| | | | | | | | ||
| Методы попарных спавненлй | | Методы точечных оценок | ||||||
| 1А класс | 1Б класс | |||||||
| | Методы обработки информации в проичводньгх шкалах | | |
| 2 класс | |||
| | | | |
| Методы аппроксимации функции полезности | Методы трансформации частот | ||
| 2А класс | 2Б класс | ||
| •атраиы | Ри гожие иетэги |
| 1А. 1 | 1А. 2 |
| | |
| 1Б. 1 | 1Б. 2 |
| М» гиды | Мг'оли $утаф1* | 'УЪ>ШМ1С1Й" | Методы травеформвиси голгш>г*<вм | М-тш тр«нс (юрмасни ътсеу'ея | Методы аагторо* СсшномиэаипА |
| 2А. 1 | 2А. 2 | 2А. 3 | 2Б. 1 | 2Б. 2 | 2Б.З |
| | три фТ*"*- | |
| 1А.2. | 1А.2. | |
| СО&ТМИШ | | |
| 1АЛ. | 1АЛ. | |
| | Мяш |
| 1Б.2Л | 1Б.2. |
| 4Н" | Мвгадм п-в | | Мвшди неЛ афтп | & | | Тгргсоую!» | вреттепВ .ТВ» |
| 2АЛ. | 2АЛ. | 2А.2. | 2А.2. | 2А.З. | 2А.З. | 2БЛ. | 2БЛ.2 |
| ХЬТвД у-ирцоко гн-.в де-рих | » пер* уа кого сноп* ил к |
| 1Б.2ЛЛ | 1Б.2Л.2 |
1А.2.2Л
1А.2.2.2
Рисунок 4.4 - Иерархическая классификация методов определения коэффициентов важности
критериев
При решении практических задач обоснования требований и оценки систем защиты информации возникает вопрос рационального выбора метода определения весовых коэффициентов из числа 19 групп изложенных в [98-102] методов. Неправильный выбор метода приводит к недостаточной обоснованности производимых операций над малодостоверными исходными экспертными данными
.
Автором решается задача выработки рекомендаций для проектировщиков АСУ ТП малой и средней сложности. Проектировщики таких АСУ ТП как правило представляют из себя малые предприятия, с числом сотрудников от 5 до 10. Решения принимает директор предприятия, реже — ведущий специалист. Поэтому главным критерием выбора метода оценки следует принимать простоту получения экспертных данных при высокой степени согласованности мнений экспертов и при минимальном количестве экспертов.
Поэтому автором проведен анализ методов определения весовых коэффициентов с целью выбора наиболее подходящих для решения задачи определения важности требований, предъявляемых к СЗИ АСУ ТП.
Анализ литературы [98, 106 и др.] позволяет определить основные факторы, влияющие на выбор метода оценки весовых коэффициентов. Рассмотрим эти факторы.
-
Физическая сущность параметров и отношение между ними.
Параметры (в нашем случае требования к СЗИ) определяются исходя из
смысла провозглашенной цели. Далее необходимо определить степень взаимосвязей между ними, т.е. зависимости или независимости. Характер зависимости или независимости (независимость по полезности, по предпочтению, по безразличию и т.д.) влияет на выбор метода оценки.
-
Сложность проведения экспертизы и трудоемкость получения экспертной информации.
Сложность и трудоемкость экспертизы определяется реальными условиями и возможностями ее проведения.
Как показано в [98], наименьшего времени общения с экспертами требует ранжирование и метод Терстоуна; метод линейной свертки требует наибольшего времени общения с экспертами (в 12 раз больше, чем ранжирование; в 2 раза больше, чем метод Черчмена-Акофа) и т.д.
-
Степень согласованности мнений экспертов.
Степень согласованности в зависит от количества привлекаемых экспертов и уровня их квалификации. В то же время на нее влияет выбранный метод оценки весов. Так, наибольшую согласованность экспертов обеспечивает линейная свертка, наименьшую - непосредственная численная оценка весов, при этом ранжирование при его простоте позволяет получить весовые коэффициенты достаточно точные и близкие к их значению, полученному методом линейной свертки.
4. Трудоемкость обработки экспертных данных.
Этот фактор не является главным при современном уровне развития вычислительной техники. Однако, применение сложных методов обработки экспертной информации может потребовать разработки специальной программы обработки, что повлияет на сроки проведения экспертизы. Очевидно, что наиболее простыми методами с этой точки зрения являются ранговые методы и балльные методы.
Учет приведенных факторов позволяет на практике выбрать рациональный вариант оценки весовых коэффициентов применительно к СЗИ АСУ ТП. Метод Саати, по мнению автора, является оптимальным по совокупности факторов для поставленной задачи.
4.3.1 Определение важности требований, предъявляемых к СЗИ, методом
Саати
Суть метода: Результаты попарного сравнения параметров описываются отношениями их весов, т.е. представимы в виде матрицы А (матрицы Саати).
А = || / Ау ||; уе1..п.
А=я2/я, 1 ... ык (43Л)
4,/я, К'К - 1
Справедливо следующее равенство [101],
(А - пЕ)'А = 0 (4.3.2)
где Е - единичная матрица; А - вектор весов
.
Для нахождения вектора весов Л необходимо решить уравнение (4.3.2). Поскольку ранг матрицы равен 1, то п — единственное собственное число этой матрицы и, следовательно, уравнение (4.3.2) имеет ненулевое решение. Более того, это единственное решение, обладающее свойством: = 1-
Это решение и есть искомый вектор относительных весов параметров — вектор Саати.
А =
1 5 1/5 1 1/6 1/4
1 ... 12 13 14 15 16 17 18 19 ... 25
6 4 1
1/7 1/6 1/4 1
Как следует из соотношения (4.3.2), необходимо решить задачу нахождения собственных значений (А - X Е) • \У = 0, где \У - собственный вектор, а А, —
126
Определим коэффициенты важности требований, предъявляемых к СЗИ АСУ ТП «ПХВ-1», на основе метода парных сравнений (метода Саати). Шкала для оценки относительной важности требований приведена в Таблице 4.4.
Таблица 4.4 - Шкала относительной важности требований
Интенсивность относительной важности
Определение
1
Равная важность сравниваемых требований
3
Умеренное (слабое) превосходство одного над другим
5
Сильное (существенное) превосходство
7
Очевидное превосходство
9
Абсолютное (подавляющее) превосходство
2,4, 6,8
Промежуточные решения между двумя соседними оценками
Основными при выборе СЗИ «ПХВ-1» являются следующие требования:
-
к аппаратным средствам защиты информации;
-
к программным средствам защиты информации;
-
к структуре АСУ ТП;
-
к нормативной базе, документации на АСУ ТП.
Определим относительную важность 4 требований к СЗИ «ПХВ-1». В результате экспертного опроса получена следующая матрица парных сравнений
:
собственное значение матрицы. Эта неоднородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы (А - X Е) равен нулю. Найдем его:
1 -Л 5 6 7
1/5 1 -Л 4 6
1/6 1/4 1-Я 4
1/7 1/6 1/4 1-Я
Уравнение имеет решение:
= 0
А, 1 = — 0,362; Х2 = -0,140+ 1,3051; X 3 =-0,140 - 1,3051; А4 = 4,390. Следовательно, X тах = 4,390. Найдем соответствующий вектор:
-4,390
5
6
7
¿У,
1/5
1 - 4,390
4
6
со2
1/6
1/4
1-4,390
4
1/7
1/6
1/4
1-4,390
б»4
Введем условие нормировки (л)1+ш2+Шз+1л)4=1. Рассмотрим систему:
- 3,390«, + 5а>2 + 6щ + 7бУ4 = 0 0,2бУ, - 3,390й>2 + 4й), + 6гу4 = 0 0,166«, + 0,25«2 - 3,390гУ3 + 4а)4 = 0 0,142«, + 0,166й>2 + 0,25й>3 -3,390й>4 =0
Система (*) имеет только нулевое решение. Для нахождения собственного вектора АЛ^ используется замена одного из уравнений (*) условием нормировки. В результате решения системы получаем собственный вектор весов: = (СО,, С02, ш3, СО4), СО] = 0,619, ш2= 0,235, 0)3= 0,101, (А)4 = 0,045.
= Л4 -4Я3 -6,914^-2,715 = О
Отметим, что матрица парных сравнений отражает согласованные суждения тогда и только тогда, когда X тах = п. Кроме того, всегда X тах > п, поэтому тах - п) дает меру несогласованности и указывает, когда суждение экспертов следует проверить. При п=4, Хтах - 4,390, мера несогласованности равна 0,390.
Индекс согласованности (ИС), который отражает качество экспертных оценок, рассчитываем по формуле: Х-п
ИС
=
ИС = (4,39 — 4) / (4 — 1) = 0,13.
Средние согласованности (СС) для матриц случайного порядка приведены в Таблице 4.5.
Таблица 4.5 - Средние согласованности для матриц случайного порядка
п
1
2
о
о
4
5
6
7
8
9
10
СС
0
0
0,58
0,90
1,12
1.24
1,32
1,41
1,45
1,49
Общая рассогласованность (ОС) рассчитывается следующим образом: ИС
ОС = —100% СС
ОС = (0,13 / 0,9) • 100% = 14,4%.
Согласно методу Саати величина ОС должна быть не более 20%, в противном случае, такие суждения экспертов следует перепроверить.
В нашем случае мера несогласованности равна 0,39 что является допустимым при принятой шкале (Таблица 4.4), показатель ОС равен 14,4%, что не превышает допустимого порога рассогласованности.
Определение весовых коэффициентов с помощью нахождения вектора XV матрицы парных сравнений является довольно трудоемкой задачей. Для решения практических задач можно [94, 97] определять весовые коэффициенты путем расчета среднего геометрического из соотношения: Гп _
Щ =н||2оу ;/ = 1.и,
11-М (4.3.3)
где а^ - коэффициенты матрицы парных сравнений.
Рассчитаем весовые коэффициенты методом среднего геометрического:
X,
х2
Х3
Х4
П*и
4л/Пху/£
X,
1
5
6
7
210
3,80
0,614
х2
0,200
1
4
6
4,8
1,48
0,239
Х3
0,166
0,250
1
4
0,166
0,64
0,103
X,
0,142
0,166
0,250
1
0,00589
0,27
0,044
1= 6,19 1,000
В нашем случае получаем: 0)1 = 0,614, С02 = 0,23 9, со3= 0,103, со4= 0,044.
Ошибки определения весовых коэффициентов не превышают 5%, что говорит о возможности применения данного метода.
В соответствии с Таблицей 4.4 мы получили сильное превосходство одного требования над другим. Это говорит о том, что есть более важные требования и мене важные. Есть явно выраженное главное требование - к аппаратным СЗИ, а также незначительное требование - к нормативной базе АСУ ТП.
Рассчитанная относительная важность требований к СЗИ АСУ ТП «ПХВ- 1» в процентах приведена в Таблице 4.6.
Таблица 4.6 - Относительная важность требований к СЗИ АСУ ТП «ПХВ-1»
Требования к СЗИ АСУ ТП
Относительная важность
к аппаратным средствам защиты информации
61,4%
к программным средствам защиты информации
23,9%
к структуре АСУ ТП
10,3%
к нормативной базе, документации на АСУ ТП
4,4%
4.4 Построение функции принадлежности
В случае если экспертная оценка имеет качественное выражение, тогда оценки вариантов по критериям и коэффициенты относительной важности задаются функциями принадлежности.
Существует значительное количество методов построения по экспертным оценкам функций принадлежности нечеткого множества ц. Л(х). Выделяют две группы методов: прямые и косвенные методы [94].
Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности ц. Л(х), характеризующей элемент х. Эти значения согласуются с его предпочтениями на множестве элементов X следующим образом:
-для любых хь х2 е X, ц. Л(Х]) < ц. л(х2) тогда и только тогда, когда х2 предпочтительнее хь т.е. в большей степени характеризуется свойством А;
- для любых хь Хг е X, р. Л(х1) = ц. л(х2) тогда и только тогда, когда X] и х2 безразличны относительно свойства А.
Примерами прямых методов являются непосредственное задание функции принадлежности таблицей, графиком или формулой. Недостатком этой группы методов является большая доля субъективизма.
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки.
Поэтому автором проанализированы косвенные методы построения функций принадлежности, из которых был отобран метод ранговых оценок. Главным преимуществом данного метода является то, что в отличие от метода парных сравнений, он не требует решения характеристического уравнения, а позволяет вычислять функции принадлежности с использованием ранговых оценок, которые достаточно легко получить при экспертном опросе. Данный метод обладает достаточной точностью вычислений и позволяет легко автоматизировать расчеты.
4.4.1 Построение функции принадлежности на основе ранговых оценок
Данный метод базируется на идее распределения степени принадлежности элементов универсального множества согласно с их рангами.
Будем понимать под рангом элемента х;еХ число г3(х]), которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом 8. Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
Введем также обозначения: г3(х^ = г;; |а5(х!) = ; I = 1 ..п.
Тогда правило распределения степеней принадлежности можно задать в виде соотношения:
Г2 г» (4.4.1)
к которому добавляется условие нормирования
:
ц, + ц2+... + цп=1 (4.4.2)
Используя соотношение (4.4.1) легко определить степени принадлежности всех элементов универсального множества через степени принадлежности опорного элемента.
Если опорным элементом является X] е X с принадлежностью ц ь то: а Л
А = — ■ А ; А = — ■■ АА, =—■ А
г1
г1
(4.4.3)
Для опорного элемента х2 е X с принадлежностью \х 2, получаем:
А = " А ^ А = " А ^ ■ ■ ■ ^ А = " А
(4.4.4)
Го Го Го
Для опорного элемента х„еХс принадлежностью ц п, имеем: г, г7 г,
М1 = --М»>М2 = --М»>-'>Мп-, = —-А
г" г» г» (4.4.5)
Учитывая условие нормировки (4.4.2) из соотношений (4.4.3) - (4.4.5) находим
:
\
г
V. >
-1
у
п
гг>
А =
ч 1
А =
, >з
/
\Г2
/
Г, А
А
(4.4.6)
Полученные формулы (4.4.6) дают возможность вычислять степени принадлежности ц 8(х;) двумя независимыми путями:
-
по абсолютным оценкам уровней г;; 1=1 ..п , которые определяются по 9- бальной шкале (1 — наименьший ранг, 9 - наибольший ранг).
-1
по относительным оценкам рангов т\/ х\ = а1} ; 1,] = 1..п, которые образуют матрицу
:
-
1 1 и
>2 Ъ
Г Г Г п ' п п
(4.4.7)
Эта матрица обладает следующими свойствами:
а) она диагональная, т.е. ан=1; ¡=Т..п;
б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: ау=1 / а^^;
в) она транзитивна, т.е. а^. ак[, поскольку
П гк _ Ъ
') О
Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы А легко определить элементы всех других строк. Если известна г-я строка, т.е. элементы а^, к; ]=1..п, то произвольный элемент щ находится так:
1 ... 13 14 15 16 17 18 19 20 ... 25
6 4 1
1/7 1/6 1/4 1
Как следует из соотношения (4.3.2), необходимо решить задачу нахождения собственных значений (А - X Е) • \У = 0, где \У - собственный вектор, а А, —
126
Определим коэффициенты важности требований, предъявляемых к СЗИ АСУ ТП «ПХВ-1», на основе метода парных сравнений (метода Саати). Шкала для оценки относительной важности требований приведена в Таблице 4.4.
Таблица 4.4 - Шкала относительной важности требований
Интенсивность относительной важности
Определение
1
Равная важность сравниваемых требований
3
Умеренное (слабое) превосходство одного над другим
5
Сильное (существенное) превосходство
7
Очевидное превосходство
9
Абсолютное (подавляющее) превосходство
2,4, 6,8
Промежуточные решения между двумя соседними оценками
Основными при выборе СЗИ «ПХВ-1» являются следующие требования:
-
к аппаратным средствам защиты информации;
-
к программным средствам защиты информации;
-
к структуре АСУ ТП;
-
к нормативной базе, документации на АСУ ТП.
Определим относительную важность 4 требований к СЗИ «ПХВ-1». В результате экспертного опроса получена следующая матрица парных сравнений
:
собственное значение матрицы. Эта неоднородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы (А - X Е) равен нулю. Найдем его:
1 -Л 5 6 7
1/5 1 -Л 4 6
1/6 1/4 1-Я 4
1/7 1/6 1/4 1-Я
Уравнение имеет решение:
= 0
А, 1 = — 0,362; Х2 = -0,140+ 1,3051; X 3 =-0,140 - 1,3051; А4 = 4,390. Следовательно, X тах = 4,390. Найдем соответствующий вектор:
-4,390
5
6
7
¿У,
1/5
1 - 4,390
4
6
со2
1/6
1/4
1-4,390
4
1/7
1/6
1/4
1-4,390
б»4
Введем условие нормировки (л)1+ш2+Шз+1л)4=1. Рассмотрим систему:
- 3,390«, + 5а>2 + 6щ + 7бУ4 = 0 0,2бУ, - 3,390й>2 + 4й), + 6гу4 = 0 0,166«, + 0,25«2 - 3,390гУ3 + 4а)4 = 0 0,142«, + 0,166й>2 + 0,25й>3 -3,390й>4 =0
Система (*) имеет только нулевое решение. Для нахождения собственного вектора АЛ^ используется замена одного из уравнений (*) условием нормировки. В результате решения системы получаем собственный вектор весов: = (СО,, С02, ш3, СО4), СО] = 0,619, ш2= 0,235, 0)3= 0,101, (А)4 = 0,045.
= Л4 -4Я3 -6,914^-2,715 = О
Отметим, что матрица парных сравнений отражает согласованные суждения тогда и только тогда, когда X тах = п. Кроме того, всегда X тах > п, поэтому тах - п) дает меру несогласованности и указывает, когда суждение экспертов следует проверить. При п=4, Хтах - 4,390, мера несогласованности равна 0,390.
Индекс согласованности (ИС), который отражает качество экспертных оценок, рассчитываем по формуле: Х-п
ИС
=
ИС = (4,39 — 4) / (4 — 1) = 0,13.
Средние согласованности (СС) для матриц случайного порядка приведены в Таблице 4.5.
Таблица 4.5 - Средние согласованности для матриц случайного порядка
п
1
2
о
о
4
5
6
7
8
9
10
СС
0
0
0,58
0,90
1,12
1.24
1,32
1,41
1,45
1,49
Общая рассогласованность (ОС) рассчитывается следующим образом: ИС
ОС = —100% СС
ОС = (0,13 / 0,9) • 100% = 14,4%.
Согласно методу Саати величина ОС должна быть не более 20%, в противном случае, такие суждения экспертов следует перепроверить.
В нашем случае мера несогласованности равна 0,39 что является допустимым при принятой шкале (Таблица 4.4), показатель ОС равен 14,4%, что не превышает допустимого порога рассогласованности.
Определение весовых коэффициентов с помощью нахождения вектора XV матрицы парных сравнений является довольно трудоемкой задачей. Для решения практических задач можно [94, 97] определять весовые коэффициенты путем расчета среднего геометрического из соотношения: Гп _
Щ =н||2оу ;/ = 1.и,
11-М (4.3.3)
где а^ - коэффициенты матрицы парных сравнений.
Рассчитаем весовые коэффициенты методом среднего геометрического:
X,
х2
Х3
Х4
П*и
4л/Пху/£
X,
1
5
6
7
210
3,80
0,614
х2
0,200
1
4
6
4,8
1,48
0,239
Х3
0,166
0,250
1
4
0,166
0,64
0,103
X,
0,142
0,166
0,250
1
0,00589
0,27
0,044
1= 6,19 1,000
В нашем случае получаем: 0)1 = 0,614, С02 = 0,23 9, со3= 0,103, со4= 0,044.
Ошибки определения весовых коэффициентов не превышают 5%, что говорит о возможности применения данного метода.
В соответствии с Таблицей 4.4 мы получили сильное превосходство одного требования над другим. Это говорит о том, что есть более важные требования и мене важные. Есть явно выраженное главное требование - к аппаратным СЗИ, а также незначительное требование - к нормативной базе АСУ ТП.
Рассчитанная относительная важность требований к СЗИ АСУ ТП «ПХВ- 1» в процентах приведена в Таблице 4.6.
Таблица 4.6 - Относительная важность требований к СЗИ АСУ ТП «ПХВ-1»
Требования к СЗИ АСУ ТП
Относительная важность
к аппаратным средствам защиты информации
61,4%
к программным средствам защиты информации
23,9%
к структуре АСУ ТП
10,3%
к нормативной базе, документации на АСУ ТП
4,4%
4.4 Построение функции принадлежности
В случае если экспертная оценка имеет качественное выражение, тогда оценки вариантов по критериям и коэффициенты относительной важности задаются функциями принадлежности.
Существует значительное количество методов построения по экспертным оценкам функций принадлежности нечеткого множества ц. Л(х). Выделяют две группы методов: прямые и косвенные методы [94].
Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности ц. Л(х), характеризующей элемент х. Эти значения согласуются с его предпочтениями на множестве элементов X следующим образом:
-для любых хь х2 е X, ц. Л(Х]) < ц. л(х2) тогда и только тогда, когда х2 предпочтительнее хь т.е. в большей степени характеризуется свойством А;
- для любых хь Хг е X, р. Л(х1) = ц. л(х2) тогда и только тогда, когда X] и х2 безразличны относительно свойства А.
Примерами прямых методов являются непосредственное задание функции принадлежности таблицей, графиком или формулой. Недостатком этой группы методов является большая доля субъективизма.
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки.
Поэтому автором проанализированы косвенные методы построения функций принадлежности, из которых был отобран метод ранговых оценок. Главным преимуществом данного метода является то, что в отличие от метода парных сравнений, он не требует решения характеристического уравнения, а позволяет вычислять функции принадлежности с использованием ранговых оценок, которые достаточно легко получить при экспертном опросе. Данный метод обладает достаточной точностью вычислений и позволяет легко автоматизировать расчеты.
4.4.1 Построение функции принадлежности на основе ранговых оценок
Данный метод базируется на идее распределения степени принадлежности элементов универсального множества согласно с их рангами.
Будем понимать под рангом элемента х;еХ число г3(х]), которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом 8. Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
Введем также обозначения: г3(х^ = г;; |а5(х!) = ; I = 1 ..п.
Тогда правило распределения степеней принадлежности можно задать в виде соотношения:
Г2 г» (4.4.1)
к которому добавляется условие нормирования
:
ц, + ц2+... + цп=1 (4.4.2)
Используя соотношение (4.4.1) легко определить степени принадлежности всех элементов универсального множества через степени принадлежности опорного элемента.
Если опорным элементом является X] е X с принадлежностью ц ь то: а Л
А = — ■ А ; А = — ■■ АА, =—■ А
г1
г1
(4.4.3)
Для опорного элемента х2 е X с принадлежностью \х 2, получаем:
А = " А ^ А = " А ^ ■ ■ ■ ^ А = " А
(4.4.4)
Го Го Го
Для опорного элемента х„еХс принадлежностью ц п, имеем: г, г7 г,
М1 = --М»>М2 = --М»>-'>Мп-, = —-А
г" г» г» (4.4.5)
Учитывая условие нормировки (4.4.2) из соотношений (4.4.3) - (4.4.5) находим
:
\
г
V. >
-1
у
п
гг>
А =
ч 1
А =
, >з
/
\Г2
/
Г, А
А
(4.4.6)
Полученные формулы (4.4.6) дают возможность вычислять степени принадлежности ц 8(х;) двумя независимыми путями:
-
по абсолютным оценкам уровней г;; 1=1 ..п , которые определяются по 9- бальной шкале (1 — наименьший ранг, 9 - наибольший ранг).
-1
по относительным оценкам рангов т\/ х\ = а1} ; 1,] = 1..п, которые образуют матрицу
:
-
1 1 и
>2 Ъ
Г Г Г п ' п п
(4.4.7)
Эта матрица обладает следующими свойствами:
а) она диагональная, т.е. ан=1; ¡=Т..п;
б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: ау=1 / а^^;
в) она транзитивна, т.е. а^. ак[, поскольку
П гк _ Ъ
') О
Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы А легко определить элементы всех других строк. Если известна г-я строка, т.е. элементы а^, к; ]=1..п, то произвольный элемент щ находится так:
1 ... 13 14 15 16 17 18 19 20 ... 25
6 4 1
1/7 1/6 1/4 1
Как следует из соотношения (4.3.2), необходимо решить задачу нахождения собственных значений (А - X Е) • \У = 0, где \У - собственный вектор, а А, —
126
Определим коэффициенты важности требований, предъявляемых к СЗИ АСУ ТП «ПХВ-1», на основе метода парных сравнений (метода Саати). Шкала для оценки относительной важности требований приведена в Таблице 4.4.
| Таблица 4.4 - Шкала относительной важности требований Интенсивность относительной важности | Определение |
| 1 | Равная важность сравниваемых требований |
| 3 | Умеренное (слабое) превосходство одного над другим |
| 5 | Сильное (существенное) превосходство |
| 7 | Очевидное превосходство |
| 9 | Абсолютное (подавляющее) превосходство |
| 2,4, 6,8 | Промежуточные решения между двумя соседними оценками |
Основными при выборе СЗИ «ПХВ-1» являются следующие требования:
-
к аппаратным средствам защиты информации; -
к программным средствам защиты информации; -
к структуре АСУ ТП; -
к нормативной базе, документации на АСУ ТП.
Определим относительную важность 4 требований к СЗИ «ПХВ-1». В результате экспертного опроса получена следующая матрица парных сравнений
:
собственное значение матрицы. Эта неоднородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы (А - X Е) равен нулю. Найдем его:
1 -Л 5 6 7
1/5 1 -Л 4 6
1/6 1/4 1-Я 4
1/7 1/6 1/4 1-Я
Уравнение имеет решение:
= 0
А, 1 = — 0,362; Х2 = -0,140+ 1,3051; X 3 =-0,140 - 1,3051; А4 = 4,390. Следовательно, X тах = 4,390. Найдем соответствующий вектор:
| -4,390 | 5 | 6 | 7 | | ¿У, |
| 1/5 | 1 - 4,390 | 4 | 6 | | со2 |
| 1/6 | 1/4 | 1-4,390 | 4 | | |
| 1/7 | 1/6 | 1/4 | 1-4,390 | | б»4 |
Введем условие нормировки (л)1+ш2+Шз+1л)4=1. Рассмотрим систему:
- 3,390«, + 5а>2 + 6щ + 7бУ4 = 0 0,2бУ, - 3,390й>2 + 4й), + 6гу4 = 0 0,166«, + 0,25«2 - 3,390гУ3 + 4а)4 = 0 0,142«, + 0,166й>2 + 0,25й>3 -3,390й>4 =0
Система (*) имеет только нулевое решение. Для нахождения собственного вектора АЛ^ используется замена одного из уравнений (*) условием нормировки. В результате решения системы получаем собственный вектор весов: = (СО,, С02, ш3, СО4), СО] = 0,619, ш2= 0,235, 0)3= 0,101, (А)4 = 0,045.
= Л4 -4Я3 -6,914^-2,715 = О
Отметим, что матрица парных сравнений отражает согласованные суждения тогда и только тогда, когда X тах = п. Кроме того, всегда X тах > п, поэтому тах - п) дает меру несогласованности и указывает, когда суждение экспертов следует проверить. При п=4, Хтах - 4,390, мера несогласованности равна 0,390.
Индекс согласованности (ИС), который отражает качество экспертных оценок, рассчитываем по формуле: Х-п
ИС
=
ИС = (4,39 — 4) / (4 — 1) = 0,13.
Средние согласованности (СС) для матриц случайного порядка приведены в Таблице 4.5.
| Таблица 4.5 - Средние согласованности для матриц случайного порядка п | 1 | 2 | о о | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| СС | 0 | 0 | 0,58 | 0,90 | 1,12 | 1.24 | 1,32 | 1,41 | 1,45 | 1,49 |
Общая рассогласованность (ОС) рассчитывается следующим образом: ИС
ОС = —100% СС
ОС = (0,13 / 0,9) • 100% = 14,4%.
Согласно методу Саати величина ОС должна быть не более 20%, в противном случае, такие суждения экспертов следует перепроверить.
В нашем случае мера несогласованности равна 0,39 что является допустимым при принятой шкале (Таблица 4.4), показатель ОС равен 14,4%, что не превышает допустимого порога рассогласованности.
Определение весовых коэффициентов с помощью нахождения вектора XV матрицы парных сравнений является довольно трудоемкой задачей. Для решения практических задач можно [94, 97] определять весовые коэффициенты путем расчета среднего геометрического из соотношения: Гп _
Щ =н||2оу ;/ = 1.и,
11-М (4.3.3)
где а^ - коэффициенты матрицы парных сравнений.
Рассчитаем весовые коэффициенты методом среднего геометрического:
| | X, | х2 | Х3 | Х4 | П*и | | 4л/Пху/£ |
| X, | 1 | 5 | 6 | 7 | 210 | 3,80 | 0,614 |
| х2 | 0,200 | 1 | 4 | 6 | 4,8 | 1,48 | 0,239 |
| Х3 | 0,166 | 0,250 | 1 | 4 | 0,166 | 0,64 | 0,103 |
| X, | 0,142 | 0,166 | 0,250 | 1 | 0,00589 | 0,27 | 0,044 |
1= 6,19 1,000
В нашем случае получаем: 0)1 = 0,614, С02 = 0,23 9, со3= 0,103, со4= 0,044.
Ошибки определения весовых коэффициентов не превышают 5%, что говорит о возможности применения данного метода.
В соответствии с Таблицей 4.4 мы получили сильное превосходство одного требования над другим. Это говорит о том, что есть более важные требования и мене важные. Есть явно выраженное главное требование - к аппаратным СЗИ, а также незначительное требование - к нормативной базе АСУ ТП.
Рассчитанная относительная важность требований к СЗИ АСУ ТП «ПХВ- 1» в процентах приведена в Таблице 4.6.
| Таблица 4.6 - Относительная важность требований к СЗИ АСУ ТП «ПХВ-1» Требования к СЗИ АСУ ТП | Относительная важность |
| к аппаратным средствам защиты информации | 61,4% |
| к программным средствам защиты информации | 23,9% |
| к структуре АСУ ТП | 10,3% |
| к нормативной базе, документации на АСУ ТП | 4,4% |
4.4 Построение функции принадлежности
В случае если экспертная оценка имеет качественное выражение, тогда оценки вариантов по критериям и коэффициенты относительной важности задаются функциями принадлежности.
Существует значительное количество методов построения по экспертным оценкам функций принадлежности нечеткого множества ц. Л(х). Выделяют две группы методов: прямые и косвенные методы [94].
Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности ц. Л(х), характеризующей элемент х. Эти значения согласуются с его предпочтениями на множестве элементов X следующим образом:
-для любых хь х2 е X, ц. Л(Х]) < ц. л(х2) тогда и только тогда, когда х2 предпочтительнее хь т.е. в большей степени характеризуется свойством А;
- для любых хь Хг е X, р. Л(х1) = ц. л(х2) тогда и только тогда, когда X] и х2 безразличны относительно свойства А.
Примерами прямых методов являются непосредственное задание функции принадлежности таблицей, графиком или формулой. Недостатком этой группы методов является большая доля субъективизма.
В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки.
Поэтому автором проанализированы косвенные методы построения функций принадлежности, из которых был отобран метод ранговых оценок. Главным преимуществом данного метода является то, что в отличие от метода парных сравнений, он не требует решения характеристического уравнения, а позволяет вычислять функции принадлежности с использованием ранговых оценок, которые достаточно легко получить при экспертном опросе. Данный метод обладает достаточной точностью вычислений и позволяет легко автоматизировать расчеты.
4.4.1 Построение функции принадлежности на основе ранговых оценок
Данный метод базируется на идее распределения степени принадлежности элементов универсального множества согласно с их рангами.
Будем понимать под рангом элемента х;еХ число г3(х]), которое характеризует значимость этого элемента в формировании свойства, которое описывается нечетким термом 8. Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
Введем также обозначения: г3(х^ = г;; |а5(х!) = ; I = 1 ..п.
Тогда правило распределения степеней принадлежности можно задать в виде соотношения:
Г2 г» (4.4.1)
к которому добавляется условие нормирования
:
ц, + ц2+... + цп=1 (4.4.2)
Используя соотношение (4.4.1) легко определить степени принадлежности всех элементов универсального множества через степени принадлежности опорного элемента.
Если опорным элементом является X] е X с принадлежностью ц ь то: а Л
А = — ■ А ; А = — ■■ АА, =—■ А
г1
г1
(4.4.3)
Для опорного элемента х2 е X с принадлежностью \х 2, получаем:
А = " А ^ А = " А ^ ■ ■ ■ ^ А = " А
(4.4.4)
Го Го Го
Для опорного элемента х„еХс принадлежностью ц п, имеем: г, г7 г,
М1 = --М»>М2 = --М»>-'>Мп-, = —-А
г" г» г» (4.4.5)
Учитывая условие нормировки (4.4.2) из соотношений (4.4.3) - (4.4.5) находим
:
| | \ |
| г | |
| | |
| V. > | -1 |
| у | |
| п | |
| гг> | |
А =
ч 1
А =
, >з
/
\Г2
/
Г, А
А
(4.4.6)
Полученные формулы (4.4.6) дают возможность вычислять степени принадлежности ц 8(х;) двумя независимыми путями:
-
по абсолютным оценкам уровней г;; 1=1 ..п , которые определяются по 9- бальной шкале (1 — наименьший ранг, 9 - наибольший ранг).
-1
по относительным оценкам рангов т\/ х\ = а1} ; 1,] = 1..п, которые образуют матрицу
:
1 1 и
>2 Ъ
Г Г Г п ' п п
(4.4.7)
Эта матрица обладает следующими свойствами:
а) она диагональная, т.е. ан=1; ¡=Т..п;
б) элементы, которые симметричны относительно главной диагонали, связаны зависимостью: ау=1 / а^^;
в) она транзитивна, т.е. а^. ак[, поскольку
П гк _ Ъ
') О
Наличие этих свойств приводит к тому, что при известных элементах одной строки матрицы А легко определить элементы всех других строк. Если известна г-я строка, т.е. элементы а^, к; ]=1..п, то произвольный элемент щ находится так:
1 ... 13 14 15 16 17 18 19 20 ... 25