ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 453
Скачиваний: 1
СОДЕРЖАНИЕ
1. Составляющие информационной технологии
2. Инструментарий информационной технологии
3. Виды современных информационных технологий
4. Проблемы и перспективы использования информационных технологий
Текстовый редакторMicrosoft Word 2003
Лабораторные задания поMicrosoftWord Ввод и форматировние текста
Признак деления - вид задач и процессов обработки информации
Признак деления — проблемы, стоящие на пути информатизации общества
Глава 1. Планирование эксперимента
Особенности планирования эксперимента
Выбор оптимальных условий эксперимента
Глава 3. Оптимальная структура моделей
Глава 1. Аппроксимация функций
Табличный процессор Microsoft Excel 2003
Лабораторные задания поMicrosoftExcel Оформление таблиц
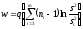 ,
где
,
где
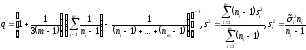
Для подтверждения (или опровержения) гипотезы при заданном уровне значимости находиться правосторонняя критическая точка wкр, определяющая критический интервал (wкр;+). Если w попадает в интервал, то гипотеза H0: 21=22=…=2m отвергается, иначе принимается.
Если гипотеза H0: 21=22=…=2m подтверждается, то можно приступить к процедуре дисперсионного анализа, т.е. проверке гипотезы H0: а1=а2=…=аm.
В
математической статистике доказывается
формула:
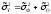 ,
где
,
где
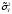 -
общая
выборочная дисперсия,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А и остаточных факторов;
-
общая
выборочная дисперсия,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А и остаточных факторов;
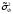 -
дисперсия
групповых средних,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А;
-
дисперсия
групповых средних,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А;
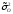 -
средняя
групповых дисперсий,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
остаточных факторов.
-
средняя
групповых дисперсий,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
остаточных факторов.
В математической статистике доказывается, что если гипотеза H0: а1=а2=…=аm верна, то величина
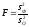
имеет F-распределение с числом степеней свободы k=m-1 и l=n-m.
При использовании F-критерия строиться правосторонняя критическая область (Fкр;+). Если расчетное значение Fр- попадает в интервал, то гипотеза H0: а1=а2=…=аm отвергается, т.е. считается что фактор А влияет на результативный признак Y, иначе влияние фактора А на признак Y не подтверждается.
Режим «Однофакторный дисперсионный анализ» служит для выяснения факта влияния контролируемого фактора А на результативный признак Y на основе выборочных данных.
Команда Сервис/Анализ данных/Однофакторный дисперсионный анализ отображает диалоговое окно, в котором задаются параметры, указанные в таблице 14.
|
Параметр |
Описание |
|
Группирование |
Устанавливается в положение «По столбцам», «По строкам» в зависимости от расположения данных во входном диапазоне |
|
Альфа |
См. описание в режиме «Двухвыборочный t-тест» таб. 13 |
|
Входной интервал |
См. описание в режиме «Гистограмма» таб. 10 |
|
Метки |
|
|
Выходной интервал |
|
|
Новый рабочий лист |
|
|
Новая рабочая книга |
Таблица 14. Параметры режима «Однофакторный дисперсионный анализ»
На рис. 49 приведен пример использования режима «Однофакторный дисперсионный анализ». Известны данные об объеме работ, выполненных на стройке (за смену) четырьмя бригадами. Требуется выяснить, зависит ли объем выполненных работ от работающей бригады при уровне значимости =0,05.
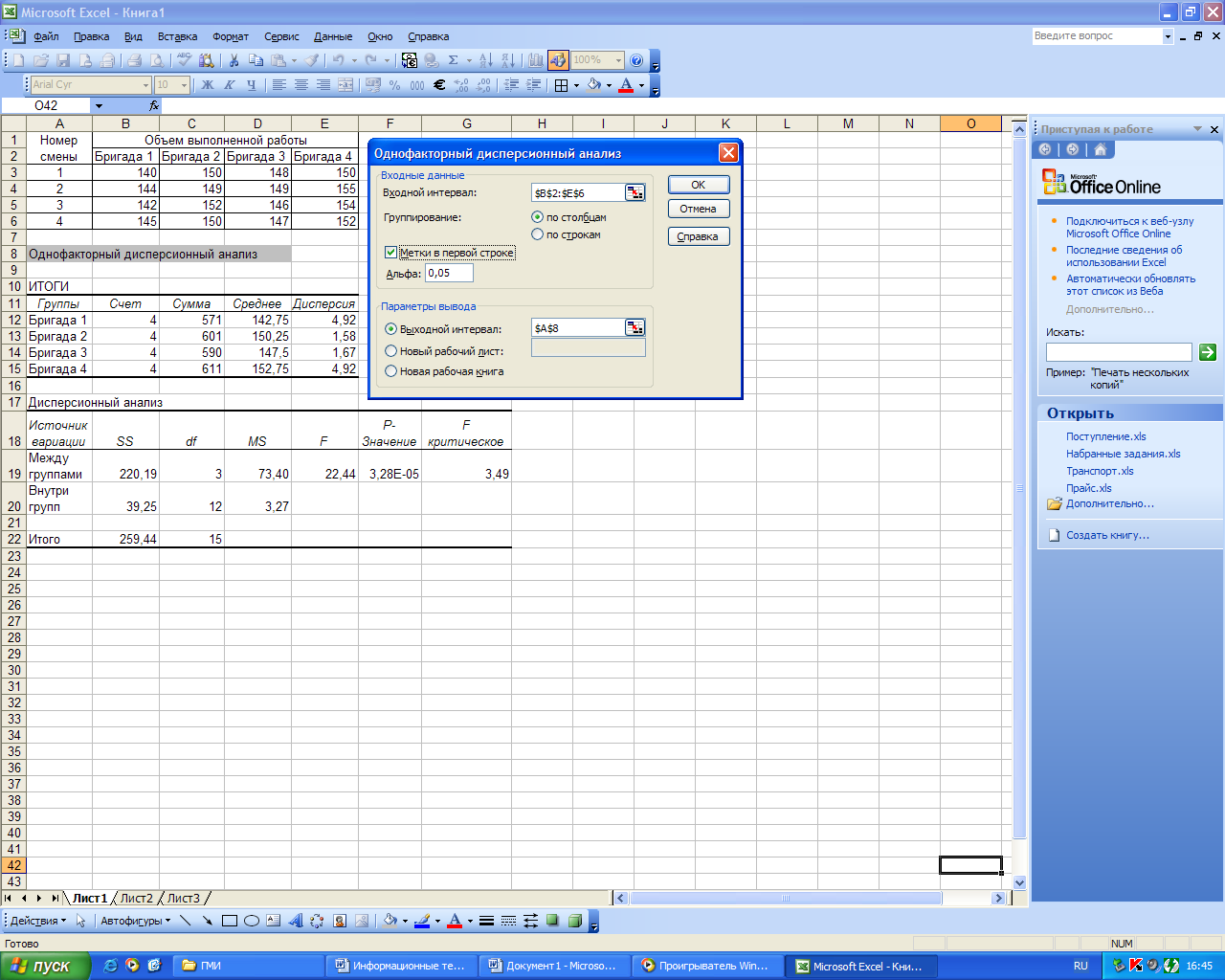
Рисунок 50. Пример использования режима «Однофакторный дисперсионный анализ»
Так как Fр попадает в критическую область, то можно сделать вывод о том, что объем ежедневной выработки зависит от работающей бригады.
Двухфакторный дисперсионный анализ без повторений и с повторениями
Логика однофакторного и двухфакторного дисперсионного анализа во многом схожа, разница состоит в наличии двух факторов А и В, т.е. проверке следующих гипотез:
HА: а1=а2=…=аmА;
HВ: b1=b2=…=bmВ.
Основой
проведения двухфакторного дисперсионного
анализа служит комбинационная группировка
по двум факторам с последующим разложением
дисперсии результативного признака
по формуле
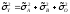 ,
где
,
где
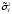 -
общая
выборочная дисперсия,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А, фактора В и остаточных
факторов;
-
общая
выборочная дисперсия,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А, фактора В и остаточных
факторов;
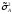 -
дисперсия
групповых средних по фактору А,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А;
-
дисперсия
групповых средних по фактору А,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора А;
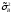 -
дисперсия
групповых средних по фактору В,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора В;
-
дисперсия
групповых средних по фактору В,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
фактора В;
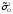 -
средняя
групповых дисперсий,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
остаточных факторов.
-
средняя
групповых дисперсий,
показатель вариации наблюдаемых
«игреков», вызванной влиянием на Y
остаточных факторов.
На
основе данного разложения для генеральной
дисперсии 2
находятся четыре несмещенные оценки
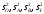 .
Причем оценка
.
Причем оценка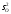 является несмещенной в любом случае,
оценка
является несмещенной в любом случае,
оценка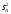 - при выполнении гипотезы НА,
оценка
- при выполнении гипотезы НА,
оценка
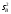 -
при выполнении гипотезы Нв,
а оценка
-
при выполнении гипотезы Нв,
а оценка
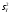 - при выполнении гипотезы НА
и Нв.
- при выполнении гипотезы НА
и Нв.
В математической статистике доказывается, что если гипотеза HА верна, то величина
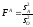
Имеет F-распределение с числом степеней свободы k=mA-1 и l=(mA-1)(mB-1).
Аналогично рассчитывается FB. Проверка выдвинутых гипотез осуществляется так же, как и при однофакторном дисперсионном анализе.
Двухфакторный дисперсионный анализ имеет две разновидности: без повторений и с повторениями. В первом случае каждому уровню факторов соответствует только одна выборка данных, во втором – определенным уровням может соответствовать более одной выборки.
Режимы «Двухфакторный дисперсионный анализ без повторений» и «Двухфакторный дисперсионный анализ с повторениями» служат для выяснения на основе выборочных данных факта влияния контролируемого факторов А и В на результативный признак Y. При этом в режиме «Двухфакторный дисперсионный анализ без повторений» каждому уровню А и В соответствует только одна выборка данных, а в режиме «Двухфакторный дисперсионный анализ с повторениями» каждому уровню одного из факторов А (или В) соответствует более одной выборки данных. В последнем случае число выборок для каждого уровня должно быть одинаковым.
Команда Сервис/Анализ данных/Двухфакторный дисперсионный анализ без повторений (с повторениями) отображает диалоговое окно, в котором задаются те же параметры, что указаны в таблице 14, только добавлено поле Число строк для выборки, в которое вводиться число выборок, приходящихся на каждый уровень одного из факторов.
На рис. 50 приведен пример использования режима «Двухфакторный дисперсионный анализ без повторений». Известны данные о разрывной нагрузке пряжи на разных станках и из разного сырья. Требуется при уровне значимости =0,05 выяснить, влияют ли на качество пряжи, измеряемое величиной разрывной нагрузки, тип станка и вид сырья.
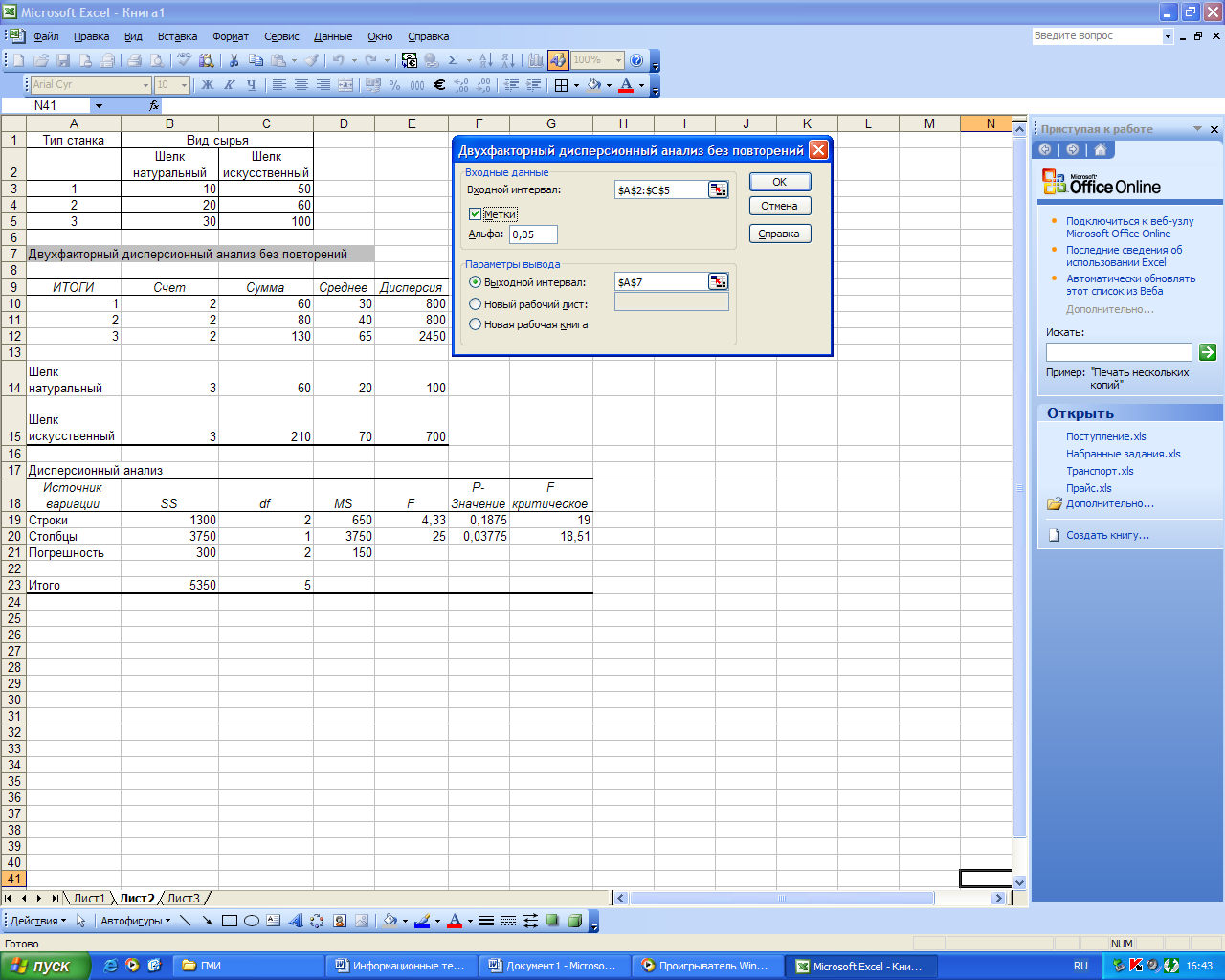
Рисунок 51. Пример использования режима «Двухфакторный дисперсионный анализ без повторений»
Расчетное значение F-критерия фактора А (тип станка) равное 4,33 не попадает в правосторонний интервал (19, +), следовательно считаем, что влияние станков на качество пряжи не подтвердилось. А расчетное значение F-критерия фактора В, равное 25 попадает в критическую область (18,51; +), следовательно вид сырья влияет на качество пряжи.
На рис. 51 приведен пример использования режима «Двухфакторный дисперсионный анализ с повторениями». Известны данные об урожайности пшеницы, выращенной на участках, на которых вносились различные виды удобрений и которые подвергались различной химической обработке. Требуется при уровне значимости =0,05 выяснить, влияют ли на урожайность пшеницы вид удобрения и способ химической почвы.
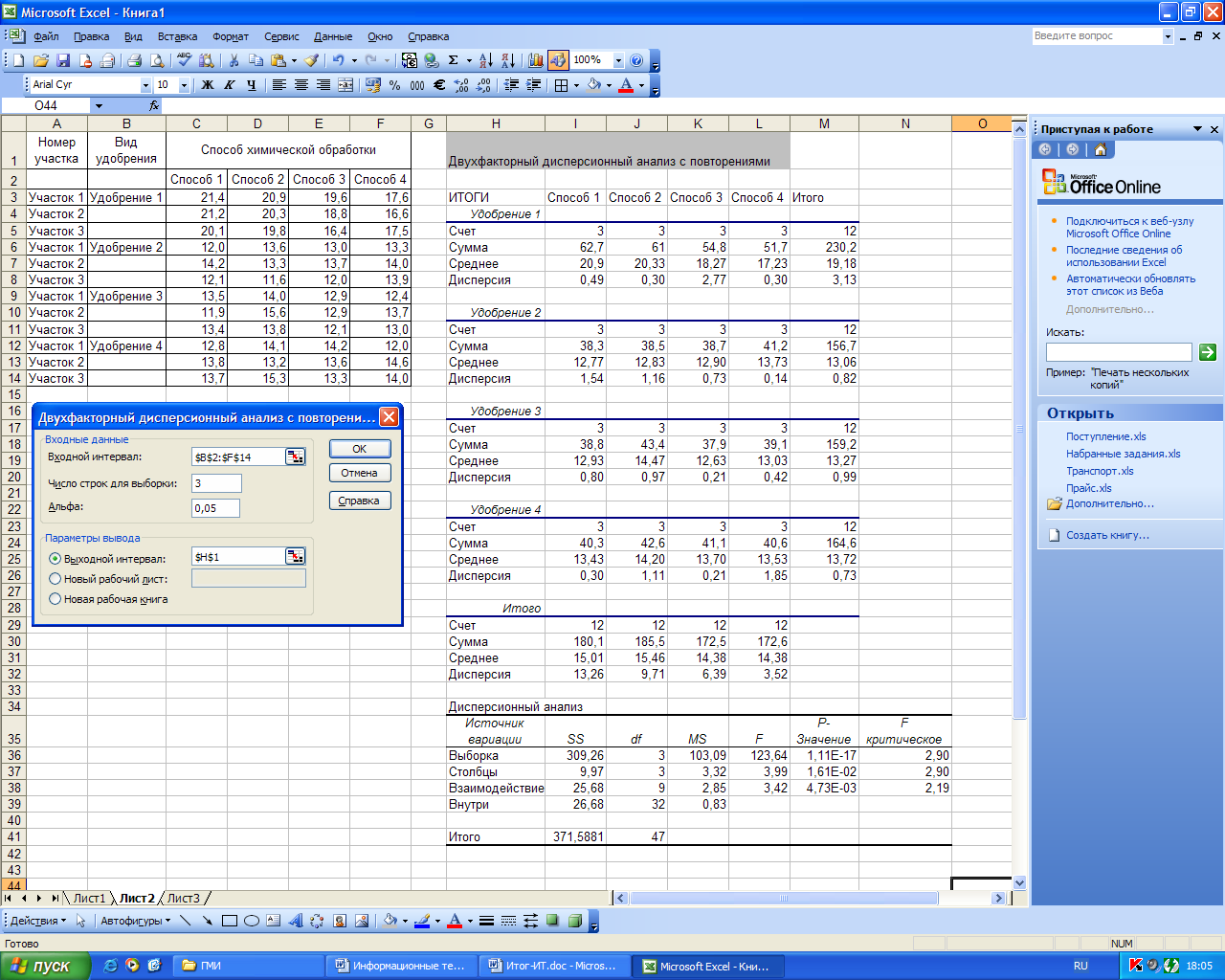
Рисунок 52. Пример использования режима «Двухфакторный дисперсионный анализ с повторениями»
Так как расчетное значение F-критерия фактора А (вид удобрения) равное 123,64 попадает в критическую область (2,9; +), то считаем, что вид удобрения влияет на урожайность. И расчетное значение F-критерия фактора В, равное 3,99 попадает в критическую область (2,9; +), следовательно способ химической обработки так же влияет на урожайность пшеницы.
Лабораторные задания поMicrosoftExcel Оформление таблиц
Задание 1.
Создать таблицу «Приходный ордер» и оформить по образцу
Задание 2.
Создать таблицу «Расчетная ведомость». Оформление осуществить в соответствии я заданиями в таблицах «Шрифт», Выравнивание», «Цвет», «Формат»
|
Дата |
Ставка рефинансирования |
Процентная ставка |
Сумма |
Начислено процентов |
Кол-во дней займа |
Доход |
Налог |
||||||||||
|
получения |
возврата |
займа |
процентов |
||||||||||||||
|
20.02.2005 |
21.05.2005 |
24% |
10% |
50 000 |
|
|
|
|
|
||||||||
|
05.01.2005 |
01.03.2005 |
28% |
5% |
9 000 |
|
|
|
|
|
||||||||
|
01.02.2005 |
05.03.2005 |
28% |
5% |
6 000 |
|
|
|
|
|
||||||||
|
01.04.2005 |
05.06.2005 |
25% |
8% |
10 000 |
|
|
|
|
|
||||||||
|
05.03.2005 |
09.04.2005 |
28% |
5% |
4 000 |
|
|
|
|
|
||||||||
|
ИТОГО |
1 238 |
432 |
|||||||||||||||