Файл: Информационные технологии-Багиева.docx

Рисунок 45. Кумулята для интервального ряда распределения

Режим «Гистограмма» служит для вычисления частот попадания данных в указанные границы интервального вариационного ряда распределения.

Команда Сервис/Анализ данных/Гистограмма отображает диалоговое окно (рис. 45), в котором задаются параметры, указанные в таблице 10.

Таблица 10. Параметры режима «Гистограмма»

На рис. 45 приведен пример построения гистограммы и кумуляты, для задачи, в которой представлен общий объем товарооборота по районам Ярославский области.

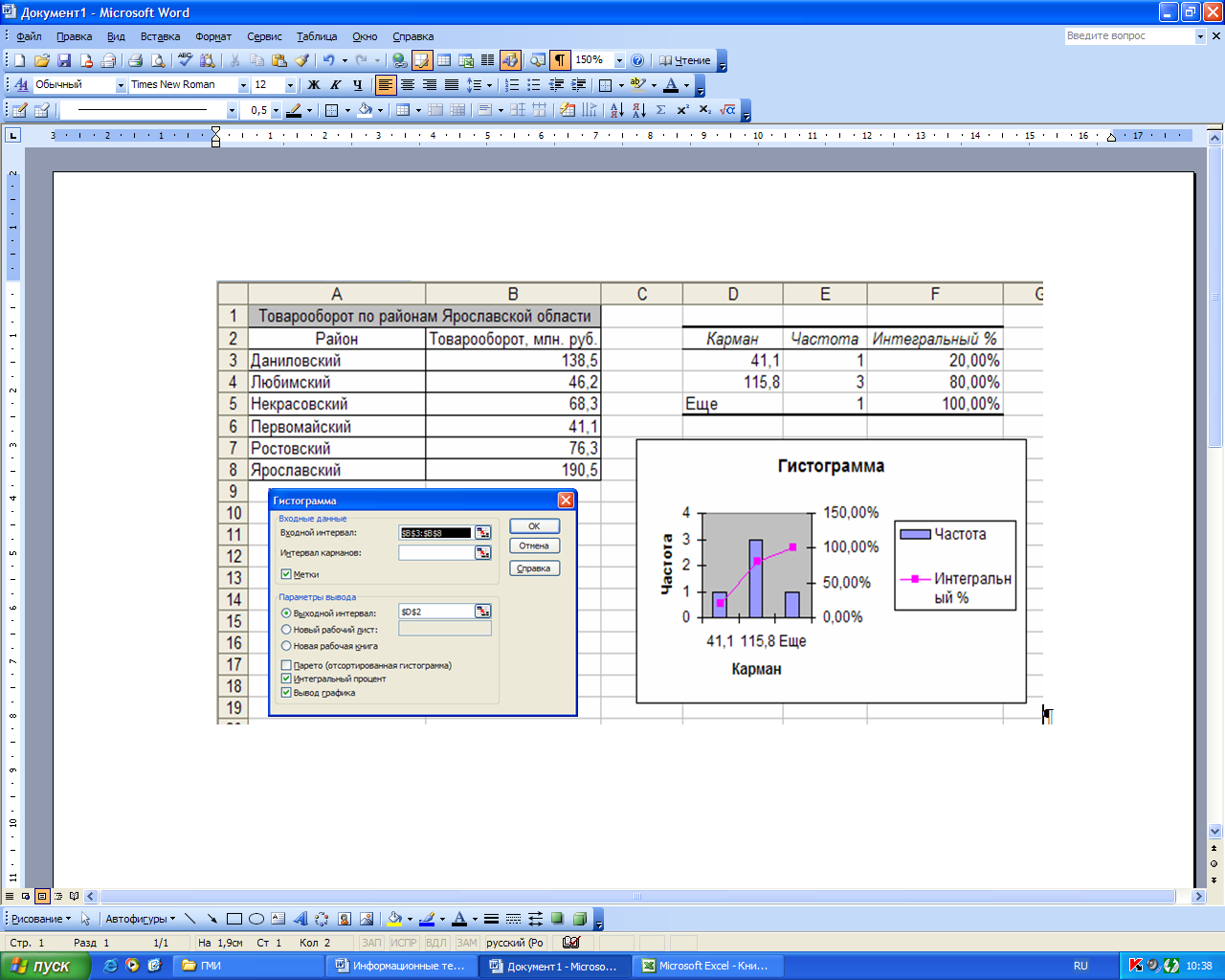
Рисунок 46. Пример построения гистограммы и кумуляты

Выборка

Исследование массовых статистических явлений в зависимости от полноты охвата изучаемого объекта бывает сплошным и несплошным (выборочным). Под выборочным наблюдением понимается метод исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. Выборка должна быть представительной (репрезентативной), чтобы по ней можно было судить о генеральной совокупности. Выборочный метод позволяет значительно сократить время на контроль и получение основных статистических характеристик, но может привести и к появлению ошибок, уменьшающих получение истинных характеристик генеральной совокупности. Данное обстоятельство важно учитывать при формировании малых выборок. Достаточно сложной проблемой является определение оптимального объема выборки. В математической статистике доказывается, что необходимая численность собственно-случайной повторной выборки определяется выражением:

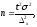
где ∆_х – предельная ошибка выборки;

² – дисперсия генеральной совокупности;

t – коэффициент доверия.

Режим «Выборка» служит для формирования выборки из генеральной совокупности на основе механизма повторного собственно-случайного отбора, а также из периодических данных.

Команда Сервис/Анализ данных/Выборка отображает диалоговое окно, в котором задаются параметры, указанные в таблице 11.

Таблица 11. Параметры режима «Выборка»

На рис. 46 приведен пример использования режима «Выборка», для организации лотереи. Требуется отобрать три победителя.

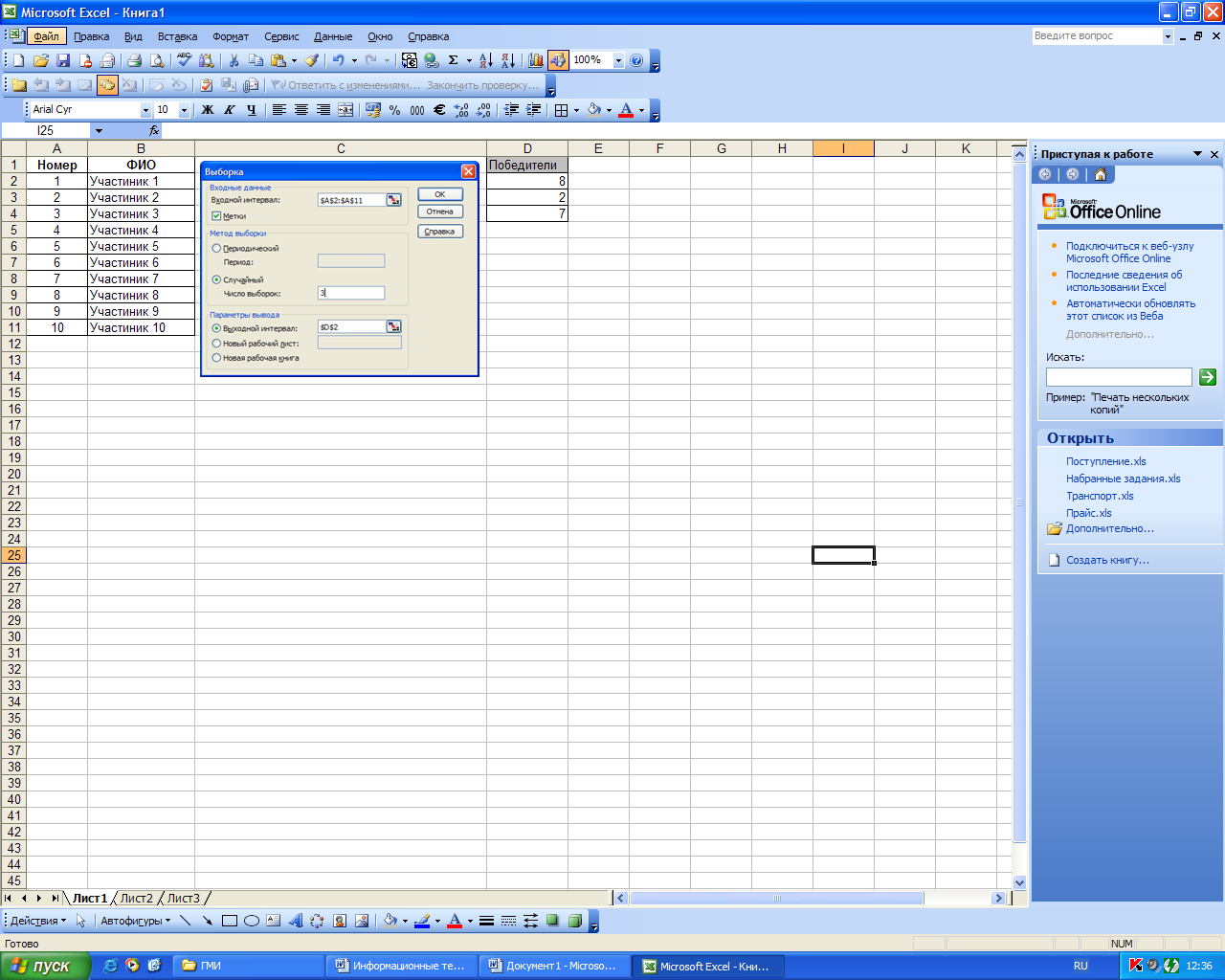
Рисунок 47. Пример использования режима «Выборка»

Генерация случайных чисел

Случайной называется переменная величина, принимающая в зависимости от случая те или иные значения с определенными вероятностями. Чтобы дать полное математическое описание случайной величины, нужно указать множество ее значений и соответствующие случайной величине распределение вероятностей на этом множестве. Для дискретной случайной величины используется статистический ряд распределения, для непрерывной случайной величины используется функция распределения. Функцией распределения случайной величины Х называется функция F(x), задающая вероятность того, что случайная величина Х принимает значение, меньшее х, т.е. F(x)=P(X<x).

В статистике широко используются различные виды теоретических распределений – нормальное распределение, биноминальное, дискретное, распределение Пуассона и т.д.

Режим «Генерация случайных чисел» служит для формирования массива случайных чисел, распределенных по одному из теоретических распределений. В зависимости от выбранного теоретического распределения меняются параметры диалогового окна «Генерация случайных чисел». Общими параметрами являются параметры, указанные в таблице 12.

Таблица 12. Параметры режима «Генерация случайных чисел»

На рис. 47 приведен пример использования режима «Генерация случайных чисел», если требуется смоделировать 10 подбрасываний двух игральных костей. Предварительно следует сформировать таблицу значений и вероятностей, а затем задать соответствующие параметры в диалоговом окне. Заметим, что для дискретного распределения сумма вероятностей должна быть равна 1.

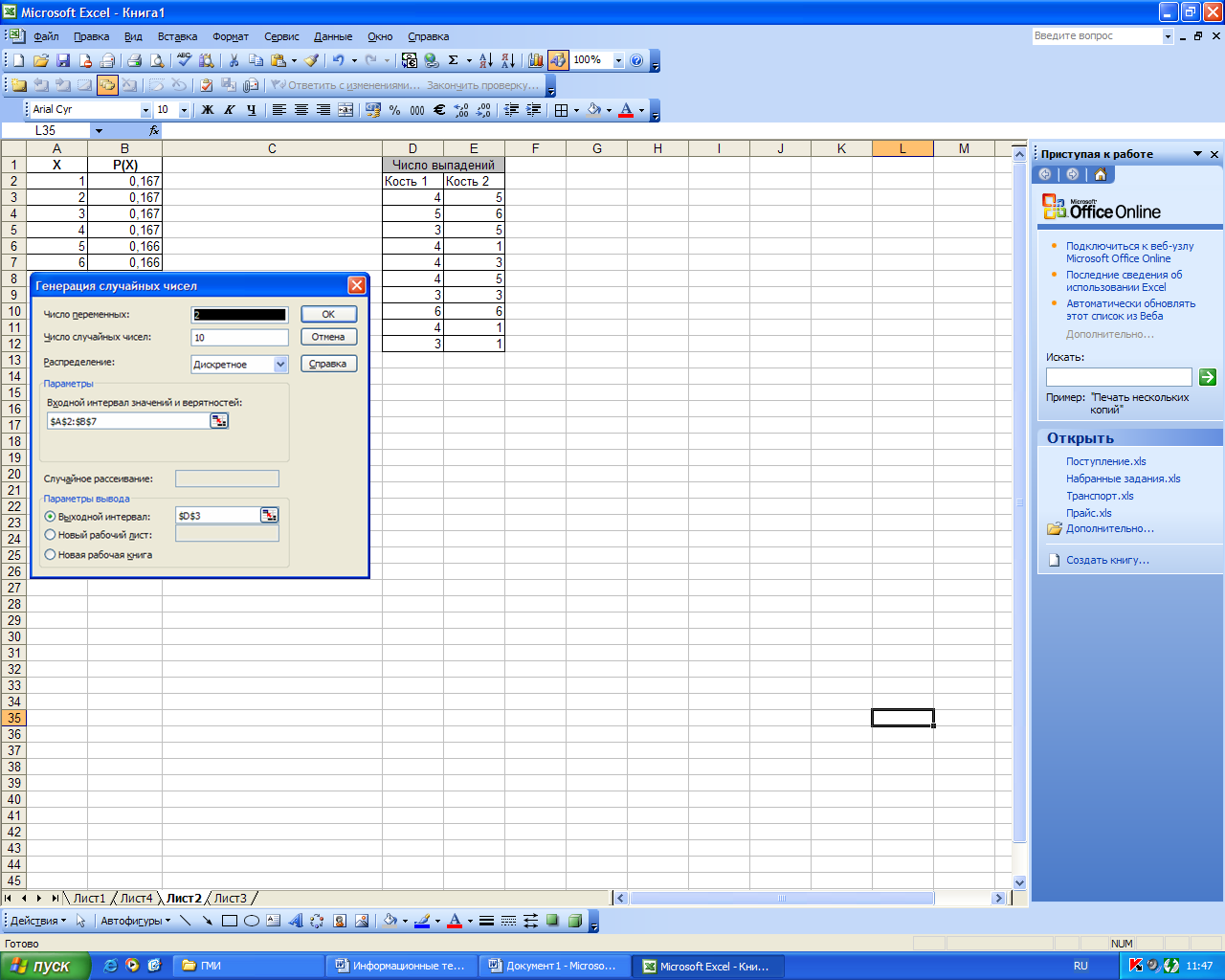
Рисунок 48. Пример использования режима «Генерация случайных чисел»

Двухвыборочный t-тест с одинаковыми и различными дисперсиями

Режим «Двухвыборочный t-тест с одинаковыми (различными) дисперсиями» служит для проверки гипотез о различии между средними (математическими ожиданиями) двух нормальных распределений соответственно с неизвестными, но равными дисперсиями (²_х=²_у) и с неизвестными дисперсиями, равенство которых не предполагается.

Команда Сервис/Анализ данных/Двухвыборочный t-тест с одинаковыми дисперсиями (Двухвыборочный t-тест с различными дисперсиями) отображает диалоговое окно, в котором задаются параметры, указанные в таблице 13.

Таблица 13. Параметры режима «Двухвыборочный t-тест с одинаковыми (различными) дисперсиями»

На рис. 48 приведен пример использования режима «Двухвыборочный t-тест с одинаковыми (различными) дисперсиями». Известны данные о расходе сырья при производстве продукции по старой и новой технологиям. Требуется проверить гипотезу H₀: a_x=a_y , предположив, что =0,05,соответствующие генеральные совокупности имеют нормальное распределения:

1. с одинаковыми дисперсиями;

2. с различными дисперсиями.

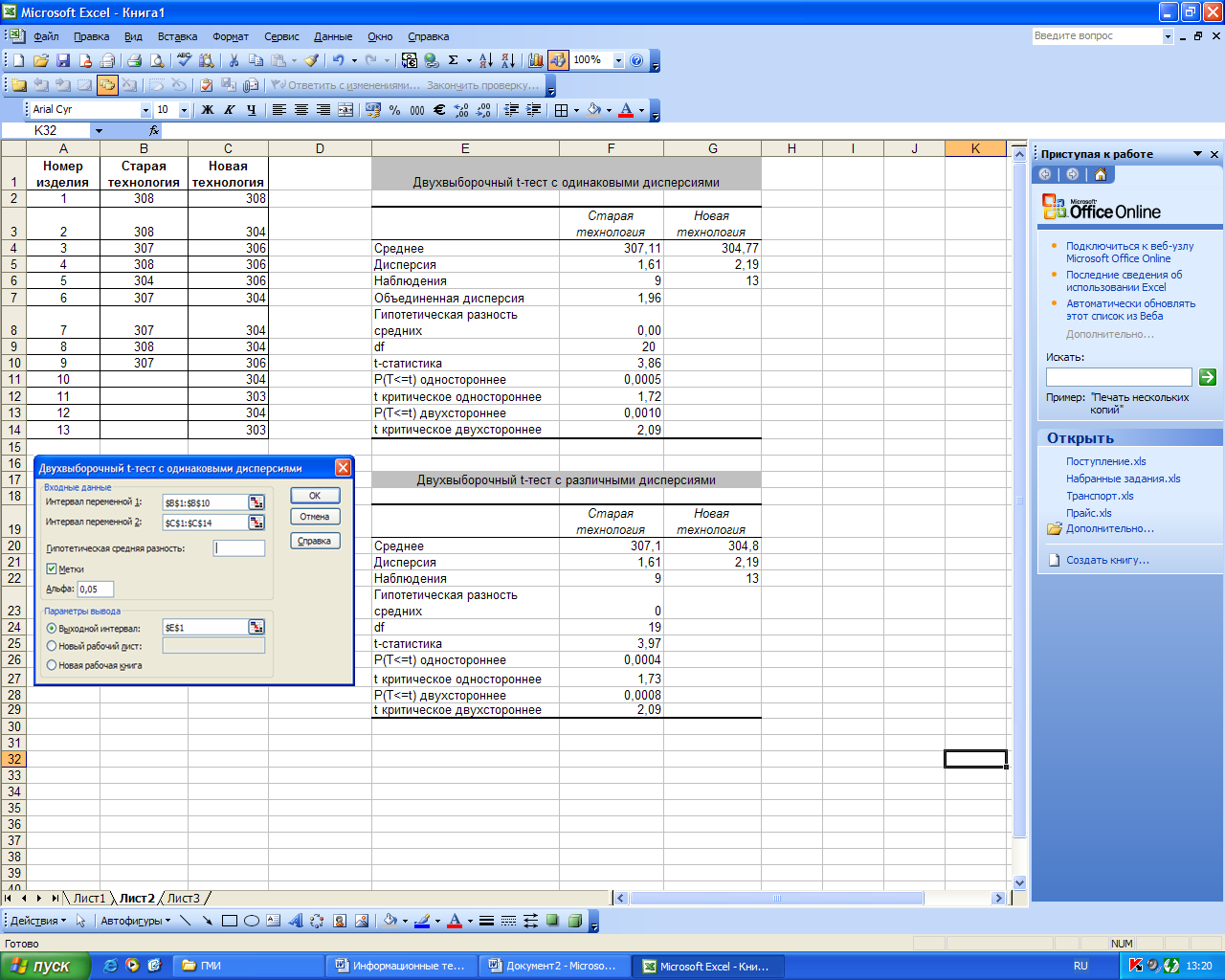
Рисунок 49. Пример использования режима «Двухвыборочный t-тест с одинаковыми (различными) дисперсиями»

Дисперсионный анализ

Дисперсионный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных одновременно действующих факторов и оценка их влияния. В зависимости от количества факторов, включенных в анализ, различают классификацию по одному фактору (однофакторный анализ), по двум признакам (двухфакторный анализ) и многофакторную классификацию, изучением которой занимается многофакторный анализ.

Задачи однофакторного дисперсионного анализа являются самыми простыми, но часто встречаются на практике. Методы дисперсионного анализа основываются на следующем: пусть а₁, а₂, …, а_m – математическое ожидание результатов признака соответственно при уровне А⁽¹⁾, А⁽²⁾, …, А^(m) (i=1,2, , m). Если при изменении уровня фактора групповые математические ожидания не изменяются, т.е. а₁= а₂ =…= а_m, то считают, что результативный признак не зависит от фактора А, в противном случае такая зависимость имеется. Поскольку числовые значения математических ожиданий неизвестны, возникает задача проверки гипотезы H₀: а₁=а₂=…=а_m, при выполнении условий:

1. наблюдения независимы и проводятся в одинаковых условиях;

2. результативный признак имеет нормальное распределение с постоянной для различных уровней генеральной дисперсией ².

Для проверки гипотезы о равенстве дисперсий трех (и более) нормальных распределений применяется критерий Бартлетта.