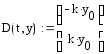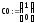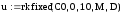ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 93
Скачиваний: 0
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка График Ю 3D Точечный, причем поверхность задается параметрически - с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).
CreateSpace (F , t0, t1, tgrid, fmap)
Возвращает вложенный массив трех векторов, представляющих х-, у-, и z-координаты пространственной кривой, определенной функцией F. t0 и t1 - диапазон изменения переменной, tgrid - размер сетки переменной, fmap - функция отображения. Все параметры, за исключением F, - факультативные.
Особый интерес представляет собой возможность построения на одном графике ряда разных фигур или поверхностей с автоматическим учетом их взаимного пересечения. Для этого надо раздельно задать матрицы соответствующих поверхностей и после вывода шаблона 3D-графика перечислить эти матрицы под ним с использованием в качестве разделителя запятой (Рисунок 4).
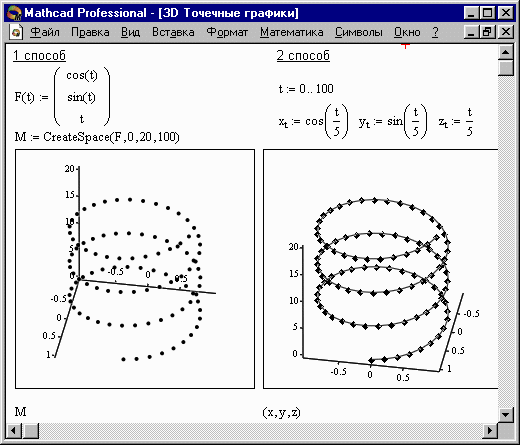
Рисунок 3.
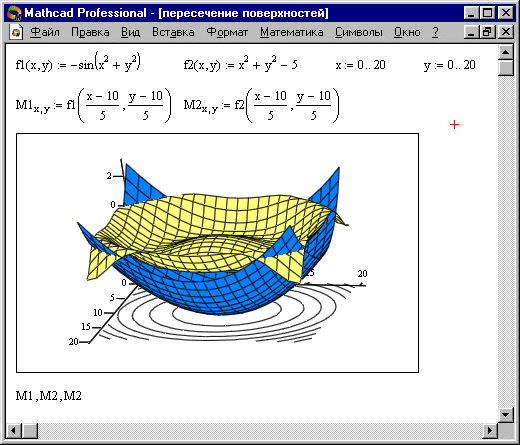
Рисунок 4.
Лабораторная работа №2
МОДЕЛИРОВАНИЕ КИНЕТИКИ ХИМИЧЕСКИХ РЕАКЦИЙ
Цель работы: получение навыков построения математических моделей необратимых химических реакций
1. Теоретические положения
Реакция называется простой, если скорость образования (расходования) вещества Сi зависит от концентраций только исходных веществ. Принятые или истинные механизмы простых реакций учитывают только один путь химического превращения.
Если в простой реакции
участвует n
веществ
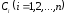 ,
то материальный баланс реакции выражается
уравнением:
,
то материальный баланс реакции выражается
уравнением:
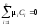 ,
(1.1)
,
(1.1)
где
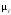 -
стехиометрические коэффициенты
(отрицательные для исходных и положительные
для образующихся веществ).
-
стехиометрические коэффициенты
(отрицательные для исходных и положительные
для образующихся веществ).
Коэффициент
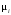 показывает, сколько молекул вещества
Сi
участвует в реакции. Изменение концентрации
вещества
показывает, сколько молекул вещества
Сi
участвует в реакции. Изменение концентрации
вещества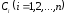 в простой реакции описывается
дифференциальным уравнением:
в простой реакции описывается
дифференциальным уравнением:
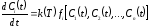 .
(1.2)
.
(1.2)
Функция
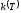 называется константой скорости реакции
и чаще всего задается уравнением
Аррениуса:
называется константой скорости реакции
и чаще всего задается уравнением
Аррениуса:
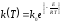 ,
(1.3)
,
(1.3)
где
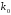 - предэкпоненциальный множитель,
характеризующий вероятность взаимодействия
молекул веществ, энергия которых
достаточна для осуществления реакции;
Е
– энергия активации, равная избытку
энергии относительно средней энергии
молекул при данной температуре, которым
должны обладать молекулы веществ для
осуществления химического взаимодействия;
R
- универсальная газовая постоянная; Т
– абсолютная температура.
- предэкпоненциальный множитель,
характеризующий вероятность взаимодействия
молекул веществ, энергия которых
достаточна для осуществления реакции;
Е
– энергия активации, равная избытку
энергии относительно средней энергии
молекул при данной температуре, которым
должны обладать молекулы веществ для
осуществления химического взаимодействия;
R
- универсальная газовая постоянная; Т
– абсолютная температура.
Функция fi в уравнении (1.2) обычно имеет следующий вид:
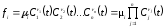 ,
(1.4)
,
(1.4)
где
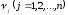 - постоянные положительные величины,
называемые порядками реакции по веществам
- постоянные положительные величины,
называемые порядками реакции по веществам
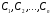 .
.
Стехиометрическое уравнение реакции (1.1) показывает, в каких соотношениях компоненты участвуют в химической реакции. Это уравнение связывает исходные реагенты, конечные продукты и представляет собой уравнение материального баланса реакции в целом или ее отдельных стадий. Если в результате химического взаимодействия а моль вещества А и b моль вещества В образуется с моль вещества С, стехиометрическое уравнение реакции представляется в виде:
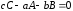 ,
(1.5)
,
(1.5)
где a, b, c – стехиометрические коэффициенты.
Механизм химической реакции раскрывает все элементарные стадии превращения исходных компонентов в конечные продукты через промежуточные вещества. Предположим, что механизм реакции (1.5) включает три стадии:
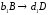 ,
(1.6)
,
(1.6)
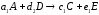 ,
(1.7)
,
(1.7)
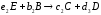 .
(1.8)
.
(1.8)
Здесь А и В – исходные вещества, С- конечный продукт реакции, D – промежуточный продукт. Каждая стадия реакции описывается стехиометрическим уравнением:
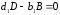 ,
(1.9)
,
(1.9)
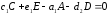 ,
(1.10)
,
(1.10)
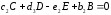 .
(1.11)
.
(1.11)
Реакцию в целом механизма описанного уравнениями (1.6)-(1.8) получают путем суммирования уравнений
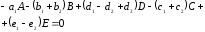 (1.12)
(1.12)
Уравнение (1.12) тождественно уравнению (1.5), если выполняются следующие условия:
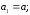
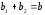 ;
;
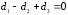 ;
;
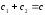 ;
;
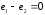 .
.
Скорость химической
реакции
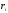 выражается числом
выражается числом
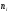 молей компонента, которое образуется
или расходуется в единицу времени в
единице объема V.
Кинетические уравнения реакции имеет
вид:
молей компонента, которое образуется
или расходуется в единицу времени в
единице объема V.
Кинетические уравнения реакции имеет
вид:
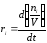 .
(1.13)
.
(1.13)
Отношение числа молей i-го компонента к объему реакционной массы V представляет собой концентрацию этого компонента:
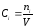 .
(1.14)
.
(1.14)
При постоянном объеме реагентов скорость реакции можно выразить через концентрацию:
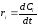 .
(1.15)
.
(1.15)
Скорость реакции типа
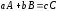 при
постоянной температуре выражается
уравнением:
при
постоянной температуре выражается
уравнением:
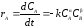 ,
(1.16)
,
(1.16)
где и - определяют порядок реакции, k – константа скорости химических реакций.
Механизм реакции называют истинным, если каждая стадия описывается кинетическим уравнением, составленным в соответствии со стехиометрическим уравнением этой стадии. Приближенный механизм реакции может хорошо аппроксимировать опытные данные по кинетике, но при этом кинетические уравнения скорости не соответствуют стехиометрическим уравнениям. При истинном механизме реакции сумма стехиометрических коэффициентов исходных компонентов равна порядку реакции, а порядок реакции по отдельному компоненту равен стехиометрическому коэффициенту этого компонента.
Например, для реакции
типа
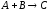 стехиометрическое уравнение записывается
в виде (1.5). Кинетическое уравнение
скорости для продукта реакции выражается
уравнением:
стехиометрическое уравнение записывается
в виде (1.5). Кинетическое уравнение
скорости для продукта реакции выражается
уравнением:
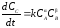 .
(1.17)
.
(1.17)
2. Содержание работы
В данной лабораторной работе необходимо в соответствии с уравнениями химический кинетики построить математические модели реакций нескольких типов.
Задача 1
Построить математическую
модель простой необратимой реакции
первого порядка
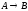 .
Известны начальные концентрации веществ
.
Известны начальные концентрации веществ
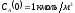 и
и
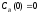 ;
константа скорости химической реакции
при температуре Т1
:
;
константа скорости химической реакции
при температуре Т1
:
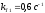 .
Требуется найти кинетические зависимости
компонентов реакции в виде функций
.
Требуется найти кинетические зависимости
компонентов реакции в виде функций
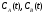 .
.
Решение
Кинетические уравнения имеют вид:
- для компонента А:
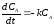 ;
;
- для компонента
В:
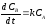 .
.
Уравнения (19) и (20) представляют собой систему линейных дифференциальных уравнений. Максимальные значения концентраций СА и СВ определяются начальной концентрацией реагента А. Рассматриваемая реакция идет до конца, поэтому конечная концентрация продукта В будет численно равна начальной концентрации исходного вещества А:
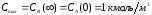 .
.
Полученная система дифференциальных уравнений решается в системе MathCad с помощью встроенной функции rkfixed, реализующей численный метод Рунге-Кутта.
Программа решения в среде MathCad
|
1.
Задаем значение константы скорости
реакции
|
|
2.
Задаем векторную функцию двух аргументов
|
|
3.
Задаем вектор начальных условий
|
|
4.
Задаем число шагов, на которых численно
находится решение
|
|
5. Для решения системы уравнений используем встроенную функцию, реализующую метод Рунге-Кутта с фиксированным шагом
|
|
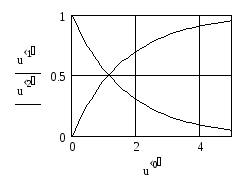
6. Строим графики искомых функций:
|