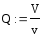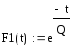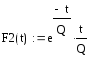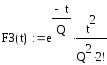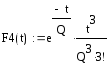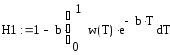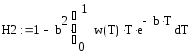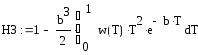ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 94
Скачиваний: 0
Примем
допущения, что гидродинамические условия
протекания процесса выщелачивания
устойчивы и неизменны, тогда
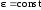 ,
гидродинамические процессы протекают
безынерционно по отношению к химическим,
количество твердого и жидкого веществ
постоянно:
,
гидродинамические процессы протекают
безынерционно по отношению к химическим,
количество твердого и жидкого веществ
постоянно:
 ,
(5.7)
,
(5.7)
 ,
(5.8)
,
(5.8)
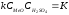 .
(5.9)
.
(5.9)
Тогда материальный баланс по твердому и жидкому веществам опишется уравнением:
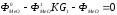 ,
(5.10)
,
(5.10)
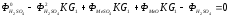 .(5.11)
.(5.11)
В статическом режиме в уравнениях (5.3) и (5.4) производные равны нулю. Тогда, решая совместно уравнения (5.3) и (5.8), (5.4) и (5.9), получим:
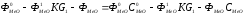 ,
(5.12)
,
(5.12)
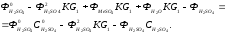 (5.13)
(5.13)
После преобразования получим:
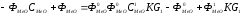 ,
(5.14)
,
(5.14)
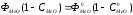 ,
(5.15)
,
(5.15)
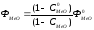 ,
(5.16)
,
(5.16)
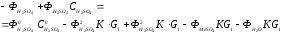 (5.17)
(5.17)
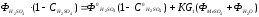 ,
(5.18)
,
(5.18)
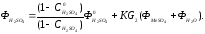 (5.19)
(5.19)
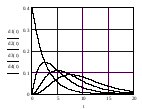
В течение времени похождения пульпы через систему реакторов цинк и сопутствующие ему ценные компоненты должны быть практически полностью переведены в раствор. Вследствие этого извлечение металлов в раствор является основным показателем выщелачивания, который возможно контролировать по степени использования серной кислоты. Для описания процесса выщелачивания используется математическая модель непрерывного гетерогенного процесса. В случае равенства объемов реакторов и с учетом зависимости (5.2) извлечение вещества, достигаемое в каскаде реакторов определяется по уравнению:
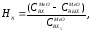 (5.20)
(5.20)
где
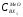 -
концентрация оксидов металлов во входном
потоке;
-
концентрация оксидов металлов во входном
потоке;
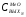 -концентрация
оксидов металлов в выходном потоке N-го
реактора.
-концентрация
оксидов металлов в выходном потоке N-го
реактора.
Извлечение металлов в раствор возможно контролировать по степени использования серной кислоты, количество которой практически определяется автоматическими анализаторами. Поэтому можно записать:
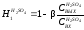 .
(5.21)
.
(5.21)
Система реакторов выщелачивания функционирует в строго установившемся режиме, причем в каждом из аппаратов системы сохраняют свои определенные и постоянные условия. Так как отдельные элементы пульпы пребывают в системе различное время и некоторые из них «проскакивают» систему очень быстро. Превращение вещества никогда не может быть идеально полным. По этой причине нельзя говорить о каком-либо определенном «времени реагирования». Поэтому при оценке работы непрерывно действующей системы реакторов пользовались понятием среднего времени пребывания пульпы в реакторе. В целях уточнения структуры модели приняты следующие допущения: интенсивность перемешивания пульпы в реакторах обеспечивает ее однородность; состав пульпы в реакторе полностью соответствует ее составу на выходе; время усреднения свежего материала, подаваемого в реактор, пренебрежимо мало по сравнению со временем обработки пульпы; объемная скорость потоков пульпы во внутренней и внешней циркуляции каждого реактора постоянны; при определении степени использования серной кислоты применяются следующие понятия.
-
Номинальное время пребывания частиц пульпы в реакторе:
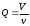 ,
(5.22)
,
(5.22)
где V – объем пульпы в реакторе, v – объемная скорость подачи пульпы.
-
Абсолютное время пребывания отдельных частиц в реакторе или текущее время их реакции оценивают в натуральных единицах.
-
Безразмерное (относительное) время реакции Т:
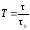 ,
(5.23)
,
(5.23)
где 0 – натуральное время полного или условно полного завершения реакции.
-
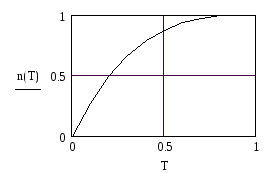
Функция превращения вещества (CT), выражающая долю завершения реакции во времени относительно реагирующего количества:
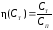 ,
(5.24)
,
(5.24)
где CT, CП – концентрация серной кислоты в получаемом растворе соответственно текущая и предельная.
-
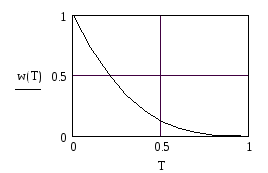
Функция растворения вещества W(CT), выражающая долю недорастворившегося вещества во времени относительно условно полного реагирующего количества:
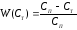 .
(5.25)
.
(5.25)
-
Интегральная функция распределения Ф(Т), выражающая долю потока пульпы или долю частиц вещества, пребывающих в системе реакторов в течение времени меньшего или равного Т. Остальная часть пульпы
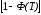 имеет возраст частиц от Т
до
имеет возраст частиц от Т
до
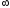 .
.
При
введении в реактор объемом V
с номинальным временем пребывания в
реакторе Q
инертный индикатор в момент времени
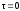 распределившись на пульпе, дает начальную
концентрацию C1,
0.
В дальнейшем концентрация индикатора
снижается и в некоторый момент
равна С1,.
Соответственно доля элементов пульпы,
оставшихся в реакторе и имеющих возраст
,
будет характеризоваться отношением
распределившись на пульпе, дает начальную
концентрацию C1,
0.
В дальнейшем концентрация индикатора
снижается и в некоторый момент
равна С1,.
Соответственно доля элементов пульпы,
оставшихся в реакторе и имеющих возраст
,
будет характеризоваться отношением
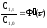 и в момент
устанавливается динамическое равновесие:
и в момент
устанавливается динамическое равновесие:
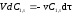 ,
(5.26)
,
(5.26)
которому соответствует выражение
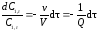 .
(5.27)
.
(5.27)
Последующее
интегрирование с определением постоянной
при
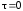 и
и
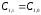 дает:
дает:
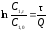 (5.28)
(5.28)
или
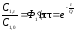 .
(5.29)
.
(5.29)
Для второго реактора каскада уравнение материального баланса имеет вид:
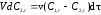 (5.30)
(5.30)
или
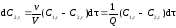 ,
(5.31)
,
(5.31)
где С2, - текущая концентрация индикатора во втором реакторе.
Используя значение С1, , получим:
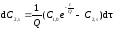 (5.32)
(5.32)
или дифференциальное уравнение первого порядка:
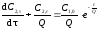 ,
,
решение
которого с определением постоянной при
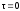 и
и
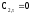 дает:
дает:
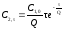 ,
(5.33)
,
(5.33)
и
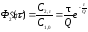 .
(5.34)
.
(5.34)
В общем случае концентрация индикатора в n – ом реакторе каскада:
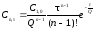 ,
(5.35)
,
(5.35)
а его доля в n – ом реакторе
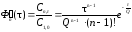 .
(5.36)
.
(5.36)
-
Дифференциальная функция распределения dФ() и dФ(Т) выражает долю потока пульпы или долю частиц вещества, пребывающих в системе реакторов в течении времени от до + d или Т + dT. Остальная часть пульпы представлена дифференциальными элементами, возраст которых меньше и частицами, возраст которых больше ( + d). Общее содержание всех элементов пульпы будет равно единице:
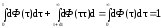 .
(5.37)
.
(5.37)
или
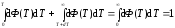 .
(5.38)
.
(5.38)
Для системы реакторов равного объема, установленных последовательно:
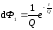 ,
,
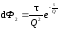 ,
… ,
,
… ,
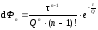 .
(5.39)
.
(5.39)
Общее извлечение или общие потери определяют интегрированием получаемых произведений по всему диапазону возможных значений или Т. Соответственно степень использования серной кислоты, достигаемая в каскаде последовательно установленных реакторов, определяется следующим образом:
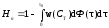 или
или
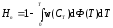 . (5.40)
. (5.40)
-
Содержание работы
В соответствии с вариантом задания с помощью программы, составленной в вычислительной среде MathCAD, провести исследование основных закономерностей процесса выщелачивания.
|
Программа |
|
1. Натуральное время полного или условно полного завершения реакции |
|
t0:=6 |
|
2. Текущее время реакции |
|
|
|
3.Относительное время реакции |
|
|
|
4. Функция превращения вещества |
|
|
|
|
|
|
|
5. Функция растворения вещества |
|
|
|
|
|
6.
Объем реактора
|
|
7.
Объемная скорость подачи раствора
|
|
8. Расчетное время пребывания раствора в каждом аппарате |
|
|
|
9. Коэффициент времени |
|
|
|
10. Число реакторов в каскаде |
|
|
|
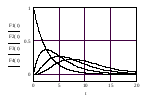
11. Интегральная функция распределения |
|
|
|
|
|
|
|
12. Дифференциальная функция распределения |
|
|
|
|
|
13. Определение степени превращения вещества в реакторах |
|
|
|
|
|
|
|
|