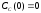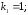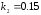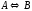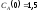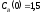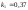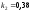ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 95
Скачиваний: 0
Задача 2
Построить модель
двухстадийной последовательной
химической реакции
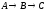 ,
если известны: начальные концентрации
веществ
,
если известны: начальные концентрации
веществ
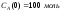 ;
;
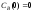 ;
;
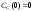 и относительные константы скорости:
и относительные константы скорости:
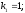
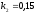 .
.
Решение
Кинетические уравнения имеют вид:
- для компонента
А
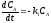 ;
;
-для компонента
В
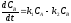 ;
;
- для компонента
С
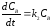 .
.
Программа решения среде MathCad
|
1.
Значения констант скоростей реакций
|
|
|
2.
Вектор-функция
|
|
|
3. Вектор начальных условий |
|
|
4. Число точек для поиска решения |
М:=100 |
|
5. Функция для решения системы |
|
|
|
|
Задача 3
Составить математическую
модель обратимой химической реакции
первого порядка вида
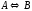 ,
если известны начальные концентрации
,
если известны начальные концентрации
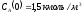 ,
,
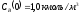 ;
начальные скорости реакции
;
начальные скорости реакции
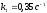 ;
;
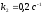 .
.
Решение:
Кинетические уравнения имеют вид:
- для компонента А
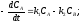
- для компонента В
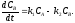
Программа решения среде MathCad
|
1. Значения констант скоростей реакций |
|
|
2. Вектор-функция |
|
|
3. Вектор начальных условий |
М:=100 |
|
4. Число точек для поиска решения
|
|
|
5. Функция для решения системы |
|
|
|
|
3. Порядок выполнения работы
1. В соответствии с
вариантом задания построить кинетическую
модель необратимой реакции первого
порядка
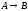 ,
решить математическую модель в системе
MathCAD
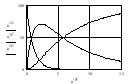
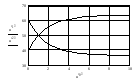
и построить графики кинетических кривых,
полученных на модели.
,
решить математическую модель в системе
MathCAD
и построить графики кинетических кривых,
полученных на модели.
2. Построить модель
двухстадийной последовательной
химической реакции
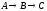 ,
решить модель в системе MathCAD
и построить графики кинетических кривых,
полученных на модели.
,
решить модель в системе MathCAD
и построить графики кинетических кривых,
полученных на модели.
3. Составить модель
обратимой химической реакции первого
порядка вида
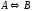 ,
решить математическую модель в системе
MathCAD
и построить графики кинетических кривых,
полученных на модели.
,
решить математическую модель в системе
MathCAD
и построить графики кинетических кривых,
полученных на модели.
4. Исходными данными являются значения концентраций веществ, участвующих в реакциях, и констант скоростей реакций, численные значения которых представлены ниже.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Содержание отчета
4.1. Тема и цель работы, номер варианта
4.2. Постановка задачи
4.3. Математические модели реакций и графики кинетических зависимостей
4.4. Выводы
5. Контрольные вопросы
5.1. Какая химическая реакция называется простой?
5.2. Что представляет собой константа скорости реакции, от каких параметров она зависит?
5.3. Что показывают стехиометрические коэффициенты?
5.4. Какой механизм реакции называется истинным?
Лабораторная работа №3
Применение численных методов для решения простейших задач теплообмена
Цель работы: изучить метод Ньютона для решения нелинейных уравнений и использовать его при решении задачи радиационного теплообмена.
-
Теоретические положения
1.1. Постановка задачи
Пусть
требуется рассчитать температуру
нагревателя
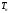 электрической печи сопротивления.
электрической печи сопротивления.
Считаем заданными:
-
температуру поверхности нагреваемого металла
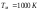 ;
; -
степень черноты поверхности нагреваемого металла
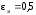
-
полезную удельную мощность нагревателя
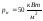 ;
; -
зависимость степени черноты нагревателя от температуры
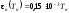 (в интервале 1000-2000 К).
(в интервале 1000-2000 К).
Для решения данной задачи запишем уравнение теплового баланса нагревателя:
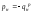 ,
(4.1)
,
(4.1)
где
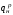 -
плотность потока результирующего
излучения на его поверхности.
-
плотность потока результирующего
излучения на его поверхности.
Выразим
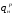 через
неизвестную температуру
через
неизвестную температуру
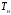 ,
рассматривая поверхности нагревателя
и металла как бесконечные параллельные
плоскости:
,
рассматривая поверхности нагревателя
и металла как бесконечные параллельные
плоскости:
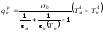 ,
(4.2)
,
(4.2)
где
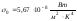 - постоянная Стефана - Больцмана.
- постоянная Стефана - Больцмана.
Подставив выражение (3.2) в уравнение теплового баланса (3.1), получим:
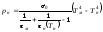 .
(4.3)
.
(4.3)
Зависимость
(3.3) представляет собой нелинейное
уравнение относительно искомой
температуры
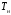 .
Для решения поставленной задачи
рассмотрим применение метода Ньютона
(метода касательных).
.
Для решения поставленной задачи
рассмотрим применение метода Ньютона
(метода касательных).
-
Метод Ньютона (метод касательных)
Данный метод предназначен
для решения нелинейных уравнений вида:
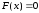 ,
(4.4)
,
(4.4)
где функция
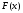 определена и непрерывна на конечном
или бесконечном интервале
определена и непрерывна на конечном
или бесконечном интервале
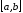 .
Всякое число
.
Всякое число
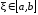 ,
обращающее функцию
,
обращающее функцию
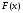 в нуль, называется корнем уравнения
в нуль, называется корнем уравнения
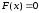 .
Пусть корень уравнения
.
Пусть корень уравнения 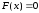 отделен на отрезке [a,
b],
причем
отделен на отрезке [a,
b],
причем
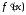 и
и
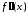 непрерывны
и сохраняют определенные знаки при
непрерывны
и сохраняют определенные знаки при
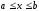 .
Если на некотором произвольном шаге n
найдено приближенное значение корня
.
Если на некотором произвольном шаге n
найдено приближенное значение корня
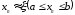 ,
то можно уточнить это значение по методу
Ньютона. Положим
,
то можно уточнить это значение по методу
Ньютона. Положим
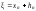 , (4.5)
, (4.5)
где 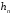 - малая величина.
- малая величина.
Применяя формулу Тейлора, получим:
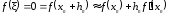 .
.
Следовательно,
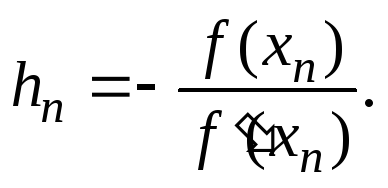
Внеся эту поправку в формулу (3.1), найдем следующее (по порядку) приближение корня:
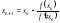 ,
,
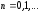 (4.6)
(4.6)
Геометрически метод
Ньютона эквивалентен замене дуги кривой
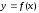 касательной,
проведенной в некоторой точке кривой
(рис. ). Положим для определенности, что
касательной,
проведенной в некоторой точке кривой
(рис. ). Положим для определенности, что
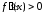 при
при
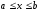 и
и
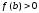 .
Выберем,
.
Выберем,
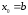 ,
для которого
,
для которого
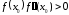 .
Проведем касательную к кривой
.
Проведем касательную к кривой
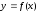 в
точке B0
с координатами
в
точке B0
с координатами
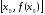 .
В качестве первого приближения
.
В качестве первого приближения
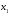 корня
возьмем абсциссу точки пересечения
касательной с осью Ox.
корня
возьмем абсциссу точки пересечения
касательной с осью Ox.
Рисунок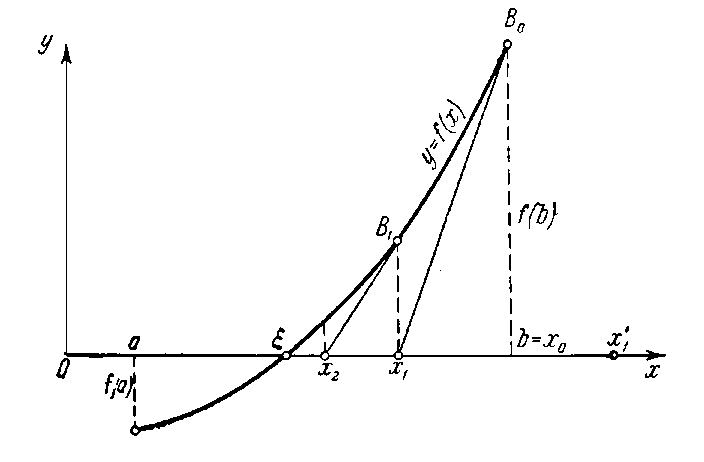
Рис. Геометрическая интерпретация метода Ньютона
Через точку
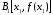 снова проведем касательную, абсцисса
точки пересечения которой даст второе
приближение
снова проведем касательную, абсцисса
точки пересечения которой даст второе
приближение
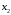 корня и т.д. Формулу для уточнения корня
можно получить из треугольника
корня и т.д. Формулу для уточнения корня
можно получить из треугольника
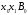 ,
образованного касательной, проведенной
в точке B0,
осью абсцисс и перпендикуляром,
восстановленным из точки
,
образованного касательной, проведенной
в точке B0,
осью абсцисс и перпендикуляром,
восстановленным из точки
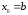 .
Тогда
.
Тогда
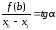 .
Так как угол
образован касательной и осью абсцисс,
его тангенс численно равен величине
производной, вычисленной в точке,
соответствующей абсциссе точки касания,
т.е.
.
Так как угол
образован касательной и осью абсцисс,
его тангенс численно равен величине
производной, вычисленной в точке,
соответствующей абсциссе точки касания,
т.е.
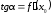 и
и
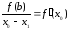 .
Тогда справедливо, что
.
Тогда справедливо, что
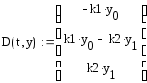
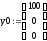
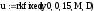
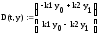
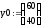
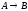
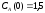
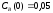
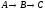
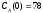 ;
;
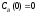 ;
;
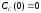
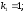
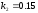
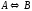
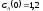
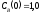
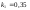
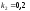
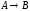
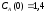
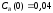
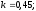
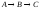
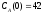 ;
;
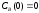 ;
;
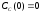
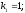
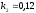
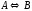
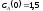

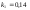
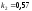
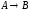
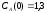
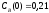
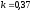
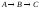
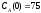 ;
;
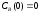 ;
;
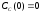
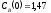
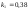
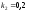
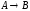
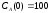
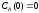
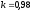
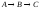
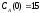 ;
;
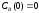 ;
;
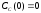
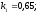
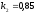
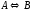
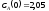
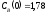
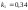
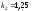
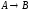
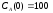
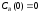
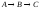
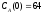 ;
;
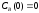 ;
;
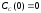
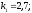
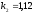
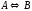
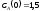
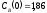
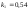
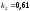
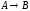
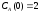
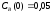
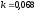
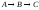
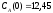 ;
;
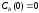 ;
;
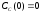
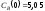
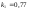
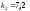
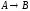
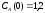

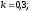
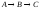
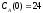 ;
;
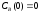 ;
;
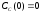
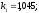
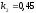
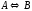
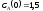
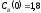
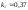
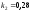
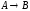
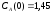
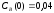
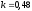
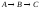
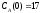 ;
;
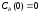 ;
;
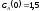
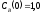
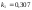
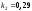
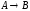
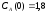
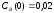
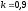
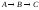
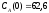 ;
;
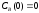 ;
;
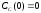
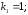
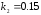

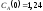
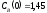
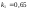
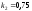
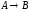
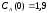
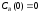
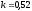
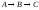
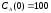 ;
;
 ;
;