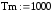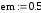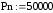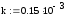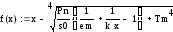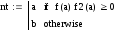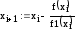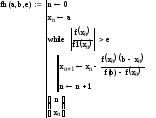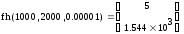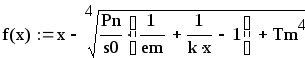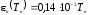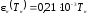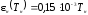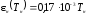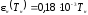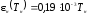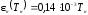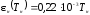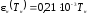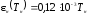ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 101
Скачиваний: 0
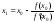 (4.7)
(4.7)
или для любого шага n
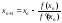 .
(4.8)
.
(4.8)
В качестве начальной
точки
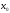 можно
принять либо один из концов отрезка [a,
b],
либо точку внутри этого интервала. В
первом случае рекомендуется выбирать
ту границу, где выполняется условие
можно
принять либо один из концов отрезка [a,
b],
либо точку внутри этого интервала. В
первом случае рекомендуется выбирать
ту границу, где выполняется условие
![]()
т.е. функция и ее вторая
производная в точке
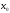 должны
быть одного знака.
должны
быть одного знака.
При использовании метода Ньютона исходное уравнение необходимо привести к виду:
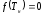 .
(4.9)
.
(4.9)
Тогда в левой части уравнения (4.3) окажется функция:
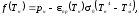 (4.10)
(4.10)
где
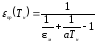 - приведенная степень черноты
рассматриваемой системы.
- приведенная степень черноты
рассматриваемой системы.
Значение
уравнения (4.10) при текущем значении
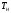 называют
невязкой уравнения (4.9). На каждом шаге
итераций последующему приближению
искомой величины соответствует точка
пересечения с остью абсцисс касательной
к кривой
называют
невязкой уравнения (4.9). На каждом шаге
итераций последующему приближению
искомой величины соответствует точка
пересечения с остью абсцисс касательной
к кривой
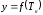 в точке предыдущего приближения. С
учетом того, что тангенс угла наклона
касательной численно равен производной
от невязки исследуемой функции:
в точке предыдущего приближения. С
учетом того, что тангенс угла наклона
касательной численно равен производной
от невязки исследуемой функции:
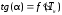 ,
получим следующее выражение для
,
получим следующее выражение для
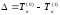 :
:
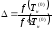 ,
(4.11)
,
(4.11)
т. е. последующее приближение может быть найдено по формуле:
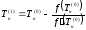 .
(4.12)
.
(4.12)
В общем случае итерационная формула для метода Ньютона имеет вид:
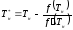 . (4.13)
. (4.13)
В
процессе расчета по этой формуле значения
искомой температуры нагревателя быстро
приближаются к решению исходного
уравнения, при этом значения невязок
стремятся к нулю. Рассмотрим особенности
применения метода Ньютона для решения
рассматриваемой задачи теплообмена.
Отметим, что рассчитывать производную
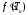 можно достаточно приближено, т. к. ее
величина определяет лишь значение
очередного приближения, не влияя на
окончательный результат расчета.
Пренебрегая зависимостью
можно достаточно приближено, т. к. ее
величина определяет лишь значение
очередного приближения, не влияя на
окончательный результат расчета.
Пренебрегая зависимостью
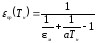 при дифференцировании невязки, получим
выражение для приближенного значения
производной:
при дифференцировании невязки, получим
выражение для приближенного значения
производной:
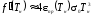 (4.14)
(4.14)
и итерационная формула примет вид:
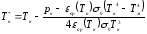 .
(4.15)
.
(4.15)
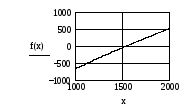
Решение поставленной задачи реализовано в вычислительной среде MathCAD. Расчет по формуле (3.15) приводит к значению искомой величины: 1544,3. Программа, реализующая алгоритм метода Ньютона в системе MathCAD, представлена ниже.
|
Программа |
|
1. Задаем исходные данные: |
|
Температура
поверхности металла:
|
|
Степень
черноты поверхности
нагреваемого металла:
|
|
Полезная
удельная мощность нагревателя:
|
|
Зависимость
степени черноты нагревателя от
температуры
|
|
Отделяем корни уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Вычисляем значения итерационной последовательности с использованием рекуррентной формулы метода касательных:
|
|
|
|
|
|
|
|
4. Создаем функцию, реализующую метод касательных |
|
|
|
|
|
5. Проверяем полученные результаты |
|
|
4. Задание для выполнения
|
|
Вар. №1 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1100 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,5 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
55 |
|
4. |
Зависимость степени черноты нагревателя от температуры, |
|
|
|
Вар. №2 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1200 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,55 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
60 |
|
4. |
Зависимость степени черноты нагревателя от температуры, |
|
|
|
Вар. №3 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1300 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,6 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
65 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №4 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1400 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,65 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
70 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №5 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1500 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,7 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
75 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №6 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1600 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,75 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
80 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №7 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1700 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,8 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
85 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №8 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
1800 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,85 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
90 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №9 |
|
|
|
Температура поверхности нагреваемого металла (Тм), К |
1900 |
|
|
Степень черноты поверхности нагреваемого металла, em |
0,9 |
|
|
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
95 |
|
|
Зависимость степени черноты нагревателя от температуры, en |
|
|
|
Вар. №10 |
|
|
1. |
Температура поверхности нагреваемого металла (Тм), К |
2000 |
|
2. |
Степень черноты поверхности нагреваемого металла, em |
0,95 |
|
3. |
Полезная удельная мощность нагревателя, кВт/ м2 (рn) |
100 |
|
4. |
Зависимость степени черноты нагревателя от температуры, en |
|
5. Контрольные вопросы
-
Какой физический смысл имеет уравнение, используемое для получения решения?
-
Что является причиной нелинейности уравнения?
-
В чем состоит идея метода Ньютона?
-
Какие существуют еще методы для численного решения нелинейных уравнений?
Лабораторная работа №4
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ВЫЩЕЛАЧИВАНИЯ
ЦИНКОВЫХ ОГАРКОВ
Цель работы: построить математическую модель каскада реакторов процесса выщелачивания цинковых огарков и провести с ее помощью исследование процесса.
1. Теоретические положения
Основная цель выщелачивания цинкового огарка – возможно более полное извлечение в раствор цинка и сопутствующих ему ценных компонентов при минимальном загрязнении примесями, вредными для последующих операций. Взаимодействие компонентов огарка и отработанного электролита осуществляется по реакции:
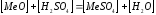 (5.1)
(5.1)
Реакции растворения необратимы, так как не зависят от концентрации продуктов реакции. Твердые и газообразные продукты реакции и исходные вещества могут влиять только экранированием растворяющейся фазы. Температура и гидродинамические параметры выщелачивания определяют скорость растворения кинетическими и диффузионными факторами. Скорость выщелачивания может быть описана уравнениями химической кинетики:
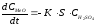 ,
(5.2)
,
(5.2)
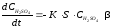 ,
(5.3)
,
(5.3)
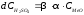 ,
(5.4)
,
(5.4)
где
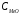 - концентрация оксидов металлов;
- концентрация оксидов металлов;
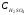 -
концентрация серной кислоты; S
– поверхность твердой фазы;
- стехиометрический коэффициент,
определяющий расход реагента (в молях)
на один моль сырья.
-
концентрация серной кислоты; S
– поверхность твердой фазы;
- стехиометрический коэффициент,
определяющий расход реагента (в молях)
на один моль сырья.
Для гетерогенного процесса, описываемого псевдогомогенной моделью, уравнение материального баланса может быть представлено в виде:
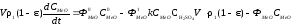 ,
(5.5)
,
(5.5)
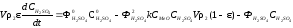 ,
(5.6)
,
(5.6)
где
V
– объем реакционной смеси; 1,
2
– плотность твердой фазы;
- порозность реакционой смеси;
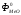 ,
,
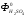 -
входные потоки твердого и жидкого
вещества;
-
входные потоки твердого и жидкого
вещества;
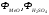 - выходные потоки твердого и жидкого
веществ;
- выходные потоки твердого и жидкого
веществ;
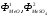 -
потоки компонентов реакции, подаваемых
в стехиометрических необходимых
количествах;
-
потоки компонентов реакции, подаваемых
в стехиометрических необходимых
количествах;
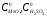 -
концентрации веществ во входном потоке;
k
–
константа скорости реакции.
-
концентрации веществ во входном потоке;
k
–
константа скорости реакции.