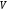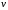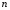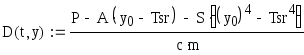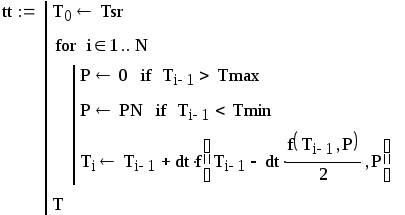Файл: Лабораторные.docx

3. Задание для выполнения

Вар.
1	6,5	0,5	200	80	5
2	6	0,550,5	150	70	4
3	5,5	0,49	140	75	6
4	5	0,48	160	80	5
5	4,5	0,47	170	85	4
6	4,7	0,46	180	90	6
7	4,6	0,45	190	80	3
8	5,1	0,44	200	85	5
9	5,2	0,43	190	95	4
10	5,4	0,44	180	90	3

---

4. Содержание отчета

1. Тема работы.

2. Постановка задачи.

3. Расчет основных показателей процесса с помощью математической модели.

4. Графики основных показателей процесса выщелачивания: функция превращения вещества, функция растворения вещества, дифференциальная функция распределения, интегральная функция распределения, зависимость извлечения ценного компонента по каскаду реакторов.

5. Выводы

5. Контрольные вопросы

5.1. К какому типу относится математическая модель процесса выщелачивания?

5.2. Какие допущения приняты при построении модели?

5.3. В чем состоит смысл функций растворения и превращения?

5.4. Что показывают интегральная и дифференциальная функции распределения?

Лабораторная работа №5

МОДЕЛИРОВАНИЕ РАБОТЫ ЭЛЕКТРИЧЕСКОГО

НАГРЕВАТЕЛЯ И ИССЛЕДОВАНИЕ СИСТЕМЫ

ДВУХПОЗИЦИОННОГО РЕГУЛИРОВАНИЯ

ТЕМПЕРАТРУРЫ

Цель работы: получать практические навыки моделирования работы электрического нагревателя и исследования на его модели системы двухпозиционного регулирования температуры.

6.1. Постановка задачи

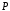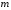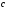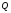Известна мощность нагревателя , его масса и удельная теплоемкость . Потери тепла происходят за счет теплопроводности среды и конвекции по закону:

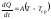, (6.1)

где T – температура нагревателя, 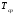- температура окружающей среды, А – коэффициент

а также за счет излучения в соответствии с законом Стефана-Больцмана:

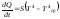, (6.2)

где 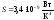- приведенный коэффициент теплообмена излучением.

Нагреватель снабжен терморегулятором, который включает его, если температура 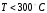и выключает в случае превышения температуры .

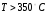Математическую модель объекта составим на основании уравнений теплового баланса. Часть подводимой к нагревателю энергии 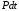расходуется на его нагрев:

---

, (6.3)

а на потери в окружающую среду уходит энергия:

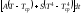. (6.4)

Если не учитывать действия терморегулятора, дифференциальное уравнение, описывающее нарастание температуры во времени, имеет вид:

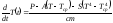. (6.5)

6.2. Содержание работы

В данной лабораторной работе необходимо выполнить:

6.2.1. моделирование работы нагревателя без учета системы регулирования,

6.2.2. моделирование системы двухпозиционного регулирования температуры нагревателя.

6.3. Порядок выполнения работы:

6.3.1. Получить вариант задания у преподавателя.

6.3.2. В соответствии с исходными данными решить дифференциальное уравнение математической модели нагревателя. Для решения можно использовать встроенные функции вычислительной среды MathCAD. В примере 1 решения, приведенном ниже, используется функция 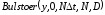. Данная функция возвращает матрицу решений обыкновенных дифференциальных уравнений методом Булирша-Штера с постоянным шагом с заданными начальными условиями в векторе 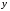на интервале от 0 до 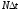в 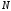точках. Зададим начальное условие 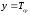и выразим первую производную:

.

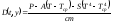Пример 1.

1. Исходные данные

Мощность нагревателя

Масса нагревателя

Удельная теплоемкость нагревателя

Число точек

Расстояние между точками

Температура окружающей среды

Коэффициент

Приведенный коэффициент теплообмена излучением

2. Задаем вектор-функцию

3. Задаем начальное условие

4. Вызываем встроенную функцию для решения уравнения

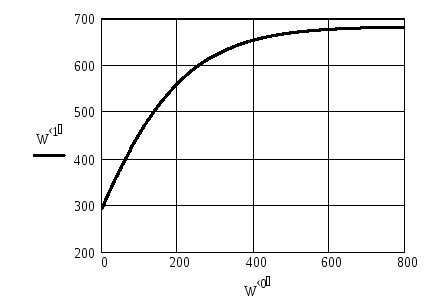
5. Визуализируем решение

---

Рис. 6.1. Графическое решение дифференциального уравнения

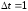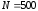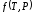6.3.3. В соответствии с исходными данными провести моделирование двухпозиционной системы регулирования температуры нагревателя. Для моделирования работы системы двухпозиционного регулирования температуры нагревателя уравнение (6.5) решим модифицированным методом Эйлера. Зададим шаг приращения во времени . Возьмем число шагов . Тогда функция определит производную от температуры по времени:

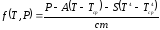. (6.6)

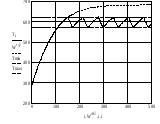
Для расчета температуры составлена программа (см. пример 2), реализующая алгоритм ее вычисления и учитывающая действие терморегулятора.

Пример 2.

Рис. 6.2. Результат моделирования двухпозиционной системы регулирования

6.4. Исходные данные и варианты

Варианты заданий для выполнения приведены в табл. 6.1.

Таблица 6.1.

Вар.	PN	m	Tsr	A	Tmin	Tmax	dt
1	1000	1,0	290	2,0	500	600	1,0
2	1050	1,1	291	2,1	510	620	1,1
3	1100	1,2	292	2,2	520	640	1,2
4	1150	1,3	293	2,0	530	660	1,3
				Продолжение таблицы 6.1.
5	1200	1,4	294	2,1	540	680	1,4
6	1250	1,5	290	2,2	550	700	1,5
7	1300	1,6	291	2,0	560	600	1,56
8	1350	1,7	292	2,1	570	620	1,7
9	1400	1,8	293	2,2	580	640	1,8
10	1450	1,9	294	2,0	590	660	1,9
11	1500	2,0	290	2,1	600	680	2,0
12	1550	2,1	291	2,2	610	700	2,1
13	1600	2,3	292	2,0	620	615	2,2
14	1650	2,4	293	2,1	630	635	2,3
15	1700	2,5	294	2,2	640	645	2,4

---

6.5. Требования к отчету.

Отчет по лабораторной работе должен содержать:

6.5.1. Постановку задачи (теоретические сведения),

6.5.2. Номер варианта и исходные данные для расчетов,

6.5.3. Решение дифференциального уравнения, описывающее изменение температуры нагревателя без регулирования,

6.5.4. Результаты моделирования двухпозиционной системы регулирования температуры нагревателя.

6.5.5. Выводы

6.6. Контрольные вопросы

6.6.1. Какие физические явления обусловливают потери тепла нагревателя? В чем состоит их сущность?

6.6.2. Какое уравнение лежит в основе математической модели нагревателя?

6.6.3. По какому принципу осуществляется решение дифференциальных уравнений в системе MathCad?

6.6.4. В чем заключается метод Эйлера для решения дифференциальных уравнений?

6.6.6. В чем заключается принцип двухпозиционного регулирования?

Лабораторная работа №6

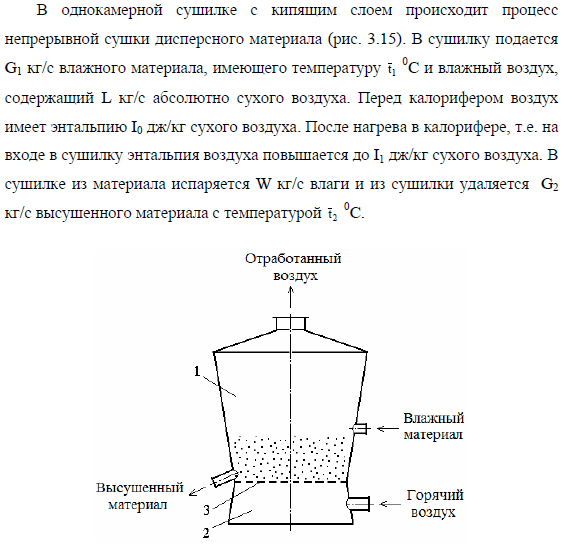
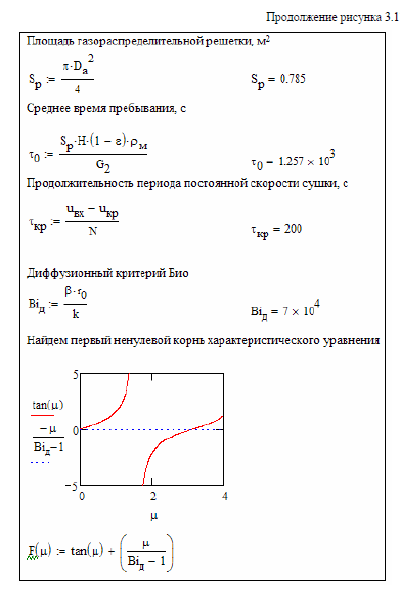
Моделирование сушилки с кипящим слоем

Цель: разработать исследовать математическую модель сушилки с кипящим слоем

---