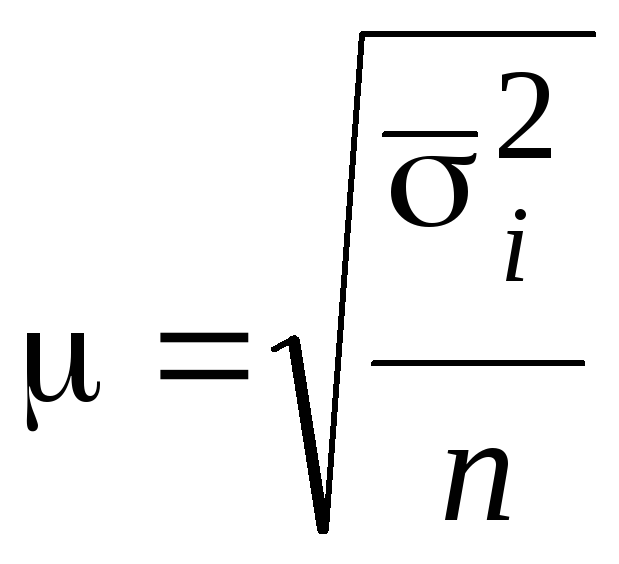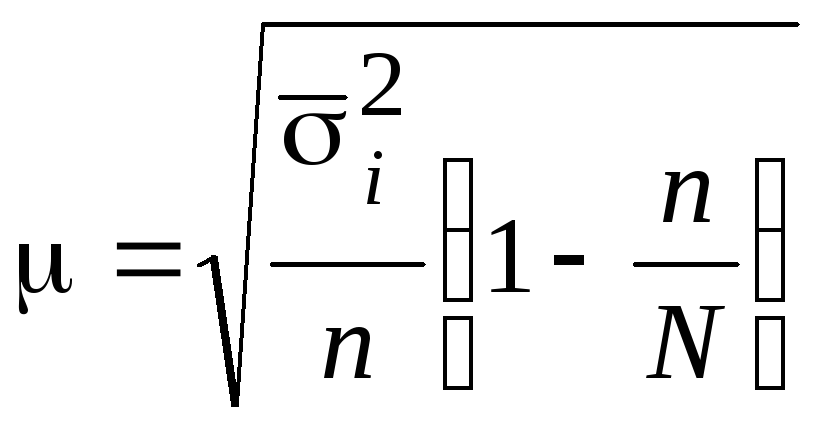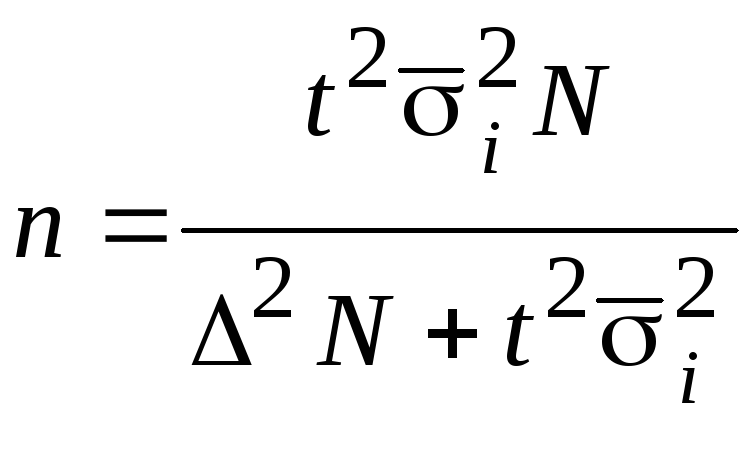ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 138
Скачиваний: 0
СОДЕРЖАНИЕ
Лекции по общей теории статистики
Тема 1. Введение. Предмет и метод статистической науки
1.1. История развития статистической науки
1.2. Предмет и метод статистической науки
1.3. Организация и функции статистических служб
Тема 2. Статистическое наблюдение
2.1. Статистическое наблюдение.
2.2. Сводка и группировка статистических данных
2.3. Принципы построения статистических группировок
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
3.3. Средние структурные величины
4.1. Понятие вариационных рядов.
Графическое отображение вариационных рядов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
5.2. Закон больших чисел и предельные теоремы
5.3 Формы организации выборочного наблюдения
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Оценка линейного коэффициента корреляции
7.2 Методы анализа тенденций рядов динамики
7.3. Статистические методы прогнозирования экономических показателей
8.2. Общие индексы количественных показателей
8.3. Общие индексы качественных показателей
8.4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Существуют следующие виды дисперсий:
Общая дисперсия совокупности
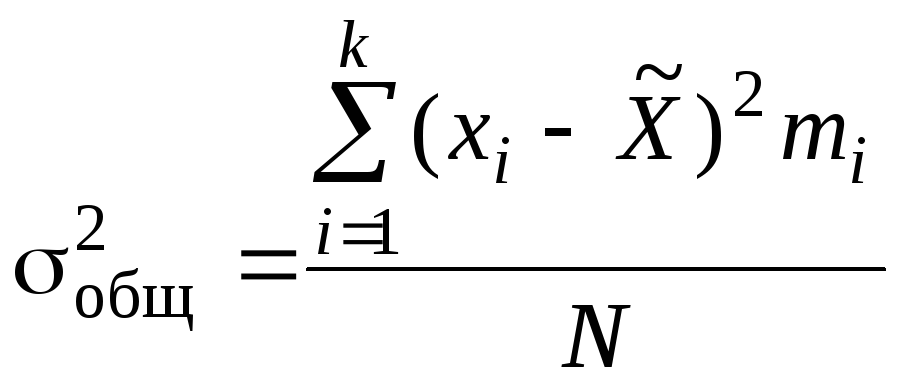 . (4.15)
. (4.15)
Общая дисперсия отражает вариацию признака за счет всех факторов, действующих в данной совокупности.
Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как средний квадрат отклонений групповой средней от общей средней:
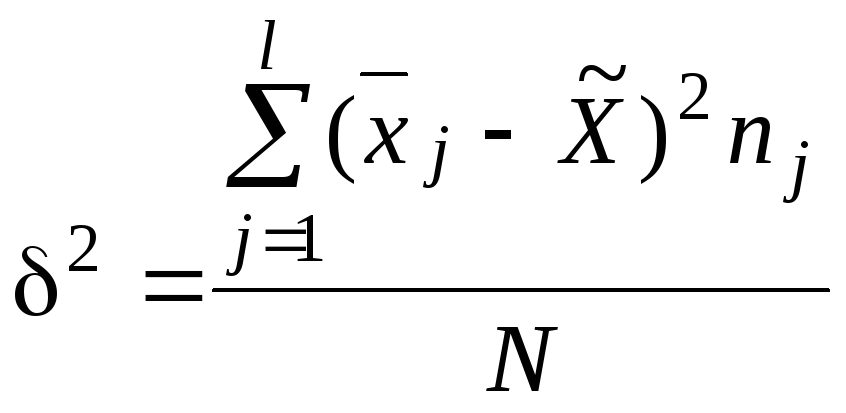 . (4.18)
. (4.18)
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, т.е. вариацию между группами за счет признака-фактора, положенного в основу группировки.
Вариацию
внутри каждой группы изучаемой
совокупности отражает внутригрупповая
дисперсия,
которая
исчисляется как средний квадрат
отклонений значений признака х
от частной средней
![]() :
:
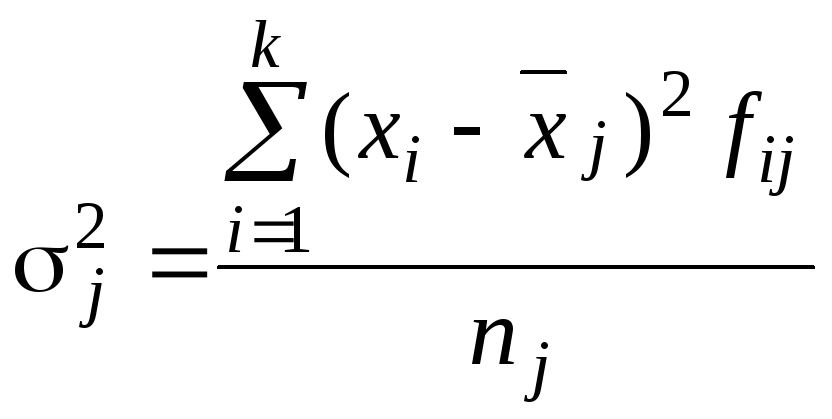 или
или
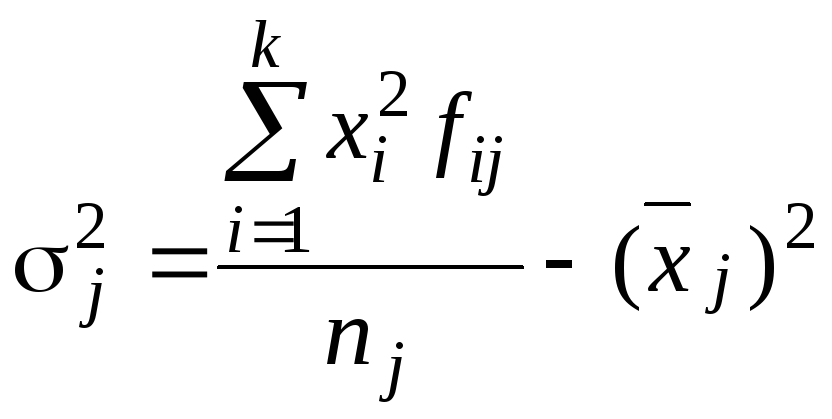 . (4.19)
. (4.19)
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки.
Между представленными видами дисперсий существует определенное соотношение, которое известно как правило сложения дисперсий:
![]() . (4.20)
. (4.20)
Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсий. Это соотношение называется эмпирическим коэффициентом детерминации (η2) и показывает долю вариации результативного признака под влиянием факторного.
![]() . (4.21)
. (4.21)
Эмпирическое корреляционное отношение (η) показывает тесноту связи между исследуемым явлением и группировочным признаком.
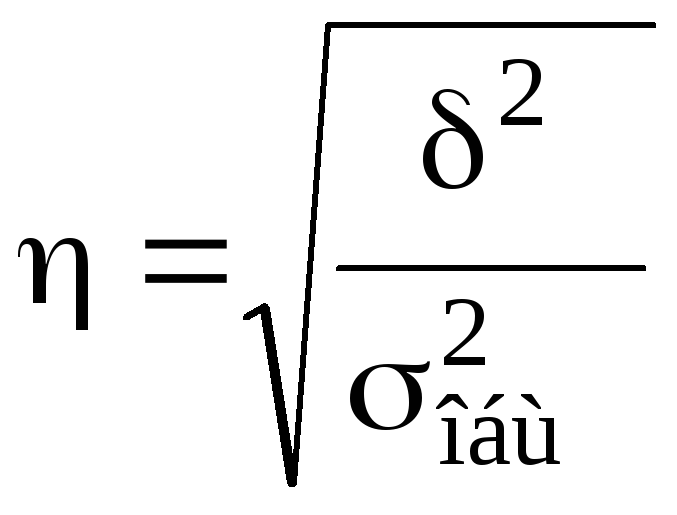 . (4.22)
. (4.22)
η2
и η
![]() [0, 1]. (4.23)
[0, 1]. (4.23)
Если связь отсутствует, то h = 0. В этом случае межгрупповая дисперсия равна нулю (δ2=0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х.
Если
связь функциональная, то h
= 1. В этом случае дисперсия групповых
средних равна общей дисперсии (![]() ).
Это означает, что группировочный признак
полностью определяет характер изменения
изучаемого признака.
).
Это означает, что группировочный признак
полностью определяет характер изменения
изучаемого признака.
Чем больше значение корреляционного отношения приближается к единице, тем полнее (сильнее) корреляционная связь между признаками (таблица 4.3).
Таблица 4.3 - Оценка связи между признаками (шкала Чэддока)
|
Значение
|
Характер связи |
Значение
|
Характер связи |
|
η = 0 |
Отсутствует |
0,5 ≤ η < 0,7 |
Заметная |
|
0 < η < 0,2 |
Очень слабая |
0,7 ≤ η < 0,9 |
Сильная |
|
0,2 ≤ η < 0,3 |
Слабая |
0,9 ≤ η < 1 |
Весьма сильная |
|
0,3 ≤ η < 0,5 |
Умеренная |
η = 1 |
Функциональная |
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
Наиболее широко распространенным видом несплошного наблюдения является выборочное наблюдение, при котором обследуются не все единицы изучаемой совокупности, а лишь определенным образом отобранная их часть.
Вся подлежащая изучению совокупность объектов (наблюдений) называется генеральной совокупностью. Выборочной совокупностью или выборкой называется часть генеральной совокупности, отобранная для изучения свойств обеспечивающая репрезентативность. Отбор из генеральной совокупности проводится таким образом, чтобы на основе выборки можно было получить достаточно точное представление об основных параметрах совокупности в целом. Главное требование, которому должна отвечать выборочная совокупность, — это требование ее репрезентативности, т.е. представительности.
Ошибкой статистического наблюдения считается величина отклонения между расчетным и фактическим значениями признаков изучаемых объектов.
Основные этапы выборочного наблюдения;
1) определение цели, задач и составление программы наблюдения;
2) формирование выборки;
3) сбор данных на основе разработанной программы;
4) анализ полученных результатов и расчет основных характеристик выборочной совокупности;
5) расчет ошибки выборки и распространение ее результатов на генеральную совокупность.
Различают виды выборки:
случайная (собственно-случайная);
механическая (например, каждый 10, 20 и т.д.);
типическая (стратифицированная), когда генеральная совокупность разбита на группы и в каждой группе обследуются по нескольку объектов));
серийная (гнездовая), когда случайным образом отбираются целые серии.
Наиболее простой способ формирования выборочной совокупности – собственно случайный отбор. Теоретические основы выборочного метода, первоначально разработанные применительно к собственно случайному отбору, используют и для определения ошибок выборки при других способах наблюдения.
Собственно случайный отбор может быть повторным и бесповторным. При повторном отборе каждая единица, отобранная в случайном порядке из генеральной совокупности, после проведения наблюдения возвращается в эту совокупность и может быть вновь подвергнута обследованию. На практике такой способ отбора встречается редко. Гораздо более распространен собственно случайный бесповторный отбор, при котором обследованные единицы в генеральную совокупность не возвращаются и не могут быть обследованы повторно. При повторном отборе вероятность попадания в выборку для каждой единицы генеральной совокупности остается неизменной. При бесповторном отборе она меняется, но для всех единиц, оставшихся в генеральной совокупности после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова.
5.2. Закон больших чисел и предельные теоремы
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Или иначе: При большом числе случайных величин их средней результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Среднее квадратическое отклонение ошибок выборки
![]() , (5.7)
, (5.7)
![]() . (5.8).
. (5.8).
Зная
выборочную среднюю
![]() и предельную ошибку выборки
и предельную ошибку выборки![]() можно определить границы, в которых
размещена генеральная средняя
можно определить границы, в которых
размещена генеральная средняя![]() .
.
Предельная
ошибка выборки
![]() может быть определена по формуле
может быть определена по формуле
![]() .
.
Величина
дисперсии генеральной совокупности
![]() принципиально не известна и можно
говорить лишь о ее оценке по результатам
одной выборки.
принципиально не известна и можно
говорить лишь о ее оценке по результатам
одной выборки.
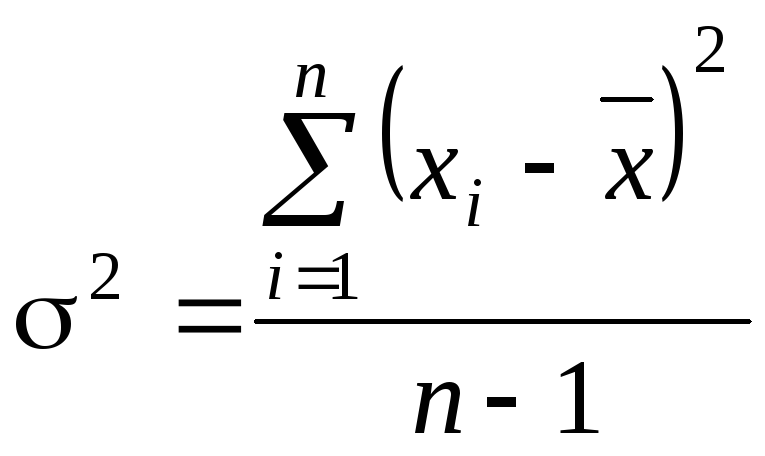 –для простой
случайной выборки.
–для простой
случайной выборки.
Выборочное наблюдение
|
Наименование показателя |
Вид выборки |
|
|
повторная |
бесповторная |
|
|
Случайная выборка Средняя ошибка |
|
|
|
Средняя ошибка доли признака |
|
|
|
Объем выборки |
|
|
|
Типическая выборка
Средняя ошибка |
|
|
|
Объем выборки |
|
|
|
Серийная выборка
Средняя ошибка |
|
|
|
Объем выборки |
|
|
Величина
ошибки зависит от колеблемости признака
в генеральной совокупности и от объема
выборки. Т.е. чем больше вариация тем
больше ошибка, чем больше выборка, тем
меньше ошибка. Величину
![]() называют предельной ошибкой выборки.
Следовательно, предельная ошибка выборки
называют предельной ошибкой выборки.
Следовательно, предельная ошибка выборки![]() ,
т.е. предельная ошибка равнаt-кратному
числу средних ошибок выборки.
,
т.е. предельная ошибка равнаt-кратному
числу средних ошибок выборки.
t– коэффициент доверия
n – объем выборки;
N – объем генеральной совокупности;
s - число отобранных серий;
S – общее число серий;
![]() -
средняя из групповых дисперсий;
-
средняя из групповых дисперсий;
![]() -
межгрупповая дисперсия.
-
межгрупповая дисперсия.
5.3 Формы организации выборочного наблюдения
Типическая (стратифицированная) выборка: общий список разбивается на отдельные списки (однородной группы). Общий объем выборки n разбивается пропорционально между списками:
1-й вариант
![]() , (5.24)
, (5.24)
где n – объем выборки
N – объем генеральной совокупности
ni – число наблюдений из i-ой типической группы
Ni – объем i-ой типической группы в генеральной совокупности.
2-й вариант – равномерный (из каждой группы поровну)
![]() , (5.25)
, (5.25)
где k – число групп.
3-й вариант – оптимальный (для групп с большей вариацией признака объем наблюдений увеличивается)
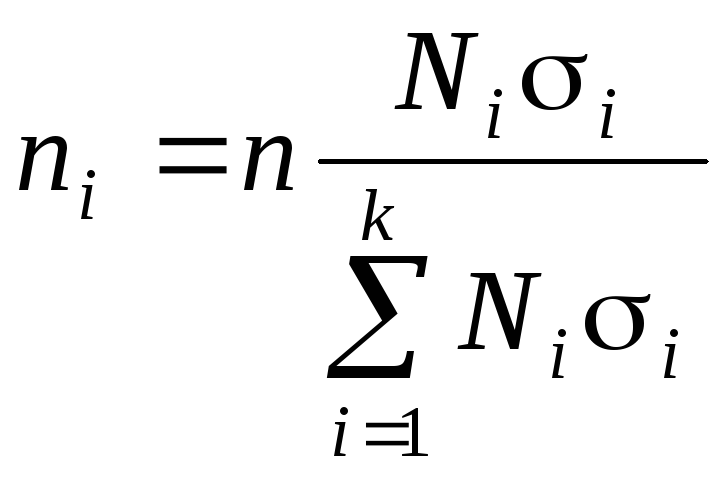 . (5.26)
. (5.26)
Серийная
(гнездовая) выборка
– в случайном порядке отбираются серии
сплошного контроля. Тогда
![]() в сериях определяется без случайной
ошибки. При равновеликих сериях
стандартная ошибка выборки определяется
в сериях определяется без случайной
ошибки. При равновеликих сериях
стандартная ошибка выборки определяется
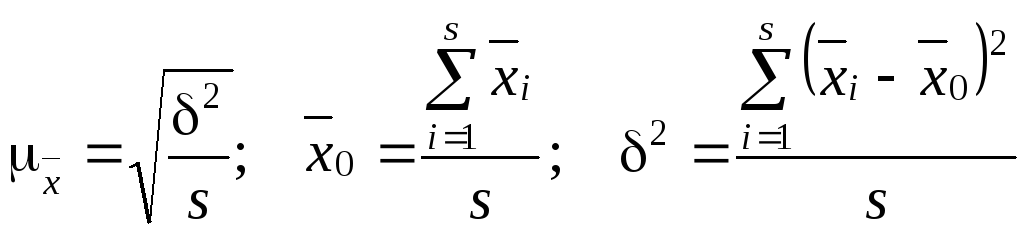 ,(5.27)
,(5.27)
где s – число серий;
δ – межгрупповая дисперсия.
При бесповторном отборе
![]() , (5.28)
, (5.28)
где S – общее число серий в генеральной совокупности.
Механическая выборка – при ранжировании генеральной совокупности устанавливается шаг отбора в зависимости от предполагаемого % отбора. Если совокупность не ранжирована, то это случайный отбор, т.е. по известным формулам.