ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 133
Скачиваний: 0
СОДЕРЖАНИЕ
Лекции по общей теории статистики
Тема 1. Введение. Предмет и метод статистической науки
1.1. История развития статистической науки
1.2. Предмет и метод статистической науки
1.3. Организация и функции статистических служб
Тема 2. Статистическое наблюдение
2.1. Статистическое наблюдение.
2.2. Сводка и группировка статистических данных
2.3. Принципы построения статистических группировок
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
3.3. Средние структурные величины
4.1. Понятие вариационных рядов.
Графическое отображение вариационных рядов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
5.2. Закон больших чисел и предельные теоремы
5.3 Формы организации выборочного наблюдения
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Оценка линейного коэффициента корреляции
7.2 Методы анализа тенденций рядов динамики
7.3. Статистические методы прогнозирования экономических показателей
8.2. Общие индексы количественных показателей
8.3. Общие индексы качественных показателей
8.4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов
![]() , (5.29)
, (5.29)
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Корреляционная связь (частный случай стохастической) – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами.
Задача корреляционного анализа – измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние.
Связь признаков проявляется в их согласованной вариации, при этом одни признаки выступают как факторные, а другие – как результативные. Причинно-следственная связь факторных и результативных признаков характеризуется по степени:
тесноты;
направлению;
аналитическому выражению.
6.2 Корреляционный анализ
Различают:
парную корреляцию – это зависимость между результативным и факторным признаком;
частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;
множественную – многофакторное влияние в статической модели
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции, который рассчитывается по одной из формул:
![]() (6.1)
(6.1)
![]() .
(6.2)
.
(6.2)
Оценка линейного коэффициента корреляции
|
Значение r |
Характер связи |
Интерпретация связи |
|
r = 0 |
Отсутствует |
Изменение x не влияет на изменения y |
|
0 < r < 1 |
Прямая |
С увеличением x увеличивается y |
|
-1 > r > 0 |
Обратная |
С увеличением x уменьшается y и наоборот |
|
r = 1 |
Функциональная |
Каждому значению факторного признака строго соответствует одно значение результативного |
Значимость
линейного
коэффициента корреляции проверяется
на основе t-критерия
Стьюдента. Для этого определяется
фактическое значение критерия
![]() :
:
![]() ,
(6.3)
,
(6.3)
Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
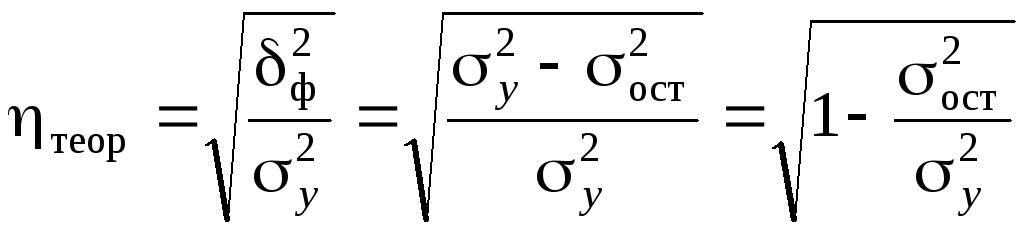 , (6.4)
, (6.4)
где ![]() –общая
дисперсия эмпирических
значений y,
характеризует вариацию результативного
признака за счет всех факторов, включая
х;
–общая
дисперсия эмпирических
значений y,
характеризует вариацию результативного
признака за счет всех факторов, включая
х;
![]() –факторная
дисперсия теоретических
значений результативного
признака, отражает влияние фактора х
на вариацию у;
–факторная
дисперсия теоретических
значений результативного
признака, отражает влияние фактора х
на вариацию у;
![]() –остаточная
дисперсия эмпирических
значений результативного
признака, отражает влияние на вариацию
у
всех остальных факторов кроме х.
–остаточная
дисперсия эмпирических
значений результативного
признака, отражает влияние на вариацию
у
всех остальных факторов кроме х.
По правилу сложения дисперсий:
![]() ,
т.е.
,
т.е.
Оценка связи на основе теоретического корреляционного отношения проходил по шкале Чэддока (тема 4).
Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = |r|.
Условие включения факторных признаков в регрессионную модель – наличие тесной связи между результативным и факторными признаками и как можно менее существенная связь между факторными признаками.
Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:
![]() ,
(6.7)
,
(6.7)
где R2
– коэффициент множественной детерминации
(R2
![]() );
);
k – число факторных признаков, включенных в уравнение регрессии.
Тема 7. Ряды динамики
7.1 Анализ динамических рядов
Динамический ряд представляет собой хронологическую последовательность числовых значений статистических показателей.
Виды рядов динамики (РД):
1) моментные (моментальные) РД;
2) интервальные РД;
3) РД с нарастающими итогами;
4) производные РД.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности.
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями в результатах развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяца, квартала, года и т.д.).
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные.
Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики:
характеристика уровней развития изучаемых явлений во времени;
измерение динамики изучаемых явлений посредством системы статистических показателей;
выявление и количественная оценка основной тенденции развития (тренда);
изучение периодических колебаний;
экстраполяция и прогнозирование.
Таблица 7.1 Уровни (показатели) ряда динамики
|
|
Показатель |
Формула |
|
Базисные |
Абсолютный прирост |
Δ |
|
Темп роста |
|
|
|
Темп прироста |
|
|
|
Цепные |
Абсолютный прирост |
Δ |
|
Темп роста |
|
|
|
Темп прироста |
|
|
|
Абсолютное значение 1% прироста |
|
|
|
Средние |
Абсолютный прирост |
|
|
Темп роста |
|
|
|
Темп прироста |
|
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
Средний уровень интервального ряда определяется по формуле средней арифметической простой:
![]() , (7.11)
, (7.11)
где n – число уровней.
В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:
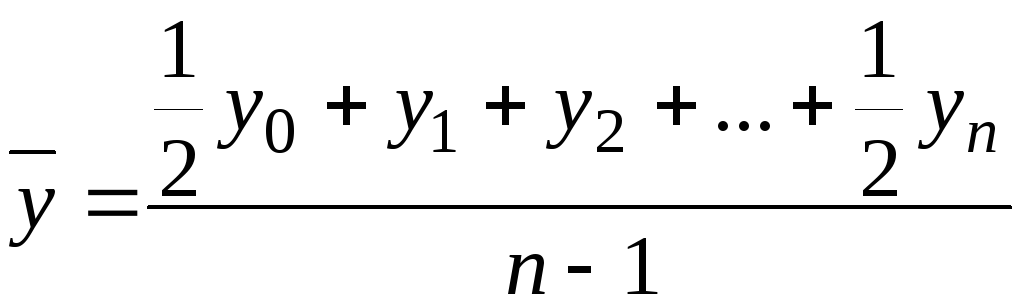 . (7.12)
. (7.12)
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:
![]() , (7.13)
, (7.13)
где уi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti.
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
![]() ;
;
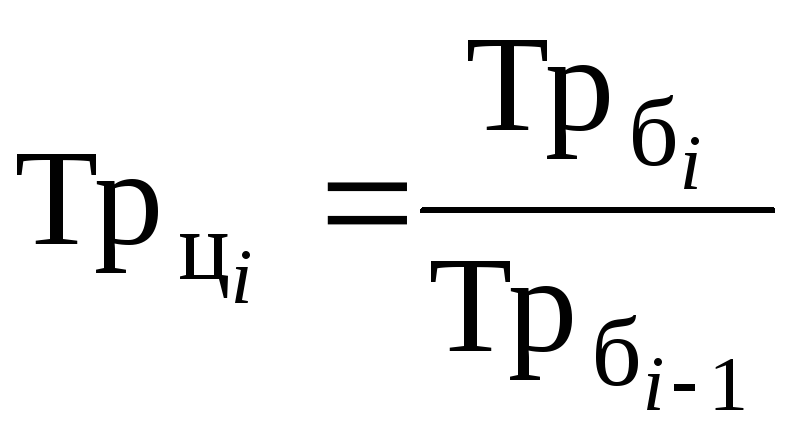 . (7.14)
. (7.14)
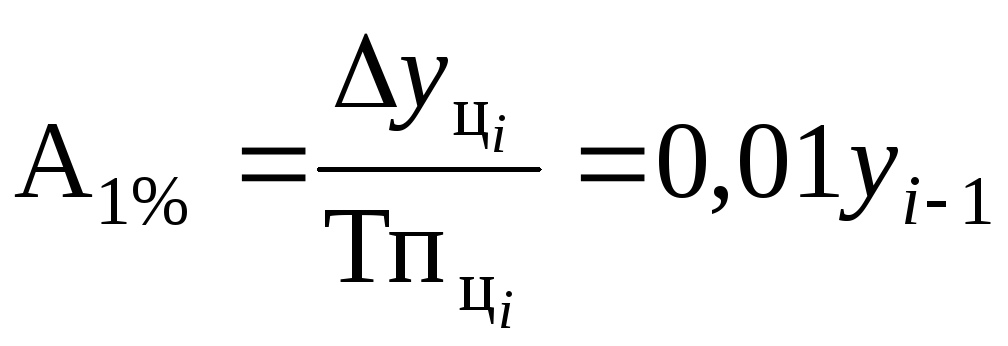 (7.7)
(7.7)