ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.03.2024
Просмотров: 125
Скачиваний: 0
СОДЕРЖАНИЕ
Лекции по общей теории статистики
Тема 1. Введение. Предмет и метод статистической науки
1.1. История развития статистической науки
1.2. Предмет и метод статистической науки
1.3. Организация и функции статистических служб
Тема 2. Статистическое наблюдение
2.1. Статистическое наблюдение.
2.2. Сводка и группировка статистических данных
2.3. Принципы построения статистических группировок
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
3.3. Средние структурные величины
4.1. Понятие вариационных рядов.
Графическое отображение вариационных рядов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
5.2. Закон больших чисел и предельные теоремы
5.3 Формы организации выборочного наблюдения
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Оценка линейного коэффициента корреляции
7.2 Методы анализа тенденций рядов динамики
7.3. Статистические методы прогнозирования экономических показателей
8.2. Общие индексы количественных показателей
8.3. Общие индексы качественных показателей
8.4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов
7.2 Методы анализа тенденций рядов динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. Методы выявления тренда:
1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
2) Метод скользящей средней заключается в том, что исчисляется средней уровень из определенного числа (обычно нечетного) первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы “скользит” по ряду динамики, передвигаясь на один срок.
Сглаженный ряд урожайности по трехлетиям короче фактического на один элемент ряда в начале и в конце ряда.
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени.
Общая тенденция развития рассчитывается как функция времени:
ŷt = f(t), (7.15)
где ŷt – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней ŷt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a0, a1 – параметры уравнения; t – время):
Линейная функция (прямая) ŷt = a0 + a1·t. (7.16)
Показательная
функция ![]() . (7.17)
. (7.17)
Степенная функция (парабола) ŷt = a0 + a1·t + a2·t2. (7.18)
7.3. Статистические методы прогнозирования экономических показателей
Прогнозирование – процесс определения возможных в будущем значений экономических показателей на основании уже известных.
Различают прогнозы по периоду упреждения: оперативные (до 1 мес.); краткосрочные (до 1 года); среднесрочные (1 – 5 лет); долгосрочные (более 5 лет).
Различают методы прогнозирования:
Экстраполяция тенденций:
- упрощенные приемы, основанные на средних показателях динамики (средние темпы роста, прироста);
- аналитические методы (метод наименьших квадратов, тренды, т.е. математические функции);
- адаптивные методы, учитывающие степень устаревания данных (методы скользящих и экспоненциальных средних, методы авторегрессии).
Методы статистического моделирования:
- статические (методы парной и множественной регрессии);
- динамические (анализ динамических рядов):
- методы агрегатного моделирования (разложение ряда на тенденции, сезонность, случайные составляющие);
- методы регрессии по взаимосвязанным рядам динамики (включаются в модель не только факторы, но и лаговые переменные);
- методы регрессии по пространственно-временной информации (для каждого ряда строится регрессионная модель по совокупности объектов).
Тема 8. Индексы
8.1. Сущность и виды индексов
Индексом в статистике называется относительный показатель, характеризующий изменение величины какого-либо явления по сравнению с эталоном.
Таблица 8.1. – Классификация индексов
|
Классификационный признак |
Вид индексов |
|||
|
1. Содержание изучаемых объектов |
Количественные (объемные) индексы (физического объема, товарооборота национального дохода) |
Качественные индексы (интенсивности) (курса валют, цен, себестоимости, производительности труда) |
||
|
2. Степень охвата элементов совокупности |
Индивидуальные (изменение одного показателя однотоварного) |
общие (групповые или субидексы (по отраслям)) |
||
|
3. Метод расчета |
Агрегатные |
Средние |
||
|
4. База сравнения |
Динамические |
Территориальные (например, индекс цен на товары в РФ и ФРГ) |
||
|
5. Вид весов |
С постоянными весами |
С переменными весами |
||
|
6. Состав явления |
Постоянного состава |
Переменного состава |
Структурных сдвигов |
|
|
7. Период исчисления |
Годовые |
Квартальные |
Помесячные и т.д. |
|
Таблица 8.2. – Обозначения индексируемых величин
|
Обозначение |
Индексируемая величина |
|
Обозначение |
Индексируемая величина |
|
q |
количество (объем) какого-либо товара в натуральном выражении |
|
t |
затраты времени на производство единицы продукции, трудоемкость |
|
p |
цена единицы товара |
|
W |
выработка продукции в единицу времени или на одного работника (производительность труда) |
|
pq |
товарооборот (стоимость продукции) |
|
||
|
z (c) |
себестоимость единицы продукции |
|
T=tq |
общие затраты времени на производство продукции или численность работников |
|
y |
урожайность отдельных сельскохозяйственных культур |
|
||
|
П |
посевная площадь под отдельными культурами |
|
8.2. Общие индексы количественных показателей
Индекс физического объема продукции показывает относительное изменение стоимости продукции из-за изменения объема производства.
Индивидуальный
индекс: ![]() ,
(8.1)
,
(8.1)
Агрегатный индекс:
![]() , (8.2)
, (8.2)
где q1 и q0 – объем выпуска продаж в базисном и отчетном периодах соответственно;
p0 – цена в базисном периоде.
Индекс товарооборота (или стоимости продукции), показывает во сколько раз изменилась стоимость продукции.
Агрегатный индекс товарооборота
![]() . (8.3)
. (8.3)
На сколько изменилась стоимость продукции показывает разница между числителем и знаменателем индекса:
![]() . (8.4)
. (8.4)
При построении индекса физического объема продукции в качестве соизмерителей (весов) принимаются сопоставимые, неизменные, фиксированные цены, отличающиеся от текущих (действующих) цен (это в условиях инфляции могут быть цены предшествующего периода) или себестоимость продукции z0. В этом случае индекс характеризует изменение издержек производства.
![]() . (8.5)
. (8.5)
Аналогично строятся индексы товарооборота и потребления.
Значение общего индекса Ipq зависит от изменения двух индексируемых величин объема продукции (q0, q1) и цен (p1,p0).
В зависимости от вида исходных данных можно исчислить средние взвешенные (арифметические) индексы физического объема.
Если
неизвестно q1,
но дано значение q0
и
![]() ,
а также стоимость продукции базисного
периодаp0,
то средний
арифметический индекс физического
объема равен:
,
а также стоимость продукции базисного
периодаp0,
то средний
арифметический индекс физического
объема равен:
![]() . (8.6)
. (8.6)
Средний
гармонический индекс физического объема
используется для аналитических оценок
в случае, когда неизвестно q0,
но дано значение q1
и
![]() ,
а также стоимость продукции базисного
периодаp0:
,
а также стоимость продукции базисного
периодаp0:
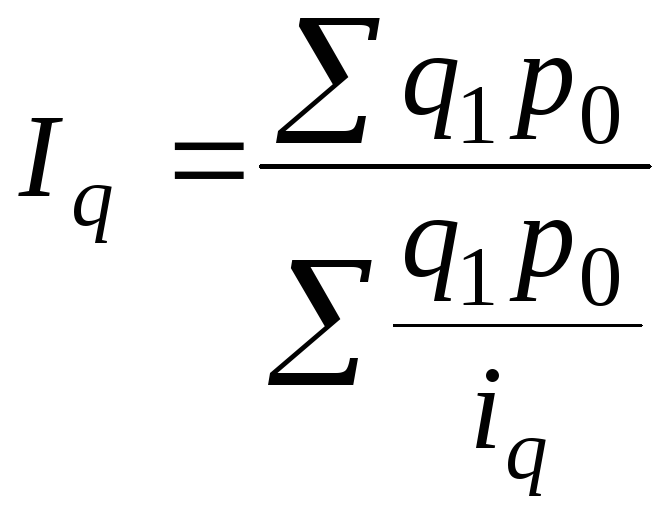 . (8.7)
. (8.7)
Индекс физического объема в прошлом вычисляется в сопоставимых, фиксированных ценах и отражает динамику выпуска продукции. В торговле чаще вычисляется в фактических ценах, отражая одновременное изменение цен и объема.