ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.07.2024
Просмотров: 20
Скачиваний: 0
ОТВЕТЫ (Глава 1)
1. См. черт. 54. 2. Указание. Уравнение х = 2 эквивалентно двум уравнениям: x = — 2 и x = 2; соответственно имеем две точки A1(—2) и A1 (2) (черт. 54а). Уравнение | х—1| = 3 эквивалентно двум уравнениям
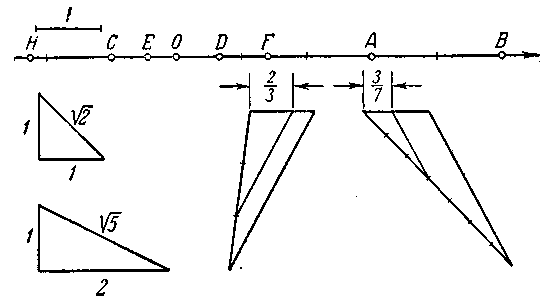
Черт. 54.
х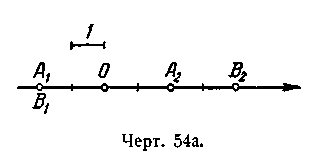 —
1= — 3 и x
— 1=3, откуда находим х
= — 2 и x
= 4 и соответствующие им точки B1
и B2
(черт. 54а). В остальных случаях решения
аналогичны. 3. Точки расположены: 1) Справа
от точки М1
(2); 2) слева от точки М2
(3), включая точку М2
3) справа от точки М3(12);
4) слева от точки М4(
—
1= — 3 и x
— 1=3, откуда находим х
= — 2 и x
= 4 и соответствующие им точки B1
и B2
(черт. 54а). В остальных случаях решения
аналогичны. 3. Точки расположены: 1) Справа
от точки М1
(2); 2) слева от точки М2
(3), включая точку М2
3) справа от точки М3(12);
4) слева от точки М4(![]() ),
включая точку Л44;
5) справа от точки М5(
),
включая точку Л44;
5) справа от точки М5(![]() ),
6) внутри отрезка, ограниченного точками
М6(1)
и М2(3);
7) внутри отрезка, ограниченного точками
М7(—
2) и М2(3),
включая точки М7,
и М2;
8) внутри отрезка, ограниченного точками
А(1)
и В(2);
9) вне отрезка, ограниченного точками
Р(—
1) и Q(2);
10) вне отрезка, ограниченного точками
А(1)
и В(2);
11) внутри отрезка, ограниченного
точками Р(— 1)
и Q(2);
12) внутри отрезка,
ограниченного N
; 13) вне отрезка, ограниченного точками
M(3)
и N(5);
14) вне отрезка, ограниченного точками
P1(—4)
и Q1(3);
15) внутри
отрезка,
ограниченного точками P1(—
4) и
Q1
(3), включая точки P1
и Q1.
4.
1) AB=
8, |AB|
= 8; 2) АВ = — 3,
AB=
3; 3) AB
= 4, |AB|
= 4; AB
= 2, |AB|
=2; 5) AB
= —2, |AB|
= 2; 6) AB
= 2, |AB|
= 2. 5.
1) —2; 2) 5; 3) 1; 4) —8; 5) — 2 и 2; 6) — 1 и 5; 7) —6 и
4; 8) —7 и —3. 6.
1) Внутри отрезка, ограниченного точками
A(—1)
и B(1);
2) вне отрезка, ограниченного точками A
(—2) и В (2);
3) внутри отрезка, ограниченного точками
A
(— 2) и B
(2), включая точки A
и B;
4) вне отрезка, ограниченного точками A
(— 3) и B
(3). включая точки A
и 5; 5) внутри отрезка, ограниченного
точками A
(—1) и B
(5); 6) внутри отрезка, ограниченного
точками A
(4) и В (6),
включая точки A
и В; 7)
вне
),
6) внутри отрезка, ограниченного точками
М6(1)
и М2(3);
7) внутри отрезка, ограниченного точками
М7(—
2) и М2(3),
включая точки М7,
и М2;
8) внутри отрезка, ограниченного точками
А(1)
и В(2);
9) вне отрезка, ограниченного точками
Р(—
1) и Q(2);
10) вне отрезка, ограниченного точками
А(1)
и В(2);
11) внутри отрезка, ограниченного
точками Р(— 1)
и Q(2);
12) внутри отрезка,
ограниченного N
; 13) вне отрезка, ограниченного точками
M(3)
и N(5);
14) вне отрезка, ограниченного точками
P1(—4)
и Q1(3);
15) внутри
отрезка,
ограниченного точками P1(—
4) и
Q1
(3), включая точки P1
и Q1.
4.
1) AB=
8, |AB|
= 8; 2) АВ = — 3,
AB=
3; 3) AB
= 4, |AB|
= 4; AB
= 2, |AB|
=2; 5) AB
= —2, |AB|
= 2; 6) AB
= 2, |AB|
= 2. 5.
1) —2; 2) 5; 3) 1; 4) —8; 5) — 2 и 2; 6) — 1 и 5; 7) —6 и
4; 8) —7 и —3. 6.
1) Внутри отрезка, ограниченного точками
A(—1)
и B(1);
2) вне отрезка, ограниченного точками A
(—2) и В (2);
3) внутри отрезка, ограниченного точками
A
(— 2) и B
(2), включая точки A
и B;
4) вне отрезка, ограниченного точками A
(— 3) и B
(3). включая точки A
и 5; 5) внутри отрезка, ограниченного
точками A
(—1) и B
(5); 6) внутри отрезка, ограниченного
точками A
(4) и В (6),
включая точки A
и В; 7)
вне
Черт. 55. Черт. 56.
отрезка, ограниченного
точками А(— 1)
и 5(3), включая точки А
и B;
8) вне отрезка, ограниченного точками A
(2) и B
(4), включая точки A
и B;
9) внутри отрезка, ограниченного точками
A
(—4) и B
(2); 10) вне отрезка, ограниченного точками
A(—3)
и В(— 1);
11) внутри отрезка, ограниченного точками
A(—6)
и В(—4),
включая точки А и В;
12) вне отрезка,
ограниченного точками A(—3)
и В(—4), включая
точки A
и В. 7.
1; 2) —![]() ;
3) 2; 4)
;
3) 2; 4)
![]() ;
5)
;
5)
![]()
![]() ,
8.
,
8.
![]()
![]() =
=
![]()
![]() 2=
2=
![]()
![]() 3=
3=
![]()
![]() 4=
4=
![]()
![]() 5=
5=
![]()
![]() 6=
6=
![]() 9.
9.
![]() =
=
![]() 10. x
=
10. x
=
![]() 11. x
=
11. x
=
![]() 12. 1) 4; 2; 3) —2; 4) —2; 5)
12. 1) 4; 2; 3) —2; 4) —2; 5)
![]() .
13.1)
.
13.1)
![]() ;
2)
;
2)
![]() 3)
3)
![]() ;
4) 7; 5) 3; 6) 0. 14.
1) М (—
11); 2) N
(13). 15.
(5) и (12). 16.
A(7) и
B(—41). 17.
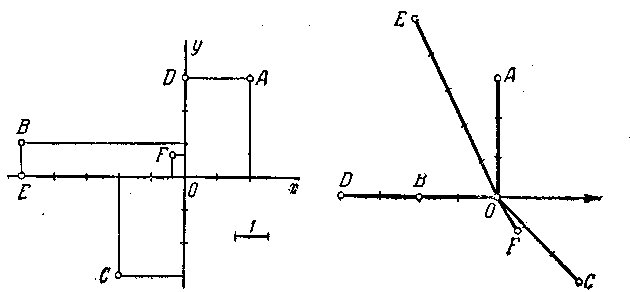
См. черт. 55. 18.
Ах(2;
0), Bc(3;0),
Сx(—5;
0), Dx(—3;0);
Ех(—5;
0). 19.
Ay(0;
2), Вy(0;
1), Сy(0;
— 2), Dy(0,
1), Еy(0;
—2). 20.
1) (2; —3); 2) (—3; —2); 3) (—1; 1); 4) (—3; 5); 5) (—
4; —6); 6) (а;
—b).
21.
1) (1; 2); 2) (—3; — 1); 3) (2; —2); 4) (2; 5); 5) (—3; —5);
6) (—а; b).
22. 1)
(—3; —3); 2) (—2; 4); 3) (2;—1); 4) (—5; 3); 5) (5; 4); 6)
(—а; — b).
23.
1) (3; 2); 2) (—2; 5); 3) (4; —3). 24.
1) (—5; —3); 2) (—3; 4); 3)
(2; —7). 25.
1) В первой и третьей; 2) во второй и
четвёртой; 3) в первой и третьей; 4) во
второй и четвёртой; 5) в первой, второй
и четвёртой; 6) во второй, третьей и
четвёртой; 7) в первой, третьей и четвёртой;
8) в первой, второй и третьей.
26. См. черт. 56. 27.
(2; -
;
4) 7; 5) 3; 6) 0. 14.
1) М (—
11); 2) N
(13). 15.
(5) и (12). 16.
A(7) и
B(—41). 17.
См. черт. 55. 18.
Ах(2;
0), Bc(3;0),
Сx(—5;
0), Dx(—3;0);
Ех(—5;
0). 19.
Ay(0;
2), Вy(0;
1), Сy(0;
— 2), Dy(0,
1), Еy(0;
—2). 20.
1) (2; —3); 2) (—3; —2); 3) (—1; 1); 4) (—3; 5); 5) (—
4; —6); 6) (а;
—b).
21.
1) (1; 2); 2) (—3; — 1); 3) (2; —2); 4) (2; 5); 5) (—3; —5);
6) (—а; b).
22. 1)
(—3; —3); 2) (—2; 4); 3) (2;—1); 4) (—5; 3); 5) (5; 4); 6)
(—а; — b).
23.
1) (3; 2); 2) (—2; 5); 3) (4; —3). 24.
1) (—5; —3); 2) (—3; 4); 3)
(2; —7). 25.
1) В первой и третьей; 2) во второй и
четвёртой; 3) в первой и третьей; 4) во
второй и четвёртой; 5) в первой, второй
и четвёртой; 6) во второй, третьей и
четвёртой; 7) в первой, третьей и четвёртой;
8) в первой, второй и третьей.
26. См. черт. 56. 27.
(2; -![]() ),
(2;
),
(2;
![]() ),
(3;
),
(3;
![]() ),
(1; —2), (5; 1). 28. (1; —
),
(1; —2), (5; 1). 28. (1; —![]() ),
(5; —
),
(5; —![]() ),
(2;
),
(2;
![]() ),
(4; —
),
(4; —![]() ),
(3;
— 2). 29.
C(3;
),
(3;
— 2). 29.
C(3;
![]() ,)
и D(5;
—
,)
и D(5;
—![]() ).
30.
(1; —5). 31.
А(3;
—
).
30.
(1; —5). 31.
А(3;
—![]() ),
B(2;
),
B(2;
![]() ),
С(1;
0), D(5;
),
С(1;
0), D(5;
![]() ),
Е(3;
2—),
F(2;
—1).
32.
М1(3;
0), М2(1;
),
Е(3;
2—),
F(2;
—1).
32.
М1(3;
0), М2(1;
![]() ),
М3(2
—
),
М3(2
—![]() ),
M4(5;
—
),
M4(5;
—![]() ),
М5(3;
),
М6(1;
),
М5(3;
),
М6(1;
![]() ),
33.
(6;
),
33.
(6;
![]() ).
34.
d
=
).
34.
d
=
![]() 35.
d
= 7. 36.
9(17 — 4
35.
d
= 7. 36.
9(17 — 4![]() )
кв. ед. 37.
2 (13 + 6
)
кв. ед. 37.
2 (13 + 6![]() )
кв. ед. 38.
28
)
кв. ед. 38.
28![]() кв.
ед. 39.
S =
кв.
ед. 39.
S =
![]() 40.
5 кв.
ед.
41.
3(4
40.
5 кв.
ед.
41.
3(4![]() -
1) кв. ед. 42.
M1(0;
6), M2(5;
0), M3(
-
1) кв. ед. 42.
M1(0;
6), M2(5;
0), M3(![]() ),
M4(5;
— 5
),
M4(5;
— 5![]() ),
M5(—
4; 4
),
M5(—
4; 4![]() ),
M6(6
),
M6(6![]() ;
— 6). 43.
M1(5;
;
— 6). 43.
M1(5;
![]() ),
M2(3;
),
M3(2;
),
M2(3;
),
M3(2;
![]() ),
M
4(2; —
),
M
4(2; —![]() )
, M5(2;
—
)
, M5(2;
—![]() .
44.
1) 3; 2) —3; 3) 0; 4) 5; 5) —5; 6) 2. 47.
1) X=1,
Y = 3; 2)
X= —
4, Y
= —2; 3) X
= 1, Y
= —7; 4) X
= 5,_Y
= 3.
48.
(3; —1). 49.
(—3; 2). 52.
1) X=
— 6, Y
= 6
.
44.
1) 3; 2) —3; 3) 0; 4) 5; 5) —5; 6) 2. 47.
1) X=1,
Y = 3; 2)
X= —
4, Y
= —2; 3) X
= 1, Y
= —7; 4) X
= 5,_Y
= 3.
48.
(3; —1). 49.
(—3; 2). 52.
1) X=
— 6, Y
= 6![]() 2) X
= 3
2) X
= 3![]() ,
Y
= —3; 3) Х =
,
Y
= —3; 3) Х =
![]() ,
Y
= —
,
Y
= —
![]() .
53.
1) 5; 2) 13; 3) 10. 54.
1) d
= 2, θ
=
.
53.
1) 5; 2) 13; 3) 10. 54.
1) d
= 2, θ
=
![]() ;
2) d
= 6, θ
= —
;
2) d
= 6, θ
= —![]() ;
3) d
= 4, θ
=
;
3) d
= 4, θ
=
![]() ;.
55.
a)
d
=
;.
55.
a)
d
=
![]() ,
θ
= —
,
θ
= —![]() ;
б)
d
= 5, θ
= arctg
;
б)
d
= 5, θ
= arctg![]() ;
в)
d
=
13,
θ
= π
— arctg
;
в)
d
=
13,
θ
= π
— arctg![]() ;
г)
d
=
;
г)
d
=
![]() ,
θ
= — arctg
5.
56.
a) 3; б)
— 3. 57.
a) (—9; 3); б)
(—9; —7). 58.
a) (—15; —12); б)
(1; —12). 59.
—2. 60.
,
θ
= — arctg
5.
56.
a) 3; б)
— 3. 57.
a) (—9; 3); б)
(—9; —7). 58.
a) (—15; —12); б)
(1; —12). 59.
—2. 60.
![]() 61.
4. 62.
1) —5; 2) 5. 63.
1) 5; 2) 10; 3) 5; 4)
61.
4. 62.
1) —5; 2) 5. 63.
1) 5; 2) 10; 3) 5; 4)
![]() ;
5) 2
;
5) 2![]() ;
6) 13. 64.
137 кв.
ед.
65.
34 кв. ед. 66.
8
;
6) 13. 64.
137 кв.
ед.
65.
34 кв. ед. 66.
8
![]() кв. ед. 67.
13, 15. 68.
150 кв. ед. 69.
4
кв. ед. 67.
13, 15. 68.
150 кв. ед. 69.
4
![]() .
73.
< M2M1M3
— тупой. 75.
< ВАС =
45°, < АВС
= 45°, < АСB
= 90°. 76.
60°. Указание. Вычислить длины сторон
треугольника, а затем применить теорему
косинусов. 77.
M1(6;
0) и М2(—
2; 0). 78.
M1(0;
28) и M2(0;
— 2). 79.
Р
1(1; 0) и Р2(6;
0). 80. C1(2;
2), /?! = 2; С„(10; 10), /?s=10.
83.
С, (—3; — 5), С2
(5; — 5). 82.
Л1а
(3; 0). 83.
5(0; 4) и D(—1;
—3). 84.
Условию задачи удовлетворяют два
квадрата, симметрично расположенных
относительно стороны АВ.
Вершины одного квадрата
суть точки d
(— 5; 0), Д (— 2; — 4),
вершины другого — С2
(3; 6), А (6; 2). 85.
С(3; —2), /?==Ю. 86.
(1; —2). 87.
0(4; 6). 88.
Середины сторон АВ,
ВС, АС соответственно
суть (2; —4), (—1; 1), (—2; 2). 89.
1) М(\; 3);
2) JV(4;
—3). 90.
(1; —3), (3; 1) и (—5; 7). 91.
D(—
3; 1). 92.
(5; —3), (1; —5). 93.
D1
(2; 1), D1
(—2; 9), D3
(6; —3). Указание. Четвёртая вершина
параллелограмма может быть противоположной
любой из данных. Таким образом, условию
задачи удовлетворяют три параллелограмма.
94.13.
95.
(2;—1) и (3; 1). 96.
(
.
73.
< M2M1M3
— тупой. 75.
< ВАС =
45°, < АВС
= 45°, < АСB
= 90°. 76.
60°. Указание. Вычислить длины сторон
треугольника, а затем применить теорему
косинусов. 77.
M1(6;
0) и М2(—
2; 0). 78.
M1(0;
28) и M2(0;
— 2). 79.
Р
1(1; 0) и Р2(6;
0). 80. C1(2;
2), /?! = 2; С„(10; 10), /?s=10.
83.
С, (—3; — 5), С2
(5; — 5). 82.
Л1а
(3; 0). 83.
5(0; 4) и D(—1;
—3). 84.
Условию задачи удовлетворяют два
квадрата, симметрично расположенных
относительно стороны АВ.
Вершины одного квадрата
суть точки d
(— 5; 0), Д (— 2; — 4),
вершины другого — С2
(3; 6), А (6; 2). 85.
С(3; —2), /?==Ю. 86.
(1; —2). 87.
0(4; 6). 88.
Середины сторон АВ,
ВС, АС соответственно
суть (2; —4), (—1; 1), (—2; 2). 89.
1) М(\; 3);
2) JV(4;
—3). 90.
(1; —3), (3; 1) и (—5; 7). 91.
D(—
3; 1). 92.
(5; —3), (1; —5). 93.
D1
(2; 1), D1
(—2; 9), D3
(6; —3). Указание. Четвёртая вершина
параллелограмма может быть противоположной
любой из данных. Таким образом, условию
задачи удовлетворяют три параллелограмма.
94.13.
95.
(2;—1) и (3; 1). 96.
(![]() ;
—2). 97.
;
—2). 97.
![]() .
98.
(- 11; -3 ). 99.
4. 100.
.
98.
(- 11; -3 ). 99.
4. 100.
![]() =
2;
=
2;
![]() ;
;
![]() ;
101.
A(3;
—1) и B
(0, 8). 102.
(3; —1). 103.
(4; —5). 104.
(—9; 0). 105.
(0; —3). 106.
1:3, считая от точки В.
107.
(
;
101.
A(3;
—1) и B
(0, 8). 102.
(3; —1). 103.
(4; —5). 104.
(—9; 0). 105.
(0; —3). 106.
1:3, считая от точки В.
107.
(![]() ;
1). 108.
х =
;
1). 108.
х =![]() ;
y
=
;
y
=![]() ;
109.
M(—l;
0), С(0;2).
111.
(5; 5). 112. (
;
109.
M(—l;
0), С(0;2).
111.
(5; 5). 112. (![]() .
113.
(
.
113.
(![]() .
114.
x=
.
114.
x=![]() ,
y=
,
y=![]() .
115.
(4; 2). У к а з а н и е. Вес однородной
проволоки пропорционален её длине. 116.
1) 14 кв. ед.; 2) 12 кв. ед.; 3) 26 кв. ед.
117. 5. 118.
20 кв. ед. 119.
7,4. 120.
х=
.
115.
(4; 2). У к а з а н и е. Вес однородной
проволоки пропорционален её длине. 116.
1) 14 кв. ед.; 2) 12 кв. ед.; 3) 26 кв. ед.
117. 5. 118.
20 кв. ед. 119.
7,4. 120.
х=
![]() ,
у = 4
,
у = 4![]() .
121.
х =
.
121.
х =![]() ,
y=3
,
y=3![]() .
122.
(0; — 8) или (0; — 2). 123.
(5; 0) или (—
.
122.
(0; — 8) или (0; — 2). 123.
(5; 0) или (—![]() ;0).
124.(5;2)
или (2; 2). 125.
C1(—
7; —3), D1(—6;
—4) или С2
(17; —3),
D2
(18; —4). 126.
С1
(—2; 12), D1
(—5; 16) или С2(—
2;
;0).
124.(5;2)
или (2; 2). 125.
C1(—
7; —3), D1(—6;
—4) или С2
(17; —3),
D2
(18; —4). 126.
С1
(—2; 12), D1
(—5; 16) или С2(—
2;
![]() ),
D2
(—5;
),
D2
(—5;
![]() .
127.
1) х =x'
+ 3, у=у' +
4; 2)х — х' — 2,
y
— y
+ 1; 3)x
= x'
—3, у = y'
+5, 128.
A
(4; —1), 5(0; —4), С (2; 0). 129.
1) A(0;
0), В (— 3;
2), С (—4; 4); 2) A
(3; — 2), В (0;
0), С (— 1; 2); 3) A
(4; — 4), В (1;
— 2), C
(0; 0). 130.
1) (3; 5); 2) (—2; 1); 3) (0; — 1); 4) (—5; 0). 131.
1) х =
.
127.
1) х =x'
+ 3, у=у' +
4; 2)х — х' — 2,
y
— y
+ 1; 3)x
= x'
—3, у = y'
+5, 128.
A
(4; —1), 5(0; —4), С (2; 0). 129.
1) A(0;
0), В (— 3;
2), С (—4; 4); 2) A
(3; — 2), В (0;
0), С (— 1; 2); 3) A
(4; — 4), В (1;
— 2), C
(0; 0). 130.
1) (3; 5); 2) (—2; 1); 3) (0; — 1); 4) (—5; 0). 131.
1) х =![]() ,
y
=
,
y
=![]() ;
х =
;
х =![]() ;
y
=
;
y
=![]() 3)
x=
- у'; y=
- x'
4) x=
- у', yx=
- x'.
5) x
= — x',
y
= — y'.
132. A(
3)
x=
- у'; y=
- x'
4) x=
- у', yx=
- x'.
5) x
= — x',
y
= — y'.
132. A(![]() ;
l), B(
;
l), B(![]() ;
;![]() ),
C(3; —
),
C(3; —![]() ).
133.
1) М
(
).
133.
1) М
(![]() ;
;
![]() ),
N(— 3
),
N(— 3![]() ; 2
; 2![]() ),
Р(—
),
Р(—
![]() ;
—
;
—
![]() );
2) M (1; —3), N (5; 1), Р
(—1; 3); 3) М
(—1; 3), N
(—5; —1),
Р(1;—3);
4) М(—3;
—1), N
(1; —
5), Р
(3; 1). 134.
1) 60°; 2) —30°. 135.
О'(2; —4). 136.
х = х' +1,у = у'—3. 137.
х =
);
2) M (1; —3), N (5; 1), Р
(—1; 3); 3) М
(—1; 3), N
(—5; —1),
Р(1;—3);
4) М(—3;
—1), N
(1; —
5), Р
(3; 1). 134.
1) 60°; 2) —30°. 135.
О'(2; —4). 136.
х = х' +1,у = у'—3. 137.
х =
![]() x'
+
x'
+
![]() у',
y=—
у',
y=—![]() x'
+
x'
+
![]() y'.
138.
M1
(1; 5), M2(2;
0), М3
(16; —5). 139.
A (6; 3), B (0; 0), С
(5; —10). 140.
1) О' (3; —2),
y'.
138.
M1
(1; 5), M2(2;
0), М3
(16; —5). 139.
A (6; 3), B (0; 0), С
(5; —10). 140.
1) О' (3; —2),
![]() ==90°;
2) O'(—
1; 3),
==90°;
2) O'(—
1; 3),
![]() =180°;
3) О' (5;
— 3),
=180°;
3) О' (5;
— 3),
![]() =
— 45°. 141.
x
=
=
— 45°. 141.
x
=![]() —
—![]() +9,
+9,
![]() .
142.
M1
(1; 9), М2
(4;2),М3
(1;—3), М4
(0;3 +
.
142.
M1
(1; 9), М2
(4;2),М3
(1;—3), М4
(0;3 +
![]() ),
М5
(1 +
),
М5
(1 +
![]() ;
1). 143.
M1(0;5),
M2
(3;0), M3(—1;0),
M4(0;—6),
М5
(
;
1). 143.
M1(0;5),
M2
(3;0), M3(—1;0),
M4(0;—6),
М5
(![]() ;
1). 144.
M1
(2; 0), M2(l;—
;
1). 144.
M1
(2; 0), M2(l;—![]() ),
М3
(3;
),
М3
(3;
![]() )
, M4
(2;
)
, M4
(2;
![]() ),
M5
(2;
),
M5
(2;
![]() ).
145.
M1(
).
145.
M1(![]() ;
;
![]() ),
M2
(2;
),
M2
(2;
![]() ),
M3
(2;
),
M3
(2;
![]() ),
M4
(2;
),
M4
(2;
![]() ),
M5
(4;
),
M5
(4;
![]() ).
).