ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.07.2024
Просмотров: 19
Скачиваний: 0
ОТВЕТЫ (Глава 2)
146. f(x, у) =2ах—а2. 147. 1) f (x; у) = 2ах; 2) f (x, у) = —2ax — а2. 148. f(x, у) = 4x2 + 4у2 + 2а2. 149. f (x, у) = 4x2 + 4y2 — 4ах — 4ау + 4а2. 150. f (х, у) = х2 + y2 — 25. 151. f (х, у) = 2ху— 16. 152. При повороте координатных осей выражение функции не меняется. 153. (3; 1). 154. Такой точки не существует. 155. ±45° или ± 135°. 156. 30°, 120°, —60°, — 150°. 157. Точки M1, M4 и M5 лежат на линии; точки Мг, М3 , и Мв не лежат на ней. Уравнение определяет биссектрису второго и четвёртого координатных углов (черт. 57). 158. а) (0; — 5), (0; 5); б) (—3; —4), (—3; 4); в) (5; 0); г) на данной линии такси точки нет; д) (— 4; 3), (4; 3); е) (0; — 5); ж) на данной линии такой точки нет. Уравнение определяет окружность с центром О (0; 0) и радиусом 5 (черт. 58). 159. 1) Биссектриса первого и третьего координатных углов; 2) биссектриса второго и четвёртого координатных углов; 3) прямая, параллельная оси Оу, отсекающая на положительной полуоси Ох, считая от начала координат, отрезок, равный 2 (черт. 59); 4) прямая, параллельная оси Оу, отсекающая на отрицательной полуоси Ох, считая от начала координат, отрезок, равный 3 (черт. 59); 5) прямая, параллельная оси Ох, отсекающая на положительной полуоси Оу, считая от начала координат, отрезок, равный 5 (черт. 59); 6) прямая, параллельная оси Ох, отсекающая на отрицательной полуоси Оу, считая от начала координат, отрезок, равный 2 (черт. 59); 7) прямая, совпадающая с осью ординат; 8) прямая, совпадающая с осью абсцисс; 9) линия
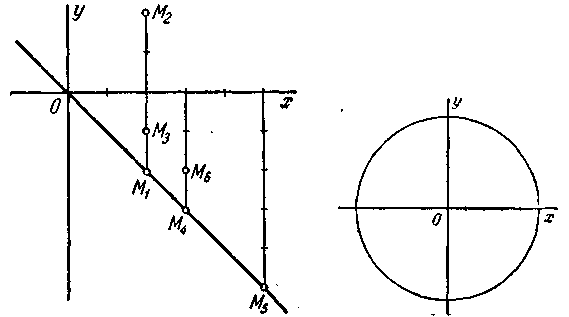
Черт. 57. Черт. 58.
состоит из двух прямых: биссектрисы первого и третьего координатных углов и прямой, совпадающей с осью ординат; 10) линия состоит из двух прямых: биссектрисы второго и четвёртого координатных углов и прямой, совпадающей с осью абсцисс; 11) линия состоит из двух биссектрис координатных углов (черт. 60); 12) линия состоит из двух прямых: прямой, совпадающей с осью
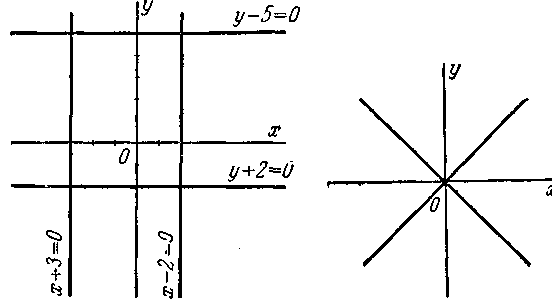
Черт. 59. Черт. 60.
абсцисс, и прямой, совпадающей с осью ординат; 13) линия состоит из двух прямых, параллельных оси абсцисс, которые отсекают на оси ординат, считая от начала координат, отрезки, равные 3 и —3 (черт. 61); 14) линия состоит из двух прямых, параллельных оси Оу, которые отсекают на положительной полуоcи Ох, считая от начала координат, отрезки, равные 3 и 5 (черт. 62); 15) линия состоит из двух прямых, параллельных оси Ох, которые отсекают на отрицательной полуоси Оу, считая от начала координат, отрезки, равные 1 и 4 (черт. 63); 16) линия состоит из трёх прямых: прямой, совпадающей с осью абсцисс, и двух прямых, параллельных оси ординат, которые отсекают на положительной полуоси абсцисс, считая от начала координат, отрезки, равные
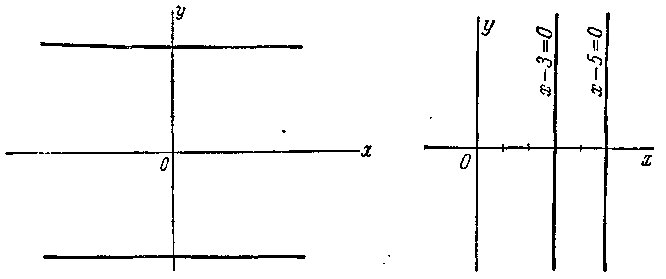
Черт. 61. Черт. 62.
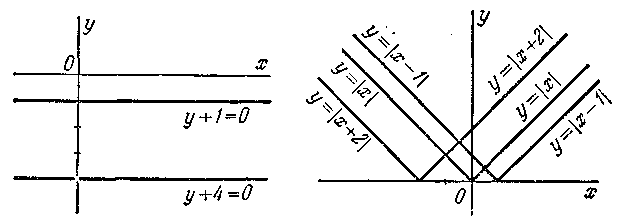
` Черт. 63. Черт. 64.
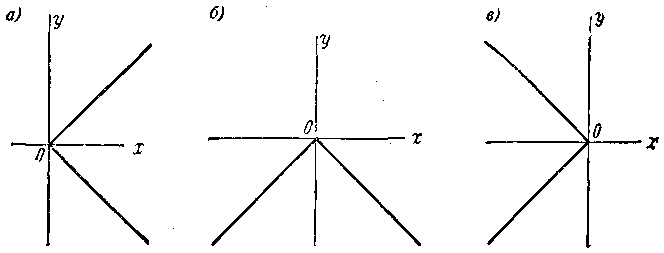
Черт. 65.
2 и 5; 17) линия состоит из двух лучей: биссектрис первого и второго координатных углов (черт. 64); 18) линия состоит из двух лучей: биссектрис первого и четвёртого координатных углов (черт 65, а); 19) линия состоит из двух лучей: биссектрис третьего и четвертого координатных углов (черт. 65, а); 20) линия состоит из двух лучей: биссектрис второго и третьего координатных углов (черт. 65,8); 21) линия состоит из двух лучей, расположенных в верхней полуплоскости, выходящих из точки (1; 0) и направленных параллельно биссектрисам координатных углов (черт. 64); 22) линия состоит из двух лучей,
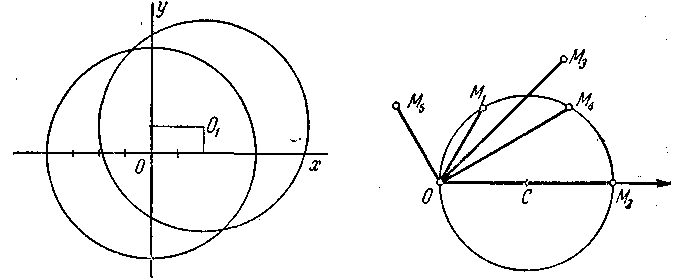
Черг. 66. Черт. 67.
расположенных в верхней полуплоскости, выходящих из точки (— 2; 0) и направленных параллельно биссектрисам координатных углов (черт. 64); 23) окружность с центром в начале координат и радиусом 4 (черт. 66); 24) окружность с центром O1 (2; 1) и радиусом 4 (черт. 66); 25) окружность с центром
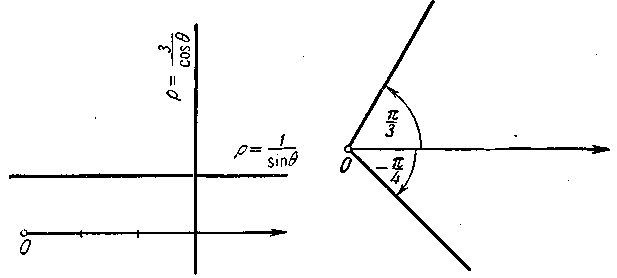
Ч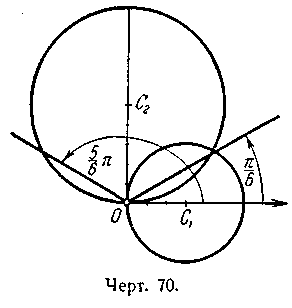 ерт.
68. Черт. 69.
ерт.
68. Черт. 69.
(—5; 1) и радиусом 3; 26) окружность
с центром (1; 0) и радиусом 2; 27) окружность
с центром (0; — 3) и радиусом 1; 28) линия
состоит из одной точки (3; 0) — вырожденная
линия; 29) линия состоит из одной точки
(0; 0) — вырожденная линия; 30) нет ни
одной точки, координаты которой
удовлетворяли бы данному уравнению
(«мнимая линия»); 31) нет ни одной точки,
координаты которой удовлетворяли
бы данному уравнению («мнимая линия»).
160.
Линии 1), 2) и 4) проходят через начало
координат. 161.
1) а) (7; 0), (—7; 0); б) (0; 7), (0; —7); 2) а) (0; 0), (6;
0); б) (0; 0), (0; —8); 3) а) (— 10; 0), (— 2; 0); б) линия
с осью Оу не
пересекается; 4) линия с координатными
осями не пересекается; 5) а) (0; 0), (12; 0); б)
(0; 0), (0; —16); 6) а) линия с осью Ох
не пересекается; б)
(0; —1), (0; —7); 7) линия с координатными
осями не пересекается.
162. 1) (2; 2), (— 2; — 2); 2)
(1; — 1), (9; — 9); 3) (3; — 4), (1
![]() ;
—4
;
—4![]() );
4) линии не пересекаются. 163.
Точки М1
М2
и М4
лежат на данной линии; точки M3
и М5
не лежат на ней.
Уравнение определяет окружность (черт.
67). 164.
а) (6;
);
4) линии не пересекаются. 163.
Точки М1
М2
и М4
лежат на данной линии; точки M3
и М5
не лежат на ней.
Уравнение определяет окружность (черт.
67). 164.
а) (6;
![]() );
б) (6; —
);
б) (6; —![]() ) ; в) (3; 0); г) (2
) ; в) (3; 0); г) (2![]() ;
;
![]() )
; прямая, перпендикулярная
к полярной оси и отсекающая на ней,
считая от полюса, отрезок, равный 3 (черт.
688).
165.
а) (1;
)
; прямая, перпендикулярная
к полярной оси и отсекающая на ней,
считая от полюса, отрезок, равный 3 (черт.
688).
165.
а) (1;![]() );
б) (2;
);
б) (2;
![]() )
и (2;
)
и (2;
![]() );
в) (
);
в) (![]() ;
;
![]() )
и (
)
и (![]() ;
;
![]() );
прямая, расположенная
в верхней полуплоскости, параллельная
полярной оси и отстоящая от неё на
расстоянии 1 (черт. 68). 166.
1) Окружность с центром в полюсе и
радиусом 5; 2) луч, выходящий из полюса,
наклонённый к 2полярной оси под
углом
);
прямая, расположенная
в верхней полуплоскости, параллельная
полярной оси и отстоящая от неё на
расстоянии 1 (черт. 68). 166.
1) Окружность с центром в полюсе и
радиусом 5; 2) луч, выходящий из полюса,
наклонённый к 2полярной оси под
углом![]() (черт.
69); 3) луч, выходящий из полюса, наклонённый
к полярной оси под углом —
(черт.
69); 3) луч, выходящий из полюса, наклонённый
к полярной оси под углом —
![]() (черт. 69); 4) прямая, перпендикулярная
к полярной оси, отсекающая на ней, считая
от полюса, отрезок а = 2; 5) прямая,
расположенная в верхней полуплоскости,
параллельная полярной оси, отстоящая
от неё на расстоянии, равном 1; 6) окружность
с центром C1
(3; 0) и ра2диусом 3 (черт. 70); 7) окружность
с центром С2
(5;
(черт. 69); 4) прямая, перпендикулярная
к полярной оси, отсекающая на ней, считая
от полюса, отрезок а = 2; 5) прямая,
расположенная в верхней полуплоскости,
параллельная полярной оси, отстоящая
от неё на расстоянии, равном 1; 6) окружность
с центром C1
(3; 0) и ра2диусом 3 (черт. 70); 7) окружность
с центром С2
(5;
![]() )
и радиусом 5 (черт.
70); 8) линия состоит
)
и радиусом 5 (черт.
70); 8) линия состоит
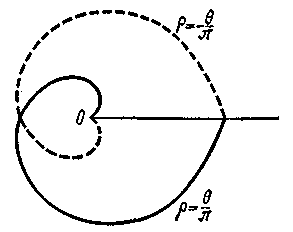
Черт. 71. Черт. 72.
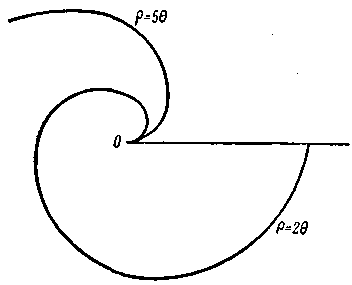
из двух лучей, выходящих из
полюса, один из которых наклонён к
полярной оси под углом
![]() ,
,
а другой — под углом
![]() (черт.
70); 9) линия состоит из концентрических
окружностей с центром в полюсе,
радиусы которых r
определяются по формуле
(черт.
70); 9) линия состоит из концентрических
окружностей с центром в полюсе,
радиусы которых r
определяются по формуле
![]() ,
где n
—любое целое положительное число или
нуль. 167.
Черт. 71 и черт. 72,
,
где n
—любое целое положительное число или
нуль. 167.
Черт. 71 и черт. 72,
дачи удовлетворяют две
окружности, уравнения которых в полярных
координатах
![]() ,
,
![]() .
204.
.
204.
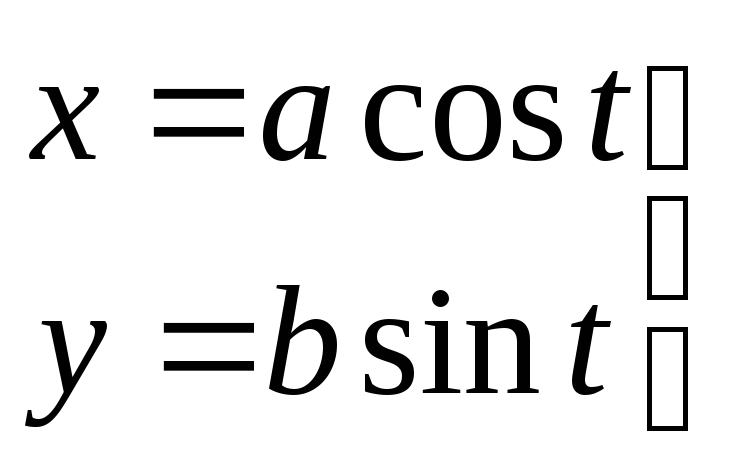 ,
,
![]() .
205.
.
205.
![]() ,
,
![]()
206.
![]() ,
,
![]()
207. 1)
![]() ,
,
![]() ;
2)
;
2)![]() ,
,
![]() ; 3)
; 3)
![]() ,
,
![]() .
208.
1)
.
208.
1)
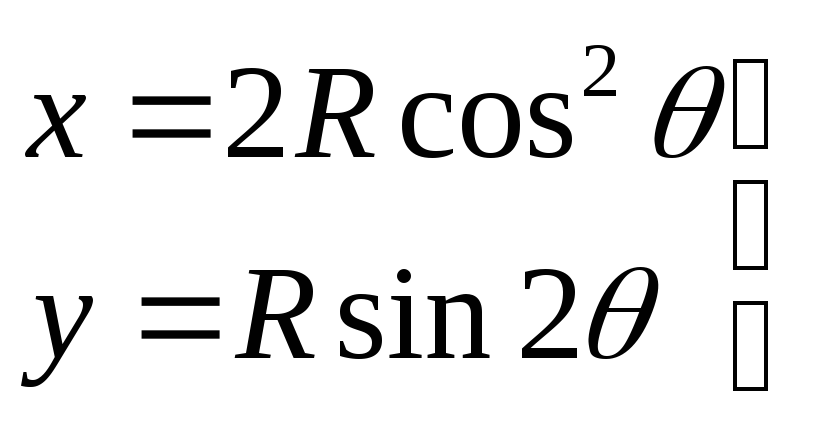 2)
2)
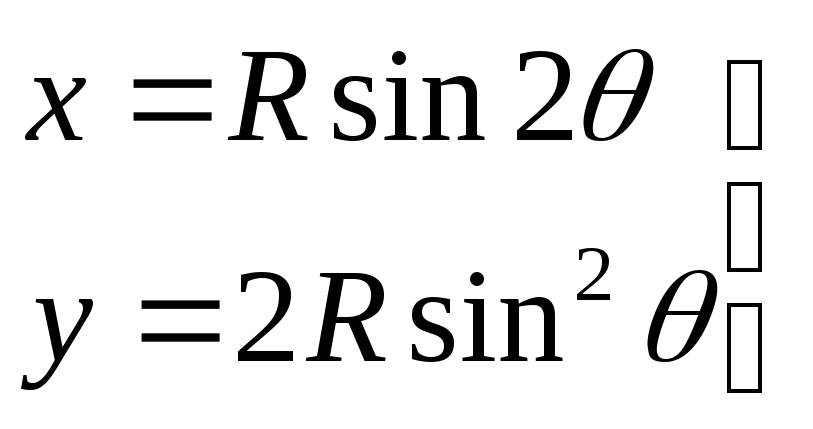 3)
3)
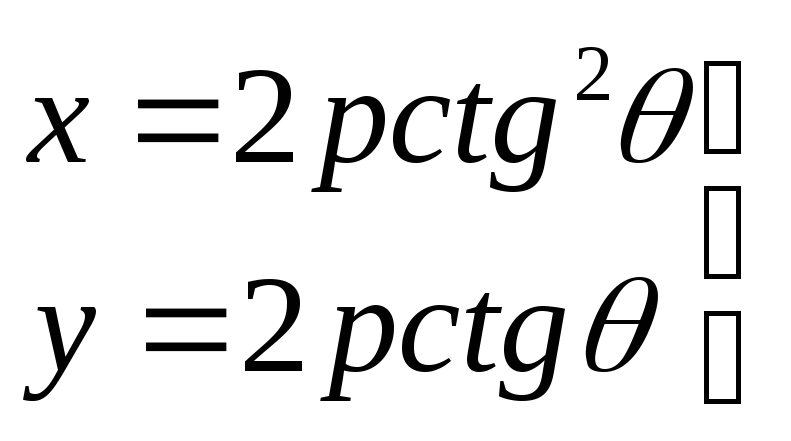 .
209.
1)
.
209.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]()