ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.07.2024
Просмотров: 373
Скачиваний: 0
СОДЕРЖАНИЕ
2. Описание лабораторного стенда и порядок выполнения работы
Измерение теплоёмкости воздуха
2. Описание лабораторного стенда
4. Обработка результатов измерения
2. Описание лабораторного стенда
4. Обработка результатов измерения
2. Описание лабораторного стенда
4. Обработка результатов измерения
1. Основные теоретические положения
2.1. Теплоотдача от горизонтальной трубы (поперечное обтекание)
Температурный коэффициент объёмного расширения:
Коэффициент кинематической вязкости:
2.2. Теплоотдача от вертикальной трубы (продольное обтекание)
Переходный режим (2320 Re 104)
2. Описание лабораторного стенда
4. Обработка результатов измерений
4. Описание лабораторного стенда
5. Контрольные вопросы
Что называется теплоёмкостью?
Какие существуют виды удельной теплоёмкости?
Что такое средняя и истинная теплоёмкость?
Что называется изобарной и изохорной теплоёмкостью? Как они взаимосвязаны?
Какая из двух теплоёмкостей больше: Cp или Cv и почему? Объяснение дать на основе 1-го закона термодинамики.
Каковы особенности практического применения формулы Майера?
Почему не существуют понятия изотермической и адиабатной теплоёмкости?

ИЗУЧЕНИЕ ПРОЦЕССА АДИАБАТНОГО
ИСТЕЧЕНИЯ ГАЗА ЧЕРЕЗ
СУЖАЮЩЕЕСЯ СОПЛО
Цель работы: экспериментальное и теоретическое исследование термодинамических характеристик процесса истечения газа из сужающегося сопла.
Задания:
1. Для заданного газа получить зависимость действительных скорости истечения и расхода от располагаемого перепада давлений до и после сопла.
2. Рассчитать теоретические значения скорости и расхода газа при адиабатном истечении и сравнить с действительными.
1. Основные положения
Термодинамическое исследование процессов движения газа по каналам имеет большое практическое значение. Основные положения теории истечения газов используются при расчетах проточной части паровых и газовых турбин, реактивных двигателей, компрессоров, пневматических приводов и многих других технических систем.
Канал переменного сечения, при прохождении через который поток газа расширяется с уменьшением давления и увеличением скорости, называется соплом. В соплах происходит преобразование потенциальной энергии давления газа в кинетическую энергию потока. Если в канале происходит увеличение давления рабочего тела и уменьшение скорости его движения, то такой канал называется диффузором. В диффузорах увеличение потенциальной энергии газа осуществляется за счёт уменьшения его кинетической энергии.
Для упрощения теоретического описания процесса истечения газа принимаются следующие допущения:
газ является идеальным;
в газе отсутствует внутреннее трение, т.е. вязкость;
в процессе истечения отсутствуют необратимые потери;
газовый поток является установившимся и стационарным, т.е. в любой точке поперечного сечения потока скорость течения w и параметры состояния газа (p, v, T) одинаковы и не меняются во времени;
течение одномерное, т.е. характеристики потока изменяются только в направлении течения потока;
отсутствует теплообмен между потоком и внешней средой, т.е. процесс истечения является адиабатным.
Теоретическое описание процесса истечения газа основано на следующих уравнениях.
Уравнение состояния идеального газа:
рv = RT, (1)
где R – газовая постоянная;
T – абсолютная температура газового потока.
Уравнение адиабаты (уравнение Пуассона):
![]() ,
(2)
,
(2)
где p – абсолютное давление газа;
k – показатель адиабаты.
Уравнение неразрывности потока:
![]() ,
(3)
,
(3)
где F – площадь поперечного сечения потока;
w – скорость потока;
v – удельный объём газа.
Уравнение Бернулли для сжимаемого рабочего тела с учетом отсутствия внутреннего трения:
![]() .
(4)
.
(4)
Это уравнение показывает, что с возрастанием давления газа его скорость и кинетическая энергия всегда уменьшаются, и наоборот, с уменьшением давления скорость и кинетическая энергия газа возрастают.
Уравнение 1-го закона термодинамики для потока.
1-й закон термодинамики в общем случае имеет следующий вид:
dq = du + dl, (5)
где dq – элементарное количество теплоты, подводимое к системе;
du – элементарное изменение внутренней энергии системы;
dl – элементарная работа изменения объёма, совершаемая системой.
В случае подвижной термодинамической системы (поток движущегося газа) часть работы изменения объёма затрачивается на преодоление сил внешнего давления, т.е. собственно на перемещение газа. Эта часть общей работы называется работой проталкивания. Оставшаяся часть работы изменения объёма может быть использована полезно, например, затрачена на вращение колеса турбины. Эта часть общей работы системы называется располагаемой (технической) работой.
Таким образом, в случае потока газа работа изменения объёма складывается из 2-х слагаемых – работы проталкивания и технической (располагаемой) работы:
![]() ,
(6)
,
(6)
где dlпр = d(pv) – элементарная работа проталкивания;
dlтехн = –vdp – элементарная техническая работа.
Тогда 1-й закон термодинамики для потока будет иметь вид:
![]() (7)
(7)
![]() ,
(8)
,
(8)
где dh – элементарное изменение энтальпии системы.
В случае адиабатного истечения
![]() .
(9)
.
(9)
Таким образом, при адиабатном истечении техническая работа совершается за счет убыли энтальпии газа.
На основе рассмотренных выше допущений для случая истечения газа из сосуда неограниченной емкости (при этом начальная скорость газа w1 = 0) получены формулы для определения теоретической скорости wт и массового расхода газа Gт в выходном сечении сопла:
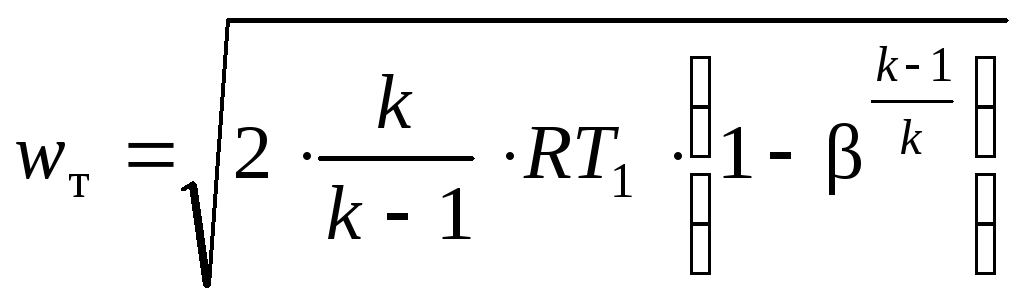 ;
(10)
;
(10)
или
![]() ;
(11)
;
(11)
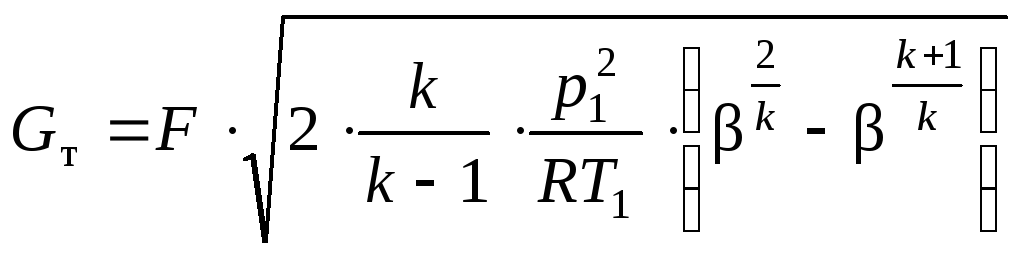 ,
(12)
,
(12)
где р1, Т1 – давление и температура газа во входном сечении сопла;
h1, h2 – удельная энтальпия потока соответственно на входе в сопло и выходе из сопла;
k – показатель адиабаты;
R – газовая постоянная;
![]() –отношение
давлений на выходе из сопла и на входе
в сопло;
–отношение
давлений на выходе из сопла и на входе
в сопло;
F – площадь выходного сечения сопла.
Анализ полученных формул показывает, что согласно принятой теории графики зависимости теоретической скорости и массового расхода от отношения давлений должны иметь вид, представленный кривыми, обозначенными буквой Т (рис. 1, 2). Из графиков следует, что при уменьшении значений от 1 до 0 скорость истечения должна непрерывно возрастать (рис. 1), а массовый расход сначала должен увеличиваться до некоторого максимального значения, а затем должен уменьшаться вплоть до 0 при = 0 (рис. 2).
W Wmax Т К кр
0,5 Д =
Р2/Р1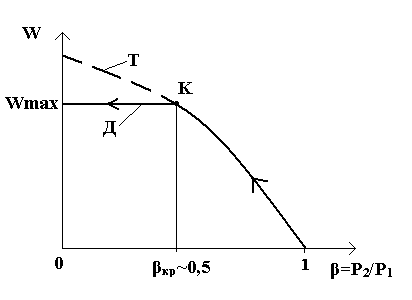
Рис. 1. Зависимость скорости истечения от отношения давлений
кр
0,5 =
Р2/Р1 Д К Т Gmax G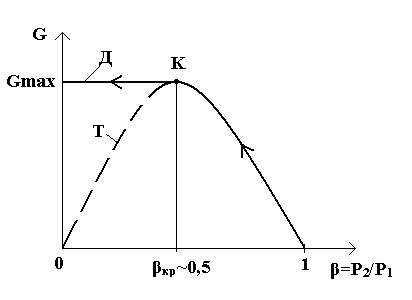
Рис. 2. Зависимость массового расхода от отношения давлений
Однако при экспериментальном исследовании истечения газов из сужающегося сопла было обнаружено, что при уменьшении от 1 до 0 действительные скорость истечения и соответственно действительный расход сначала возрастают в полном соответствии с принятой теорией процесса, но после достижения максимума своих значений при дальнейшем уменьшении вплоть до 0 остаются неизменными:
![]() .
.
Характер этих зависимостей представлен на графиках кривыми, обозначенными буквой Д (рис. 1, 2).
Физическое объяснение расхождения теоретической зависимости с экспериментальными данными было впервые предложено в 1839 г. французским ученым Сен-Венаном. Оно подтвердилось дальнейшими исследованиями. Известно, что любое, даже слабое возмущение неподвижной среды распространяется в ней со скоростью звука. В потоке, движущемся через сопло навстречу источнику возмущения, скорость передачи возмущения внутрь сопла, т.е. против направления движения потока будет ниже на величину скорости самого потока. Это так называемая относительная скорость распространения возмущения, которая равна wотн = wзв – w. При прохождении волны возмущения внутрь сопла вдоль всего потока происходит соответствующее перераспределение давлений, результатом которого согласно теории является возрастание скорости истечения и расхода газа. При постоянном давлении газа на входе в сопло P1 = const понижению давления среды, в которую вытекает газ, соответствует понижение значения β.
Однако, если давление среды, в которую вытекает газ, снизится до некоторого значения, при котором скорость истечения на выходе из сопла станет равной местной скорости звука, волна возмущения не сможет распространиться внутрь сопла, поскольку относительная скорость её распространения в среде в направлении, противоположном движению, будет равна нулю:
wотн = wзв – w = 0.
В связи с этим, перераспределения давлений в потоке вдоль сопла произойти не сможет, и скорость истечения газа на выходе из сопла останется неизменной и равной местной скорости звука. Иными словами, поток как бы «выдувает» создаваемое снаружи разрежение из сопла. Как сильно ни понижалось бы далее абсолютное давление среды за соплом, дальнейшего возрастания скорости истечения, а значит, и расхода происходить не будет, так как, согласно Рейнольдсу, «сопло перестает чувствовать, что происходит за его пределами» или, как иногда еще говорят, «сопло запирается». Некоторой аналогией этому явлению является ситуация, которую можно наблюдать порой, когда звук голоса человека сносится потоком сильного встречного ветра, и его слова собеседник не может услышать, будучи даже совсем близко, если ветер дует от него навстречу говорящему.
Режим истечения, при котором скорость истечения на выходе из сопла достигает местной скорости звука, называется критическим режимом. Скорость истечения wк, расход Gк и отношение давлений βк, соответствующие данному режиму, также называются критическими. Этому режиму соответствуют максимальные значения скорости истечения и расхода, которые могут быть достигнуты при истечении газа через обычное сужающееся сопло. Критическое отношение давлений определяется по формуле
![]() ,
(13)
,
(13)
где k – показатель адиабаты.
Критическое отношение давлений зависит только от рода газа и для конкретного газа является постоянным. Так, например:
для одноатомных газов k = 1,66 и к 0,489;
для 2-х атомных газов и воздуха k = 1,4 и к 0,528;
для 3-х и многоатомных газов k =1,3 и к 0,546.
Таким образом, теоретические зависимости для определения скорости истечения и расхода газа, полученные в рамках принятых допущений, в действительности справедливы только в области значений к ≤ β ≤ 1. При значениях β < к скорость истечения и расход в действительности остаются постоянными и максимальными для данных условий.