Файл: Программа Математическое моделирование в экономике и технике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 60
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i и соответствующих им событий Аi одинаковы: Р (Х = хi) = Р (Аi) = рi. Итак, появление в испытании события А равносильно событию, заключающемуся в том, что дискретная случайная величина Х приняла возможное значение хi.
Сформулируем правило для данного случая: для того, чтобы разыграть испытание, в котором наступает одно из событий А1, А2, …, Аn полной группы, вероятности которых соответственно равны р1, р2, …, рn, достаточно разыграть дискретную случайную величину Х с законом распределения:
Если в испытании величина Х приняла возможное значение хi=i, то наступило событие Аi.
Пример 3. Пусть заданы вероятности четырех событий, образующих полную группу: р1=Р(А1)=0,19, р2=Р(А2)=0,21, р3=Р(А3)=0,34, р4=Р(А4)=0,26. Нужно разыграть пять испытаний, в каждом из которых появляется одно из четырех заданных событий.
Решение.
В соответствии с приведенном выше правилом, нужно разыграть дискретную случайную величину Х, закон распределения которой:
Разобьем интервал (0, 1) на четыре интервала: ∆1=(0; 0,19), ∆2=(0,19; 0,40), ∆3=(0,40; 0,74), ∆4=(0,74; 1). Выберем из таблицы 5 случайных чисел: 0,66; 0,31; 0,85; 0,63; 0,73. Случайное число r1=0,66 принадлежит интервалу ∆3, поэтому Х=3 и, следовательно, наступило событие А3. Аналогично были найдены остальные события. В результате получается следующая последовательность событий: А3, А2, А4, А3, А3.
Пример 4. События А и В независимы и совместны. Нужно разыграть 6 испытаний, в каждом из которых вероятность появления события А равна 0,6, а вероятность появления события В равна 0,2.
Решение.
Необходимо рассмотреть 4 возможных исхода испытания:
А1=АВ, причем в силу независимости событий Р(АВ)=Р(А)·Р(В)=0,6·0,2=0,12.
А2=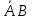
, причем Р(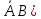 =0,4·0,2=0,08.
=0,4·0,2=0,08.
А3=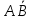 , причем Р(
, причем Р(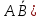 =0,6·0,8=0,48.
=0,6·0,8=0,48.
А4=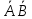 , причем Р(
, причем Р(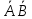 )=0,4·0,8=0,32.
)=0,4·0,8=0,32.
Таким образом, задача сводится к разыгрыванию полной группы четырех событий: А1 с вероятностью р1=0,12, А2 с вероятностью р2=0.08, А3 с вероятностью р3=0,48, А4 с вероятностью р4=0,32.
Далее, данная задача сводится к разыгрыванию дискретной случайной величины Х с законом распределения:
Выберем 6 чисел из таблицы случайных величин: 0,45; 0,65; 0,06; 0,59; 0,33; 0,70. Разобьем интервал (0, 1) на следующие интервалы: ∆1=(0; 0,12), ∆2=(0,12; 0,20), ∆3=(0,20; 0,68), ∆4=(0,68; 1). Случайное число r1=0,45 принадлежит интервалу ∆3, и, следовательно, наступило событие А3. Аналогично найдем исходы остальных испытаний.
Получаем следующую последовательность исходов разыгранных испытаний: А3, А3, А1, А3, А3, А4 или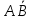 ,
,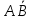 , АВ,
, АВ, 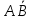 ,
, 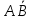 ,
, 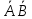 .
.
Пример 5. События А и В зависимы и совместны. Необходимо разыграть 4 испытания, в каждом из которых заданы вероятности Р(А)=0,6; Р(В)=0,6; Р(АВ)=0,5.
Решение.
Необходимо рассмотреть 4 исходы испытания:
А1=АВ, причем, по условию, Р(АВ)=0,5;
А2=А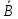 , причем Р(А
, причем Р(А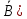 =Р(А) - Р(АВ)=0,8-0,5=0,3;
=Р(А) - Р(АВ)=0,8-0,5=0,3;
А3= , причем Р(
, причем Р( )=Р(В)-Р(АВ)=0,6-0,5=0,1;
)=Р(В)-Р(АВ)=0,6-0,5=0,1;
А4= , причем Р(
, причем Р( )=1 – (Р(А1)+Р(А2)+Р(А3))=1-(0,5+0,3+0,1)=0,1.
)=1 – (Р(А1)+Р(А2)+Р(А3))=1-(0,5+0,3+0,1)=0,1.
Таким образом, задача сводится к разыгрыванию полной группы четырех событий: А1 с вероятностью 0,5, А2 с вероятностью 0,3, А3 с вероятностью 0,1 и А4 с вероятностью 0,1.
Далее, эта задача сводится к разыгрыванию дискретной случайной величины Х с законом распределения:
Выберем 4 числа из таблицы случайных чисел: 0,65; 0,06; 0,59; 0,33. Разобьем интервал (0, 1) на следующие интервалы: ∆1=(0; 0,5), ∆2=(0,5; 0,8), ∆3=(0,8; 0,9), ∆4=(0,9; 1). Случайное число r1=0,65 принадлежит интервалу ∆2, и, следовательно, наступило событие А2. Аналогично найдем исходы остальных испытаний.
В результате получим следующую последовательность исходов разыгранных испытаний: А2, А1, А2, А1 или А , АВ, А
, АВ, А , АВ.
, АВ.
Метод обратных функций.
Пусть требуется разыграть непрерывную случайную величину Х, т.е. нужно получить последовательность ее возможных значений хi (i=1,2,…), зная функцию распределения F(x).
Теорема 1. Если rj – случайное число, то возможное значение xi разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F(x), соответствующее rj является корней уравнения
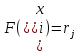 (*)
(*)
Докажем это утверждение.
Доказательство. Выберем случайное число rj (0 ≤ rj < 1). В силу того, что в интервале возможных значений Х функция F(x) монотонно возрастает от 0 до 1, в этом интервале существует, причем единственное, значение аргумента xi, при котором функция распределения примет значения rj. Иными словами, для уравнения (*) существует единственное решение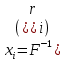
, где F-1 – функция, обратная к функции F(x).
Теперь докажем, что корень xi уравнения (*) и есть возможное значение непрерывной случайной величины (обозначим ее за ξ, а позже убедимся в том, что ξ=Х). Для этого докажем, что вероятность попадание ξ в интервал (a,b), принадлежащий интервалу всех возможных значений Х, равна приращению функции распределения F(x) на этой интервале: Р(a< ξ
В силу того, что F(x) – монотонно возрастающая функция в интервале всех возможных значений Х, то в этом интервале большему значению аргумента соответствует большее значение функции, и наоборот. Из этого следует, что если aij
Из приведенных выше неравенств следует: a < ξ < b, (**)
F(a)
Таким образом, неравенства (**) и (***) равносильны, а, значит, и равновероятны:
P(a< ξ
Поскольку величина R распределена равномерно в интервале (0,1), то вероятность попадания R в некоторый интервал, принадлежащий интервалу (0,1), равна его длине. В частности,
P(F(a)
Из этого следует, что соотношение (****) можно записать в виде
P(a< ξ
Таким образом, вероятность попадания ξ в интервал (a,b) равна приращению функции распределения F(x) на этом интервале, а это означает, что ξ=Х. Иными словами, числа xi, которые определяются формулой (*), есть возможные значения величины Х с заданной функцией распределения F(x).
Правило. Для того, чтобы найти возможное значение хi непрерывной случайной величины Х, зная ее функцию распределения, нужно выбрать случайное число rj, приравнять его к функции распределения, решить относительно xi полученное уравнение: F(xi)=rj.
Замечание 1. Если решить уравнение в явном виде не удается, то можно прибегнуть к графическим или численным методам.
Пример 6. Разыграть 3 возможных значения непрерывной случайной величины Х, распределенной равномерно в интервале (2;10).
Решение.
Выпишем функцию распределения величины Х, которая распределена равномерно на интервале (a,b):
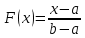 .
.
Из условия, a=2, b=10, поэтому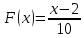 .
.
В силу правила, записанного выше, запишем уравнение для отыскания возможных значение xi, т.е. приравняем функцию распределения случайному числу: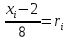 ⇒ хi=8ri+2.
⇒ хi=8ri+2.
Из таблицы случайных чисел выберем 3 числа: 0,11; 0,17; 0,66. Подставив эти числа в уравнение, получим возможные значения Х:
х1 = 8·0,11+2 = 2,88
х2 = 8·0,17+2 = 3,36
х3 = 8·0,66+2 = 7,28
Пример 7. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения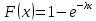 , (x > 0).
, (x > 0).
Необходимо найти явную формулу для разыгрывания возможных значений Х.
Решение.
С использованием правила, запишем уравнение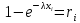 .
.
Решим уравнение относительно хi.
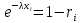 ⇒
⇒ 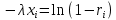 ⇒
⇒ 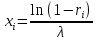 .
.
Случайное число ri заключено в интервале (0;1); следовательно, число 1 – ri, также случайное и принадлежит интервалу (0,1). Иными словами, величины R и 1 – R распределены одинаково. Поэтому, для отыскания xi можно использовать более простую формулу: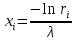 .
.
Замечание 2. Известно, что
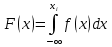 .
.
В частности,
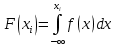 .
.
Отсюда следует, что если известна плотность вероятности f(x), то для разыгрывания Х можно вместо уравнения F(xi)=ri решить относительно хi решить уравнение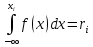 .
.
Правило. Для того, чтобы найти возможное значение хi непрерывной случайной величины Х, зная ее плотность вероятности f(x) надо выбрать случайное число ri и решить относительно xi уравнение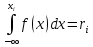 или уравнение
или уравнение 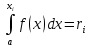 , где а – наименьшее конечное возможное значение Х.
, где а – наименьшее конечное возможное значение Х.
Пример 8. Пусть задана плотность вероятности непрерывной случайной величины Х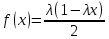 в интервале (0;
в интервале (0; 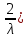 ; вне это интервала f(x)=0. Нужно найти явную формулу для разыгрывания возможных значений Х.
; вне это интервала f(x)=0. Нужно найти явную формулу для разыгрывания возможных значений Х.
Решение.
С использованием указанного выше правила запишем уравнение:
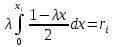 .
.
Выполнив интегрирование и решив полученное квадратное уравнение относительно xi, получим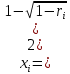 .
.
Функция распределения разыгрываемой случайной величины Х может быть представлена в виде линейной комбинации двух функций распределения: F(x) = C1F1(x) + C2F2(x), (C1>0, C2>0).
При х→∞ каждая функция распределения будет стремится к 1 ⇒ С1+С2=1.
Введем вспомогательную дискретную случайную величину Z с законом распределения
Не трудно заметить, что P(Z=1)=C1, P(Z=2)=C2 (*)
Возьмем два независимых случайных числа r1 и r2. По числу r1 разыгрываем возможное значение Z. Если окажется, что Z=1, то ищут искомое возможное значение Х из уравнения F1(x)=r2, если Z=2, то решают относительно х уравнение F2(x)=r2.
Докажем, что функция распределения разыгрываемой случайной величины равна заданной функции распределения. Для этого воспользуемся формулой полной вероятности P(A)=P(B1)PB1(A)+P(B2)PB2(A).
Обозначим через А событие Х<х ⇒ P(A)=P(X<x)=F(x). (**)
Рассмотрим гипотезы В1: Z=1 и В2: Z=2.
Из (*) ⇒ Р(В1)=Р(Z=1)=C1 и P(B2)=P(Z=2)=C2. (***)
Условные вероятности появления события А соответственно равны:
РВ1(А)=РВ1(Х<х)=F1(x) и PB2(A)=PB2(X<x)=F2(x) (****)
Подставим (**), (***), (****) в формулу полной вероятности:
F(x)=C1F1(x)+C2F2(x).
Замечание. Метод суперпозиции можно обобщить для n слагаемых функции распределения.
Правило. Для того, чтобы разыграть возможное значение случайной величины Х, функция распределения которой F(x)=C1F1(x)+C2F2(x), где С1>0, С2>0, С1+С2=1, нужно выбрать два независимых случайных числа r1 и r2 и по случайному числу r1 разыграть возможное значение вспомогательной дискретной случайной величины Z с законом распределения
Если окажется, что Z=1, то решается уравнение F1(x)=r2 относительно х, если Z=2, то решается уравнение F2(x)=r2.
Пример 9. Нужно найти явные формулы для разыгрывания непрерывной случайной величины Х, заданной функцией распределения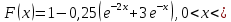 ∞.
∞.
Решение.
Применим метод суперпозиции, для этого заданную функцию перепишем в виде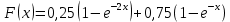 .
.
Получим: F1(x) =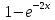 ; F2(x) =
; F2(x) = 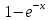 ; C1 = 0,25; C2 = 0,75.
; C1 = 0,25; C2 = 0,75.
Введем вспомогательную дискретную случайную величину Z с законом распределения
Выберем независимые случайные числа r1 и r2. Разыграем Z по случайному числу r1. Для этого разобьем интервал (0,1) на частичные интервалы ∆1=(0;0,25), ∆2=(0,25;1). Если r1<0,25, то Z=1, если r1≥0,25, то Z=2.
Возможное значение Х находят, решая уравнение относительно х:
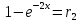 или
или 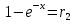 .
.
Используя решение примера 7, в котором была найдена явная формула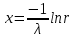 для разыгрывания возможных значений показательного распределения с заданным параметром λ. В результате получим:
для разыгрывания возможных значений показательного распределения с заданным параметром λ. В результате получим:
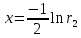 , если r1<0,25;
, если r1<0,25;
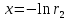 , если r1≥0,25.
, если r1≥0,25.
Прежде чем перейти к рассмотрению вопроса о приближенном разыгрывание нормальной случайной величины, вспомним следующее: если случайная величина R равномерно распределена на интервале (0,1), то ее математическое ожидание и дисперсия равны:
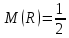 , (*)
, (*)
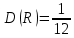 . (**)
. (**)
Составим сумму n независимых и распределенных равномерно на интервале (0,1) случайных величин Rj (j=1, 2,…, n):
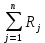 . (***)
. (***)
Для того, чтобы нормировать эту сумму, найден предварительно ее математическое ожидание и дисперсию.
Поскольку математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых, а сумма содержит n слагаемых, каждое из которых равно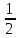 , получим:
, получим:
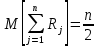 .
.
Поскольку дисперсия суммы случайных величин равно сумме дисперсий слагаемых, а сумма содержит n слагаемых, каждое из которых равно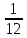 , получим:
, получим:
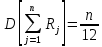 .
.
Тогда, среднее квадратическое отклонение суммы (***) равно:
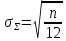 .
.
Пронормируем рассматриваемую сумму. Для этого вычтем математическое ожидание и разделим результат на среднее квадратическое отклонение:
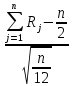 .
.
При n→∞ распределение этой нормированной случайной величины стреметися к нормальному с параметрами а=0 и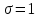 . При конечном числе n распределение приближенно нормальное. В частности, если n=12 получим удобное для расчета приближение:
. При конечном числе n распределение приближенно нормальное. В частности, если n=12 получим удобное для расчета приближение: 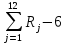 .
.
Правило. Для того, чтобы разыграть возможное значение хi нормальной случайной величины Х с параметрами а=0 и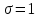 , нужно сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:
, нужно сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:
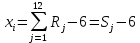 .
.
Пример 10. а) Разыграть 100 возможных значений нормальной величины Х с параметрами а=0 и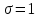 ;
;
б) Оценить параметры разыгранной величины.
Решение.
а) Выберем 12 случайных чисел из первой строки таблицы случайных чисел, сложим их и из полученной суммы вычтем 6.
В результате получим: xi=(0,10 + 0,09 +…+ 0,67) – 6 = - 0,99.
Аналогично, выбирая из каждой следующей строки таблицы первые 12 чисел, найден остальные возможные значения Х.
б) Выполнив расчеты, получим искомые оценки:
а* ≈-0,05,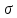 ≈1,04.
≈1,04.
Оценки удовлетворительные, поскольку а* близко к 0,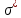 близко к 1.
близко к 1.
В ходе работы нами была изучены способы разыгрывания случайных величин. Нами отдельно были рассмотрены разыгрывание дискретной случайной величины, разыгрывание противоположных событий, разыгрывание полной группы событий, разыгрывание непрерывной случайной величины, а также метод суперпозиций и приближенное разыгрывание нормальной случайной величины.
Кроме того, мы выяснили, что случайных величины имеют чрезвычайно важное значение при решении задач из различных сфер человеческой деятельности. С помощью разыгрывания случайных величин решают задачи различной сложности и назначения. В настоящий момент случайные величины находят очень широкое применение в различных областях науки, техники, социальных аспектах, поэтому исследования в данной области продолжаются.

Сформулируем правило для данного случая: для того, чтобы разыграть испытание, в котором наступает одно из событий А1, А2, …, Аn полной группы, вероятности которых соответственно равны р1, р2, …, рn, достаточно разыграть дискретную случайную величину Х с законом распределения:
| X | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Если в испытании величина Х приняла возможное значение хi=i, то наступило событие Аi.
Пример 3. Пусть заданы вероятности четырех событий, образующих полную группу: р1=Р(А1)=0,19, р2=Р(А2)=0,21, р3=Р(А3)=0,34, р4=Р(А4)=0,26. Нужно разыграть пять испытаний, в каждом из которых появляется одно из четырех заданных событий.
Решение.
В соответствии с приведенном выше правилом, нужно разыграть дискретную случайную величину Х, закон распределения которой:
| X | 1 | 2 | 3 | 4 |
| p | 0,19 | 0,21 | 0,34 | 0,26 |
Разобьем интервал (0, 1) на четыре интервала: ∆1=(0; 0,19), ∆2=(0,19; 0,40), ∆3=(0,40; 0,74), ∆4=(0,74; 1). Выберем из таблицы 5 случайных чисел: 0,66; 0,31; 0,85; 0,63; 0,73. Случайное число r1=0,66 принадлежит интервалу ∆3, поэтому Х=3 и, следовательно, наступило событие А3. Аналогично были найдены остальные события. В результате получается следующая последовательность событий: А3, А2, А4, А3, А3.
Пример 4. События А и В независимы и совместны. Нужно разыграть 6 испытаний, в каждом из которых вероятность появления события А равна 0,6, а вероятность появления события В равна 0,2.
Решение.
Необходимо рассмотреть 4 возможных исхода испытания:
А1=АВ, причем в силу независимости событий Р(АВ)=Р(А)·Р(В)=0,6·0,2=0,12.
А2=
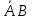
, причем Р(
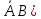 =0,4·0,2=0,08.
=0,4·0,2=0,08.А3=
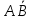 , причем Р(
, причем Р(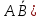 =0,6·0,8=0,48.
=0,6·0,8=0,48.А4=
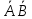 , причем Р(
, причем Р(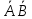 )=0,4·0,8=0,32.
)=0,4·0,8=0,32.Таким образом, задача сводится к разыгрыванию полной группы четырех событий: А1 с вероятностью р1=0,12, А2 с вероятностью р2=0.08, А3 с вероятностью р3=0,48, А4 с вероятностью р4=0,32.
Далее, данная задача сводится к разыгрыванию дискретной случайной величины Х с законом распределения:
| Х | 1 | 2 | 3 | 4 |
| р | 0,12 | 0,08 | 0,48 | 0,32 |
Выберем 6 чисел из таблицы случайных величин: 0,45; 0,65; 0,06; 0,59; 0,33; 0,70. Разобьем интервал (0, 1) на следующие интервалы: ∆1=(0; 0,12), ∆2=(0,12; 0,20), ∆3=(0,20; 0,68), ∆4=(0,68; 1). Случайное число r1=0,45 принадлежит интервалу ∆3, и, следовательно, наступило событие А3. Аналогично найдем исходы остальных испытаний.
Получаем следующую последовательность исходов разыгранных испытаний: А3, А3, А1, А3, А3, А4 или
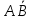 ,
,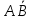 , АВ,
, АВ, 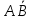 ,
, 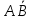 ,
, 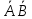 .
.Пример 5. События А и В зависимы и совместны. Необходимо разыграть 4 испытания, в каждом из которых заданы вероятности Р(А)=0,6; Р(В)=0,6; Р(АВ)=0,5.
Решение.
Необходимо рассмотреть 4 исходы испытания:
А1=АВ, причем, по условию, Р(АВ)=0,5;
А2=А
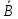 , причем Р(А
, причем Р(А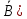 =Р(А) - Р(АВ)=0,8-0,5=0,3;
=Р(А) - Р(АВ)=0,8-0,5=0,3;А3=
 , причем Р(
, причем Р( )=Р(В)-Р(АВ)=0,6-0,5=0,1;
)=Р(В)-Р(АВ)=0,6-0,5=0,1;
А4=
 , причем Р(
, причем Р( )=1 – (Р(А1)+Р(А2)+Р(А3))=1-(0,5+0,3+0,1)=0,1.
)=1 – (Р(А1)+Р(А2)+Р(А3))=1-(0,5+0,3+0,1)=0,1.Таким образом, задача сводится к разыгрыванию полной группы четырех событий: А1 с вероятностью 0,5, А2 с вероятностью 0,3, А3 с вероятностью 0,1 и А4 с вероятностью 0,1.
Далее, эта задача сводится к разыгрыванию дискретной случайной величины Х с законом распределения:
| Х | 1 | 2 | 3 | 4 |
| р | 0,5 | 0,3 | 0,1 | 0,1 |
Выберем 4 числа из таблицы случайных чисел: 0,65; 0,06; 0,59; 0,33. Разобьем интервал (0, 1) на следующие интервалы: ∆1=(0; 0,5), ∆2=(0,5; 0,8), ∆3=(0,8; 0,9), ∆4=(0,9; 1). Случайное число r1=0,65 принадлежит интервалу ∆2, и, следовательно, наступило событие А2. Аналогично найдем исходы остальных испытаний.
В результате получим следующую последовательность исходов разыгранных испытаний: А2, А1, А2, А1 или А
 , АВ, А
, АВ, А , АВ.
, АВ.-
Разыгрывание непрерывной случайной величины
Метод обратных функций.
Пусть требуется разыграть непрерывную случайную величину Х, т.е. нужно получить последовательность ее возможных значений хi (i=1,2,…), зная функцию распределения F(x).
Теорема 1. Если rj – случайное число, то возможное значение xi разыгрываемой непрерывной случайной величины Х с заданной функцией распределения F(x), соответствующее rj является корней уравнения
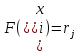 (*)
(*)Докажем это утверждение.
Доказательство. Выберем случайное число rj (0 ≤ rj < 1). В силу того, что в интервале возможных значений Х функция F(x) монотонно возрастает от 0 до 1, в этом интервале существует, причем единственное, значение аргумента xi, при котором функция распределения примет значения rj. Иными словами, для уравнения (*) существует единственное решение
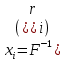
, где F-1 – функция, обратная к функции F(x).
Теперь докажем, что корень xi уравнения (*) и есть возможное значение непрерывной случайной величины (обозначим ее за ξ, а позже убедимся в том, что ξ=Х). Для этого докажем, что вероятность попадание ξ в интервал (a,b), принадлежащий интервалу всех возможных значений Х, равна приращению функции распределения F(x) на этой интервале: Р(a< ξ
В силу того, что F(x) – монотонно возрастающая функция в интервале всех возможных значений Х, то в этом интервале большему значению аргумента соответствует большее значение функции, и наоборот. Из этого следует, что если a
Из приведенных выше неравенств следует: a < ξ < b, (**)
F(a)
Таким образом, неравенства (**) и (***) равносильны, а, значит, и равновероятны:
P(a< ξ
Поскольку величина R распределена равномерно в интервале (0,1), то вероятность попадания R в некоторый интервал, принадлежащий интервалу (0,1), равна его длине. В частности,
P(F(a)
Из этого следует, что соотношение (****) можно записать в виде
P(a< ξ
Таким образом, вероятность попадания ξ в интервал (a,b) равна приращению функции распределения F(x) на этом интервале, а это означает, что ξ=Х. Иными словами, числа xi, которые определяются формулой (*), есть возможные значения величины Х с заданной функцией распределения F(x).
Правило. Для того, чтобы найти возможное значение хi непрерывной случайной величины Х, зная ее функцию распределения, нужно выбрать случайное число rj, приравнять его к функции распределения, решить относительно xi полученное уравнение: F(xi)=rj.
Замечание 1. Если решить уравнение в явном виде не удается, то можно прибегнуть к графическим или численным методам.
Пример 6. Разыграть 3 возможных значения непрерывной случайной величины Х, распределенной равномерно в интервале (2;10).
Решение.
Выпишем функцию распределения величины Х, которая распределена равномерно на интервале (a,b):
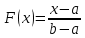 .
.Из условия, a=2, b=10, поэтому
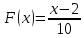 .
.В силу правила, записанного выше, запишем уравнение для отыскания возможных значение xi, т.е. приравняем функцию распределения случайному числу:
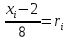 ⇒ хi=8ri+2.
⇒ хi=8ri+2.Из таблицы случайных чисел выберем 3 числа: 0,11; 0,17; 0,66. Подставив эти числа в уравнение, получим возможные значения Х:
х1 = 8·0,11+2 = 2,88
х2 = 8·0,17+2 = 3,36
х3 = 8·0,66+2 = 7,28
Пример 7. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения
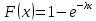 , (x > 0).
, (x > 0).Необходимо найти явную формулу для разыгрывания возможных значений Х.
Решение.
С использованием правила, запишем уравнение
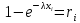 .
.Решим уравнение относительно хi.
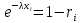 ⇒
⇒ 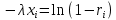 ⇒
⇒ 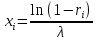 .
.Случайное число ri заключено в интервале (0;1); следовательно, число 1 – ri, также случайное и принадлежит интервалу (0,1). Иными словами, величины R и 1 – R распределены одинаково. Поэтому, для отыскания xi можно использовать более простую формулу:
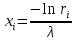 .
.Замечание 2. Известно, что
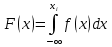 .
.В частности,
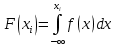 .
.Отсюда следует, что если известна плотность вероятности f(x), то для разыгрывания Х можно вместо уравнения F(xi)=ri решить относительно хi решить уравнение
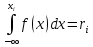 .
.Правило. Для того, чтобы найти возможное значение хi непрерывной случайной величины Х, зная ее плотность вероятности f(x) надо выбрать случайное число ri и решить относительно xi уравнение
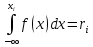 или уравнение
или уравнение 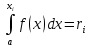 , где а – наименьшее конечное возможное значение Х.
, где а – наименьшее конечное возможное значение Х.Пример 8. Пусть задана плотность вероятности непрерывной случайной величины Х
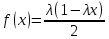 в интервале (0;
в интервале (0; 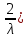 ; вне это интервала f(x)=0. Нужно найти явную формулу для разыгрывания возможных значений Х.
; вне это интервала f(x)=0. Нужно найти явную формулу для разыгрывания возможных значений Х.Решение.
С использованием указанного выше правила запишем уравнение:
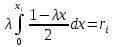 .
.Выполнив интегрирование и решив полученное квадратное уравнение относительно xi, получим
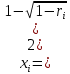 .
.-
Метод суперпозиций
Функция распределения разыгрываемой случайной величины Х может быть представлена в виде линейной комбинации двух функций распределения: F(x) = C1F1(x) + C2F2(x), (C1>0, C2>0).
При х→∞ каждая функция распределения будет стремится к 1 ⇒ С1+С2=1.
Введем вспомогательную дискретную случайную величину Z с законом распределения
| Z | 1 | 2 |
| p | C1 | C2 |
Не трудно заметить, что P(Z=1)=C1, P(Z=2)=C2 (*)
Возьмем два независимых случайных числа r1 и r2. По числу r1 разыгрываем возможное значение Z. Если окажется, что Z=1, то ищут искомое возможное значение Х из уравнения F1(x)=r2, если Z=2, то решают относительно х уравнение F2(x)=r2.
Докажем, что функция распределения разыгрываемой случайной величины равна заданной функции распределения. Для этого воспользуемся формулой полной вероятности P(A)=P(B1)PB1(A)+P(B2)PB2(A).
Обозначим через А событие Х<х ⇒ P(A)=P(X<x)=F(x). (**)
Рассмотрим гипотезы В1: Z=1 и В2: Z=2.
Из (*) ⇒ Р(В1)=Р(Z=1)=C1 и P(B2)=P(Z=2)=C2. (***)
Условные вероятности появления события А соответственно равны:
РВ1(А)=РВ1(Х<х)=F1(x) и PB2(A)=PB2(X<x)=F2(x) (****)
Подставим (**), (***), (****) в формулу полной вероятности:
F(x)=C1F1(x)+C2F2(x).
Замечание. Метод суперпозиции можно обобщить для n слагаемых функции распределения.
Правило. Для того, чтобы разыграть возможное значение случайной величины Х, функция распределения которой F(x)=C1F1(x)+C2F2(x), где С1>0, С2>0, С1+С2=1, нужно выбрать два независимых случайных числа r1 и r2 и по случайному числу r1 разыграть возможное значение вспомогательной дискретной случайной величины Z с законом распределения
| Z | 1 | 2 |
| p | C1 | C2 |
Если окажется, что Z=1, то решается уравнение F1(x)=r2 относительно х, если Z=2, то решается уравнение F2(x)=r2.
Пример 9. Нужно найти явные формулы для разыгрывания непрерывной случайной величины Х, заданной функцией распределения
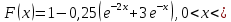 ∞.
∞.Решение.
Применим метод суперпозиции, для этого заданную функцию перепишем в виде
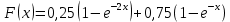 .
. Получим: F1(x) =
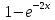 ; F2(x) =
; F2(x) = 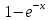 ; C1 = 0,25; C2 = 0,75.
; C1 = 0,25; C2 = 0,75.Введем вспомогательную дискретную случайную величину Z с законом распределения
| Z | 1 | 2 |
| p | 0,25 | 0,75 |
Выберем независимые случайные числа r1 и r2. Разыграем Z по случайному числу r1. Для этого разобьем интервал (0,1) на частичные интервалы ∆1=(0;0,25), ∆2=(0,25;1). Если r1<0,25, то Z=1, если r1≥0,25, то Z=2.
Возможное значение Х находят, решая уравнение относительно х:
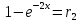 или
или 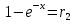 .
.Используя решение примера 7, в котором была найдена явная формула
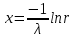 для разыгрывания возможных значений показательного распределения с заданным параметром λ. В результате получим:
для разыгрывания возможных значений показательного распределения с заданным параметром λ. В результате получим: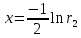 , если r1<0,25;
, если r1<0,25;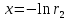 , если r1≥0,25.
, если r1≥0,25.-
Приближенное разыгрывание нормальной случайной величины
Прежде чем перейти к рассмотрению вопроса о приближенном разыгрывание нормальной случайной величины, вспомним следующее: если случайная величина R равномерно распределена на интервале (0,1), то ее математическое ожидание и дисперсия равны:
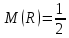 , (*)
, (*)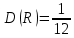 . (**)
. (**)Составим сумму n независимых и распределенных равномерно на интервале (0,1) случайных величин Rj (j=1, 2,…, n):
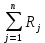 . (***)
. (***)Для того, чтобы нормировать эту сумму, найден предварительно ее математическое ожидание и дисперсию.
Поскольку математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых, а сумма содержит n слагаемых, каждое из которых равно
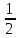 , получим:
, получим: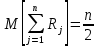 .
.Поскольку дисперсия суммы случайных величин равно сумме дисперсий слагаемых, а сумма содержит n слагаемых, каждое из которых равно
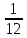 , получим:
, получим: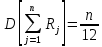 .
.Тогда, среднее квадратическое отклонение суммы (***) равно:
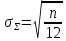 .
.Пронормируем рассматриваемую сумму. Для этого вычтем математическое ожидание и разделим результат на среднее квадратическое отклонение:
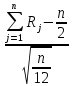 .
.При n→∞ распределение этой нормированной случайной величины стреметися к нормальному с параметрами а=0 и
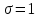 . При конечном числе n распределение приближенно нормальное. В частности, если n=12 получим удобное для расчета приближение:
. При конечном числе n распределение приближенно нормальное. В частности, если n=12 получим удобное для расчета приближение: 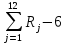 .
.Правило. Для того, чтобы разыграть возможное значение хi нормальной случайной величины Х с параметрами а=0 и
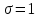 , нужно сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:
, нужно сложить 12 независимых случайных чисел и из полученной суммы вычесть 6: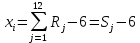 .
.Пример 10. а) Разыграть 100 возможных значений нормальной величины Х с параметрами а=0 и
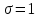 ;
;б) Оценить параметры разыгранной величины.
Решение.
а) Выберем 12 случайных чисел из первой строки таблицы случайных чисел, сложим их и из полученной суммы вычтем 6.
В результате получим: xi=(0,10 + 0,09 +…+ 0,67) – 6 = - 0,99.
Аналогично, выбирая из каждой следующей строки таблицы первые 12 чисел, найден остальные возможные значения Х.
б) Выполнив расчеты, получим искомые оценки:
а* ≈-0,05,
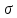 ≈1,04.
≈1,04.Оценки удовлетворительные, поскольку а* близко к 0,
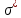 близко к 1.
близко к 1.Заключение
В ходе работы нами была изучены способы разыгрывания случайных величин. Нами отдельно были рассмотрены разыгрывание дискретной случайной величины, разыгрывание противоположных событий, разыгрывание полной группы событий, разыгрывание непрерывной случайной величины, а также метод суперпозиций и приближенное разыгрывание нормальной случайной величины.
Кроме того, мы выяснили, что случайных величины имеют чрезвычайно важное значение при решении задач из различных сфер человеческой деятельности. С помощью разыгрывания случайных величин решают задачи различной сложности и назначения. В настоящий момент случайные величины находят очень широкое применение в различных областях науки, техники, социальных аспектах, поэтому исследования в данной области продолжаются.
Список использованной литературы
-
Андронов А.М. Теория вероятностей и математическая статистика, Питер, 2004 -
Волковец А.И. Теория вероятностей и математическая статистика, конспект лекций, М.: Инфра-М,2003 -
Гмурман В.Е. Теория вероятностей и математическая статистика, М.: АСТ, 2003 -
Колемаев В.А. Теория вероятностей и математическая статистика, М.: Инфра-М, 1997 -
Ларин А.А. Теория вероятностей и математическая статистика, М.: ЭФ НГУ, 2003 -
Письменный Д. М. Конспект лекций по теории вероятностей и математической статистике, М.: Академия, 2004 -
Топчий В.А., Дворкин П.Л. Теория вероятности, ОФИМ СО РАН, 1999 -
Чернова Н.И. Теория вероятностей: курс лекций, Новосибирск: НГУ, 2006 -
Соколов Г.А., Чистякова Н.А. Теория вероятностей, Экзамен, 2005 -
Нахман А.Д. Ряды. Теория вероятностей и математическая статистика, Тамбов: ТГТУ, 2002 -
Пучков Н.П., Ткач Л.И. Математика случайного. Методические рекомендации, Тамбов: ТГТУ, 2005 -
Соловьев А.А. Лекции по теории вероятностей и математической статистике, ЧелГУ, 2003 -
Розанов Ю.А. Теория вероятностей, случайные процессы и математическая статистика, М.: Наука, 1989 -
Прохоров А.В. Задачи по теории вероятностей, М.: Наука,1986
Приложение

