Файл: Программа Математическое моделирование в экономике и технике.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТФакультет вычислительной техникиКафедра «Высшей и прикладной математики»Направление подготовки 01.04.02 «Прикладная математика и информатика» Магистерская программа «Математическое моделирование в экономике и технике»ОТЧЕТ ПО НАУЧНО-
ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЕ Выполнил: студент группы 22ВГм2Дружаева А.И,Научный руководитель: к.ф.-м.н., доцент Бойкова А. И.Работа защищена с оценкой ___________Дата защиты _________________Пенза, 2023

Оглавление

Введение

В настоящее время случайные величины с заданным законом распределения находят применение в науке, технике и в любой другой области человеческой деятельности. Поиски случайной величины с заданным законом распределения решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы случайной величин. Постановка задачи случайной величин предполагает существование конкурирующих свойств процесса.Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и на первый взгляд беспорядочно. Так, при бросании игральной кости (кубик с нумерованными гранями) может выпасть любое число от 1 до 6. Радиоактивное ядро может распасться в любую наперед избранную секунду, время жизни ядра до распада - случайная величина. Таким образом, те или иные параметры для совокупности таких изделий также являются случайными величинами. Результат каждого отдельного измерения случайной величины непредсказуем. Но при многократном повторении измерений в неизменных условиях совокупность их результатов описывается статистическими закономерностями. Если бросать игральную кость сотни раз, каждое определенное число (например, два) выпадает примерно в 1/6 части общего числа попыток; для радиоактивного вещества, содержащего очень большое число одинаковых ядер, можно надежно предсказать число распадов за любой (но не слишком малый) наперед заданный промежуток времени.

---

Актуальность настоящей работы обусловлена, с одной стороны, большим интересом к теме в современной науке, с другой стороны, ее недостаточной разработанностью. Рассмотрение вопросов, связанных с данной тематикой носит как теоретическую, так и практическую значимость.Объектом работы – случайные величиныПредмет работы – разыгрывание случайных величинЦелью исследования является изучение различных способов разыгрывание случайных величинВ рамках достижения поставленной цели были поставлены и решения следующие задачи:

1. 
   Изучить способы разыгрывания случайных величин.
   
2. 
   Привести примеры разыгрывания случайных величин.
   

Структура работы включает в себя введение, основную часть, заключение и список литературы.

1. Разыгрывание дискретной случайной величины

Пусть требуется разыграть дискретную случайную величину X, т.е. получить последовательность ее возможных значений 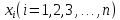, зная закон распределения X:

X			…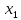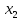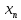
p			…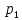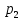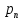

Обозначим через R непрерывную случайную величину, распределенную равномерно в интервале (0, 1), а через 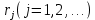возможные значения, т.е. случайные числа.Разобьем интервал 0 ≤ R < 1 на оси Or точками с координатами , , , …,

---

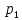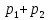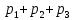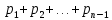
на n частичных интервалов ∆₁,∆₂,…,∆_n :

∆₁ = ,

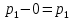∆₂= ,

…

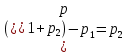∆_n = .

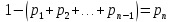Видим, что длина частичного интервала с индексом i равна вероятностей с тем же индексом: ∆_i = p_i. (*)

Теорема. Если каждому случайному числу r_i (0 ≤ r < 1), которое попало в интервал ∆_i, ставить в соответствие возможное значение х_i, то разыгрываемая величина будет иметь заданный закон распределения:

X			…
p			…

Доказательство. Т.к. при попадании случайного числа r_i в частичный интервал ∆_i, разыгрываемая величина принимает возможное значение х_i, а таких интервалов всего n, о разыгрываемая величина имеет те же возможные значения, что и Х, а именно х₁,х₂,…х_n.Вероятность попадания случайной величины R в интервал ∆_i, равна его длине, а в силу (*) ∆_i= p_i. Таким образом, вероятность попадания R в интервал ∆_i равна p_i. Следовательно, вероятность того, что разыгрываемая величина примет возможное значение х_i, также равна p_i, в силу того, что ранее мы условились, что в случае попадания случайного числа r_i в интервал ∆_i разыгрываемая величина примет возможное значение х_i. Итак, разыгрываемая величина имеет заданный закон распределения.Подводя общую черту, можно сформулировать следующее правило: для того, чтобы разыграть дискретную случайную величину, заданную законом распределения

X			…
p			…

---

нужно:

1. 
   Разбить интервал (0,1) оси Or на n частичных интервалов;
   
2. 
   Выбрать (из таблицы случайных чисел) случайное число r_j. Если r_j попало в частичный интервал ∆_i, то разыгрываемая дискретная случайная величина приняла возможно значение х_i.
   

Продемонстрируем применения правила на конкретном примере.Пример 1. Требуется разыграть 8 значение дискретной случайной величины Х, закон распределения которой задан в виде таблицы:

X	3	11	24
p	0,25	0,16	0,59

Решение.Первое что нужно сделать – это разбить интервал (0,1) оси Or точками с координатами 0,25; 0,25+0,16=0,41 на три частичных интервала ∆₁=(0;0,25), ∆₂=(0,25:0,41), ∆₃=(0,41;1).Выберем из таблицы случайных чисел 8 величин: 0,10; 0,37; 0,08; 0,99; 0,12; 0,66; 0,31; 0,85.Случайное число r₁ = 0,10 принадлежит частичному интервалу ∆₁, поэтому разыгрываемая дискретная случайная величина принимает возможное значение х₁=3. Случайное число r₂ = 0,37 принадлежит частичному интервалу ∆₂, поэтому разыгрываемая величина принимает возможное значение х₂ = 11. Аналогично можно получить остальные возможные значения.Таким образом, разыгранные возможные значения Х такие: 3, 11, 3, 24, 3, 24, 11,24.

2. Разыгрывание противоположных событий

Пусть требуется разыграть испытания, в каждом из которых событие А появляется с известной вероятностью p и, как следствие, не появляется с вероятностью q = 1 – p. Рассмотрим дискретную случайную величину Х с двумя возможными значениями (для определенности возьмем х₁=1, х₂=0) и соответствующими им вероятностями p₁ = p, p₂ = q. Будем считать, что если в испытание величина Х приняла возможное значение х₁=1, то событие А наступило; напротив, если в испытании величина Х приняла возможное значение х₂ = 0, то событие А не наступило, т.е. появилось противоположное событие 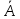.Итак, разыгрывание двух противоположных событий А и 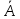сводится к разыгрыванию дискретной случайной величины Х с заданным законом распределения:

Х	1	0
p	P	q

---

Для разыгрывания Х нужно интервал (0,1) разбить точкой p на два частичных интервала ∆₁ = (0, p) и ∆₂ = (p, 1). Затем нужно выбрать случайное число r_j. Если r_jпопадет в ∆₁, то величина Х приняла значение х₁ и, следовательно, событие А наступило; если r_j попадет ∆₂, то Х=х₂ и событие А не наступило.Таким образом, можно сформулировать следующее правило: для того, чтобы разыграть испытание, в котором вероятность появления события равна p, а вероятность наступления противоположного события равна 1 – p, нужно выбрать (например, из таблицы случайных чисел) случайное число r_j (j=1,2,…); если r_j< p, то событие А наступило; если r_j ≥ p, то появилось противоположное событие .Приведем пример.Пример 2. Нужно разыграть 6 испытаний, в каждом из которых событие А появляется с вероятностью p = 0,35.Решение.Выберем из таблицы 6 случайных чисел: 0,10; 0,36; 0,08; 0,99; 0,12; 0,06. При условии, что при r_j < 0,35 событие А наступило, а при r_j≥ 0,35 наступило противоположное событие , получим следующую последовательность событий: А, , А, , А, А.

3. Разыгрывание полной группы событий

Разыгрывание полной группы n (n > 2) несовместных событий А₁, А₂, …, А_n вероятности которых соответственно равны p₁, p_{2, …} p_n, можно свести к разыгрыванию дискретной случайной величины Х со следующим законом распределения:

X	x1	x2	…	xn
p	p1	p2	…	pn

Будем считать, что если в испытании величина Х приняла значение x_i (i=1, 2, …, n), то наступило событие А_i. Это утверждение справедливо в силу того, что число n возможных значений Х равно числу событий полной группы и вероятности возможных значений х

---