Файл: Теория поведения производителя (теория производства). Выбор эффективной технологии производства.docx
Добавлен: 25.10.2023
Просмотров: 108
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Av является одновременно касательной к кривой совокупного продукта в этой точке.
Точка А3 на кривой совокупного продукта соответствует нулевому значению предельного продукта переменного фактора.
Таким образом, взаимосвязь между совокупным и предельным продуктами следующая:
Рациональный предприниматель будет всегда стремиться находиться на той стадии, когда использование каждой дополнительной единицы переменного фактора обеспечивает хотя и убывающий, но положительный прирост выпуска продукции.
Необходимо обратить внимание, что значение предельного продукта переменного фактора зависит от значений постоянных факторов производства. При изменении любого из постоянных факторов функция, определяющая зависимость объема производства от количества применяемого переменного фактора, принимает иной вид, отличный от первоначального.
В долгосрочном периоде все факторы переменны. Предположим, что цена ресурсов и количество денег, которыми располагает производитель, постоянны (заданы).
Введем следующие обозначения: — предельный продукт фактора на единицу стоимости фактора. Это показатель отдачи от единицы стоимости используемого фактора.
Правило наименьших издержек для долгосрочного периода: издержки минимизируются, если бюджет производителя распределен таким образом
, что каждая последняя денежная единица, затраченная на любой ресурс, дает одинаковую отдачу — одинаковый предельный продукт, т.е. предельный продукт фактора на единицу стоимости фактора для всех используемых факторов одинаков.
Для краткосрочного периода правило наименьших издержек формулируется следующим образом: издержки минимизируются, если бюджет производителя распределен таким образом, что каждая последняя денежная единица, затраченная на любой переменный ресурс, дает одинаковую отдачу — одинаковый предельный продукт, т.е. предельный продукт фактора на единицу стоимости фактора для всех переменных факторов одинаков.
Правило наименьших издержек характеризует равновесие производителя.
Используя правило наименьших издержек, мы выбираем экономически эффективный способ производства из множества технически эффективных.
Выделяют три этапа оптимального производственного выбора:
Далее в целях упрощения исследований будем рассматривать производственную функцию, состоящую всего из двух факторов — труда (L) и капитала (A): Q =f(L, К).
3.1 Анализ технологических возможностей производства
Целью исследований на данном этапе является определение различных комбинаций факторов, обеспечивающих один и тот же объем выпуска продукции. Геометрически это может быть отображено в виде изокванты и карты изоквант.
Изокванта — геометрическое место точек (кривая, линия), каждая из которых соответствует комбинации двух ресурсов труда (L) и капитала (К), способных произвести заданный объем выпуска продукции (Q) (рис. 9.2).
Для каждой точки изокванты выполняется равенство:
Q (LVKX) = Q (L2,K2) - const.
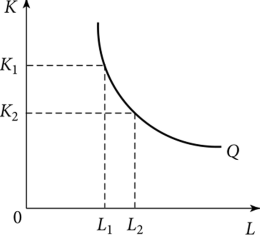
Рис. 9.2. Изокванта
Карта изоквант — это полная совокупность изоквант (рис. 9.3).
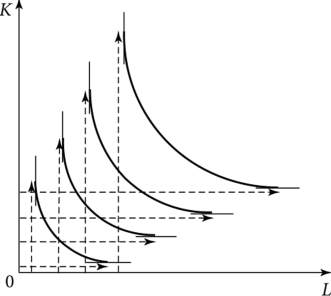
Рис. 9.3. Карта изоквант
Свойства изоквант:
Поскольку изокванты описывают только технически эффективные способы производства, мы не рассматриваем те участки, где МР одного из факторов принимает отрицательные значения. Соответственно, каждая изокванта будет ограничена и сверху и снизу точками, наклон которых равен наклону соответствующей оси координат. При этом чем дальше от начала координат, тем крайние точки каждой следующей изокванты будут более удалены от противолежащих осей координат, т.е. изокванты будут иметь большую длину.
Основное отличие изокванты в процессе производства от кривой безразличия в процессе потребления: изокванта показывает реальный уровень производства, а кривая безразличия — суммарную полезность, которую измерить нельзя.
При рассмотрении поведения производителя с помощью изоквант возникает вопрос: от какого количества одного ресурса может отказаться производитель, приобретая дополнительную единицу другого ресурса, чтобы при этом не изменился объем производства. Ответ на этот вопрос дает предельная норма технологического замещения (MRTS — marginal rate of technical substitution).
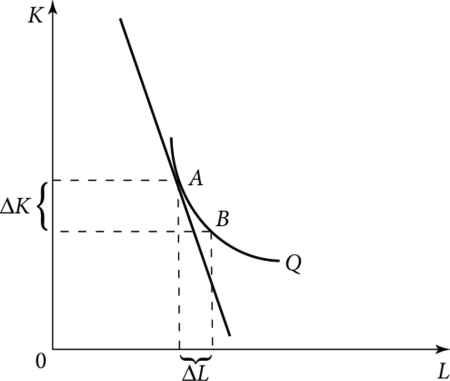
Рис. 9.4. Предельная норма технологического замещения. Стандартная форма изокванты (изокванта Кобба—Дугласа)
Предельная норма технологического (технического) замещения ресурсом «труд» ресурса «капитал» (MRTSLK) показывает, от какого количества фактора капитала может отказаться производитель, используя дополнительную единицу другого фактора — труда, так, чтобы объем выпуска продукции остался постоянным.
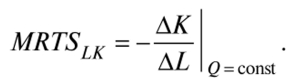
При малых AL предельная норма технологического замещения трудом капитала (MRTSLK) равна абсолютной величине наклона касательной к изокванте.
По мере увеличения использования фактора труда и уменьшения использования капитала величина предельной нормы технологического замещения убывает, а касательная становится все более пологой.
Такая ситуация характерна для стандартной формы изокванты (изокванты Кобба—Дугласа), которая и показана на рис. 9.4. Два фактора производства являются одновременно и заменителями и дополнителями друг другу. В определенных пределах мы можем заменить один фактор производства на другой
, но мы не можем полностью отказаться от одного из двух факторов.
Существуют и иные конфигурации изоквант (рис. 9.5).
На рис. 9.5(а) показана линейная изокванта. Два фактора производства являются совершенными заменителями при постоянной предельной норме их технического замещения (MRTS= const).
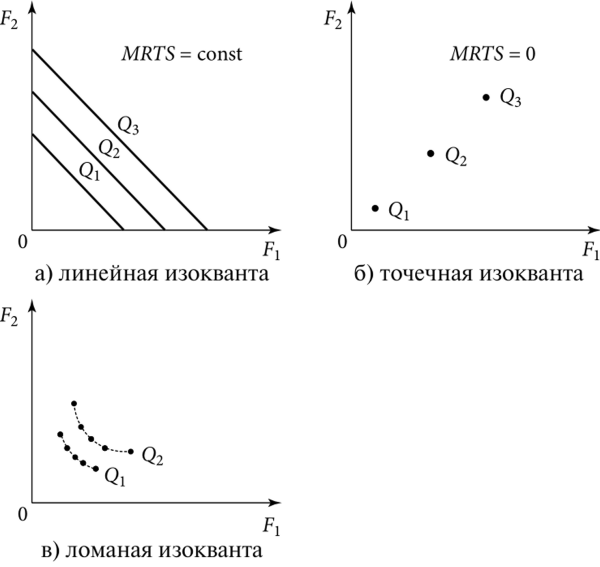
Рис. 9.5. Различные конфигурации изоквант
На рис. 9.5(б) изображена точечная изокванта. Два фактора производства являются совершенными дополнителями при нулевой предельной норме их технического замещения (MRTS = 0).
И наконец, на рис. 9.5(в) показана ломаная изокванта. Существует ограниченное количество сочетаний факторов производства для выпуска определенного объема продукции. Увеличивая количество способов производства, данная изокванта будет приближаться к изокванте Кобба—Дугласа.
Связь предельной нормы технического замещения с предельным продуктом
Выведем связь предельной нормы технического замещения с предельным продуктом.
Совокупный объем выпуска продукции в каждой точке изокванты (рис. 9.6) неизменен (Q — const). Следовательно, при перемещении из точки А в точку В, расположенных на одной изокванте, прирост объема выпуска от увеличения использования фактора L равен снижению объема выпуска от уменьшения использования фактора К. Отсюда получаем:
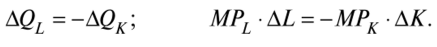
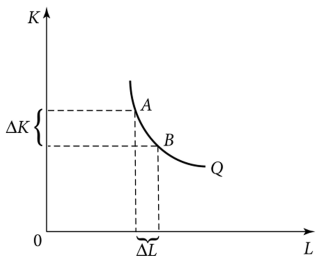
Рис. 9.6. Изокванта
Следовательно
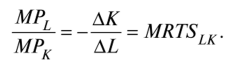
Таким образом, предельная норма технического замещения равна отношению предельных продуктов двух факторов производства:

Изокванты отражают технически эффективные способы производства. Однако при этом не учитывают два важных обстоятельства: цены ресурсов и бюджет производителя. Изокванты лишь показывают возможность замены одного ресурса другим без изменения уровня выпуска. Однако они не определяют, какой именно набор ресурсов считается экономически эффективным. Эту информацию нам поможет дать бюджетное ограничение.
Введем некоторые обозначения:
ТС (total cost) — совокупные (суммарные) издержки (денежный бюджет производителя, который может быть потрачен на приобретение любого набора факторов капитала и труда);
Рк, PL — цены соответствующих факторов (заданные величины);
КиЬ — количества каждого фактора (переменные величины).
Если бюджет будет потрачен полностью на приобретение любого набора факторов К и L, то бюджет производителя равен расходам на факторы:
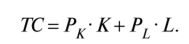
Выразив переменную величину капитала (Л) через величину труда (L), получим уравнение изокосты: К= ТС/РК— (РJРк) ? L (линейная функция).
Изокоста — геометрическое место точек (прямая), каждая из которых соответствует комбинации двух ресурсов, имеющих одинаковую суммарную стоимость, т.е. совокупные издержки на всей прямой постоянны.
Рассмотрим принцип построения линии изокосты (рис. 9.7). Точка пересечения изокосты с осью абсцисс находится при К= О, L = TC/PL, с осью ординат — при L = 0, К= ТС/РК. Угловой коэффициент прямой равен —PL/Рк.
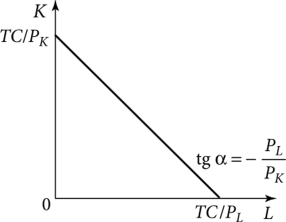
Рис. 9.7. Изокоста
Рассмотрим варианты сдвига изокосты при изменении бюджета производителя и цен на факторы.
Изокоста смещается:
1) при изменении бюджета производителя и постоянных ценах на факторы L, К. Исходная изокоста сдвигается, не изменяя наклона, вправо вверх (если бюджет увеличивается) или влево вниз (если бюджет уменьшается).
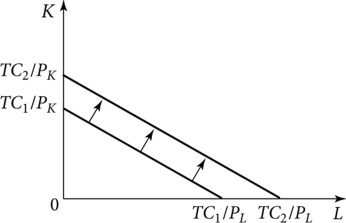
Рис. 9.8. Сдвиг изокосты при увеличении бюджета (ТС2 > ТС{)
На рис. 9.8 рассмотрен случай, когда при увеличении бюджета происходит сдвиг изокосты (ТС{/РК; TCJPL) параллельно исходной вправо вверх, и она принимает положение (ТС2/РК; TC2/PL);
2) при одновременном, равнократном изменении цены фактора L и цены фактора К и неизменном бюджете. Исходная изокоста сдвигается, не изменяя наклона, вправо вверх (при одновременном, равнократном уменьшении цен факторов L и К) или влево вниз (при одновременном, равнократном увеличении цен факторов
Точка А3 на кривой совокупного продукта соответствует нулевому значению предельного продукта переменного фактора.
Таким образом, взаимосвязь между совокупным и предельным продуктами следующая:
-
совокупный продукт максимален, когда предельный продукт переменного фактора равен нулю; -
совокупный продукт увеличивается, когда предельный продукт переменного фактора положителен; -
совокупный продукт уменьшается, когда предельный продукт переменного фактора отрицателен. -
Взаимосвязь между совокупным и предельным продуктами следующая: -
средний продукт максимален, когда предельный продукт оказывается равным среднему продукту; -
средний продукт увеличивается, пока предельный продукт больше среднего продукта; -
средний продукт уменьшается, когда предельный продукт меньше среднего продукта.
Рациональный предприниматель будет всегда стремиться находиться на той стадии, когда использование каждой дополнительной единицы переменного фактора обеспечивает хотя и убывающий, но положительный прирост выпуска продукции.
Необходимо обратить внимание, что значение предельного продукта переменного фактора зависит от значений постоянных факторов производства. При изменении любого из постоянных факторов функция, определяющая зависимость объема производства от количества применяемого переменного фактора, принимает иной вид, отличный от первоначального.
-
Правило наименьших издержек. Равновесие производителя
В долгосрочном периоде все факторы переменны. Предположим, что цена ресурсов и количество денег, которыми располагает производитель, постоянны (заданы).
Введем следующие обозначения: — предельный продукт фактора на единицу стоимости фактора. Это показатель отдачи от единицы стоимости используемого фактора.
Правило наименьших издержек для долгосрочного периода: издержки минимизируются, если бюджет производителя распределен таким образом
, что каждая последняя денежная единица, затраченная на любой ресурс, дает одинаковую отдачу — одинаковый предельный продукт, т.е. предельный продукт фактора на единицу стоимости фактора для всех используемых факторов одинаков.
Для краткосрочного периода правило наименьших издержек формулируется следующим образом: издержки минимизируются, если бюджет производителя распределен таким образом, что каждая последняя денежная единица, затраченная на любой переменный ресурс, дает одинаковую отдачу — одинаковый предельный продукт, т.е. предельный продукт фактора на единицу стоимости фактора для всех переменных факторов одинаков.
Правило наименьших издержек характеризует равновесие производителя.
Используя правило наименьших издержек, мы выбираем экономически эффективный способ производства из множества технически эффективных.
-
Второй способ определения равновесия производителя
Выделяют три этапа оптимального производственного выбора:
-
анализ технологических возможностей производства; -
анализ бюджетов производителя; -
оптимальный производственный выбор.
Далее в целях упрощения исследований будем рассматривать производственную функцию, состоящую всего из двух факторов — труда (L) и капитала (A): Q =f(L, К).
3.1 Анализ технологических возможностей производства
Целью исследований на данном этапе является определение различных комбинаций факторов, обеспечивающих один и тот же объем выпуска продукции. Геометрически это может быть отображено в виде изокванты и карты изоквант.
Изокванта — геометрическое место точек (кривая, линия), каждая из которых соответствует комбинации двух ресурсов труда (L) и капитала (К), способных произвести заданный объем выпуска продукции (Q) (рис. 9.2).
Для каждой точки изокванты выполняется равенство:
Q (LVKX) = Q (L2,K2) - const.

Рис. 9.2. Изокванта
Карта изоквант — это полная совокупность изоквант (рис. 9.3).

Рис. 9.3. Карта изоквант
Свойства изоквант:
-
Их может быть сколь угодно много. -
Изокванта, лежащая выше и правее другой кривой, соответствует большему объему выпуска. -
Они не пересекаются. -
Они имеют отрицательный наклон. -
Как правило, они выгнуты (выпуклы) к началу координат и становятся более пологими по мере продвижения вправо вследствие эффекта убывания предельного продукта.
Поскольку изокванты описывают только технически эффективные способы производства, мы не рассматриваем те участки, где МР одного из факторов принимает отрицательные значения. Соответственно, каждая изокванта будет ограничена и сверху и снизу точками, наклон которых равен наклону соответствующей оси координат. При этом чем дальше от начала координат, тем крайние точки каждой следующей изокванты будут более удалены от противолежащих осей координат, т.е. изокванты будут иметь большую длину.
Основное отличие изокванты в процессе производства от кривой безразличия в процессе потребления: изокванта показывает реальный уровень производства, а кривая безразличия — суммарную полезность, которую измерить нельзя.
При рассмотрении поведения производителя с помощью изоквант возникает вопрос: от какого количества одного ресурса может отказаться производитель, приобретая дополнительную единицу другого ресурса, чтобы при этом не изменился объем производства. Ответ на этот вопрос дает предельная норма технологического замещения (MRTS — marginal rate of technical substitution).

Рис. 9.4. Предельная норма технологического замещения. Стандартная форма изокванты (изокванта Кобба—Дугласа)
Предельная норма технологического (технического) замещения ресурсом «труд» ресурса «капитал» (MRTSLK) показывает, от какого количества фактора капитала может отказаться производитель, используя дополнительную единицу другого фактора — труда, так, чтобы объем выпуска продукции остался постоянным.
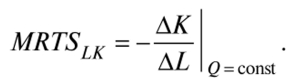
При малых AL предельная норма технологического замещения трудом капитала (MRTSLK) равна абсолютной величине наклона касательной к изокванте.
По мере увеличения использования фактора труда и уменьшения использования капитала величина предельной нормы технологического замещения убывает, а касательная становится все более пологой.
Такая ситуация характерна для стандартной формы изокванты (изокванты Кобба—Дугласа), которая и показана на рис. 9.4. Два фактора производства являются одновременно и заменителями и дополнителями друг другу. В определенных пределах мы можем заменить один фактор производства на другой
, но мы не можем полностью отказаться от одного из двух факторов.
Существуют и иные конфигурации изоквант (рис. 9.5).
На рис. 9.5(а) показана линейная изокванта. Два фактора производства являются совершенными заменителями при постоянной предельной норме их технического замещения (MRTS= const).

Рис. 9.5. Различные конфигурации изоквант
На рис. 9.5(б) изображена точечная изокванта. Два фактора производства являются совершенными дополнителями при нулевой предельной норме их технического замещения (MRTS = 0).
И наконец, на рис. 9.5(в) показана ломаная изокванта. Существует ограниченное количество сочетаний факторов производства для выпуска определенного объема продукции. Увеличивая количество способов производства, данная изокванта будет приближаться к изокванте Кобба—Дугласа.
Связь предельной нормы технического замещения с предельным продуктом
Выведем связь предельной нормы технического замещения с предельным продуктом.
Совокупный объем выпуска продукции в каждой точке изокванты (рис. 9.6) неизменен (Q — const). Следовательно, при перемещении из точки А в точку В, расположенных на одной изокванте, прирост объема выпуска от увеличения использования фактора L равен снижению объема выпуска от уменьшения использования фактора К. Отсюда получаем:

Рис. 9.6. Изокванта
Следовательно
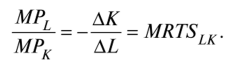
Таким образом, предельная норма технического замещения равна отношению предельных продуктов двух факторов производства:

-
Анализ бюджетов производителя
Изокванты отражают технически эффективные способы производства. Однако при этом не учитывают два важных обстоятельства: цены ресурсов и бюджет производителя. Изокванты лишь показывают возможность замены одного ресурса другим без изменения уровня выпуска. Однако они не определяют, какой именно набор ресурсов считается экономически эффективным. Эту информацию нам поможет дать бюджетное ограничение.
Введем некоторые обозначения:
ТС (total cost) — совокупные (суммарные) издержки (денежный бюджет производителя, который может быть потрачен на приобретение любого набора факторов капитала и труда);
Рк, PL — цены соответствующих факторов (заданные величины);
КиЬ — количества каждого фактора (переменные величины).
Если бюджет будет потрачен полностью на приобретение любого набора факторов К и L, то бюджет производителя равен расходам на факторы:
Выразив переменную величину капитала (Л) через величину труда (L), получим уравнение изокосты: К= ТС/РК— (РJРк) ? L (линейная функция).
Изокоста — геометрическое место точек (прямая), каждая из которых соответствует комбинации двух ресурсов, имеющих одинаковую суммарную стоимость, т.е. совокупные издержки на всей прямой постоянны.
Рассмотрим принцип построения линии изокосты (рис. 9.7). Точка пересечения изокосты с осью абсцисс находится при К= О, L = TC/PL, с осью ординат — при L = 0, К= ТС/РК. Угловой коэффициент прямой равен —PL/Рк.

Рис. 9.7. Изокоста
Рассмотрим варианты сдвига изокосты при изменении бюджета производителя и цен на факторы.
Изокоста смещается:
1) при изменении бюджета производителя и постоянных ценах на факторы L, К. Исходная изокоста сдвигается, не изменяя наклона, вправо вверх (если бюджет увеличивается) или влево вниз (если бюджет уменьшается).

Рис. 9.8. Сдвиг изокосты при увеличении бюджета (ТС2 > ТС{)
На рис. 9.8 рассмотрен случай, когда при увеличении бюджета происходит сдвиг изокосты (ТС{/РК; TCJPL) параллельно исходной вправо вверх, и она принимает положение (ТС2/РК; TC2/PL);
2) при одновременном, равнократном изменении цены фактора L и цены фактора К и неизменном бюджете. Исходная изокоста сдвигается, не изменяя наклона, вправо вверх (при одновременном, равнократном уменьшении цен факторов L и К) или влево вниз (при одновременном, равнократном увеличении цен факторов