ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
Введение 3
1 Теоретическая часть 5
1.2 Регрессия 5
1.2 Метод наименьших квадратов 6
2 Практическая часть 9
2.1 Линейная регрессия в АП Deductor 9
2.1.2 Настройка назначений полей 10
2.1.3 Разделение исходного набора наблюдений на обучающее и тестовое множества 11
2.1.4 Настройка ограничения диапазона выходных значений 11
2.1.5 Отбор переменных в регрессию 12
2.1.6 Запуск процесса обучения 14
2.1.7 Определение способов отображения 15
3 Экспериментальная часть 16
3.1. Исходные данные 16
3.2 Анализ результатов 17
Заключение 21
Список используемой литературы 22
Введение
Прогресс в информационной сфере немыслим без применения современных интеллектуальных информационных систем (ИС). ИС имеют дело с организацией и эффективной обработкой больших объемов разнородной информации в компьютеризированных системах предприятий, обеспечивая информационную поддержку принятия решений на всех уровнях управления. Использование интеллектуальных информационных систем в настоящее время является неотъемлемой частью функционирования большинства предприятий. Поэтому освоение интеллектуального анализа данных является нужной и востребованной задачей.
В методах интеллектуального анализа естественным образом сформировалась потребность в модели, реализующей численное предсказание и при этом являющейся содержательно интерпретируемой. Такая модель была «позаимствована» из математической статистики и носит название регрессия. Регрессия описывает зависимость между вектором входных переменных и выходной переменной, когда все переменные вещественные. Регрессия представляет собой один из наиболее ранних и хорошо разработанных методов исследования данных. Первые работы, в которых были изложены основы регрессии, а именно, метод наименьших квадратов, были опубликованы Лежандром (1807) и Гауссом (1809) в астрономических приложениях. [1].
Целью данной курсовой работы является ознакомление с одним из методов интеллектуального анализа данных: линейной регрессий, а также построение модели линейной регрессии в аналитической платформе Deductor.
Задачами данного курсового проекта являются:
-
изучение теоретического материала по линейной регрессии: -
изучение и описание реализации модели линейной регрессии в аналитической платформе Deductor: -
подготовка набора данных для построения модели линейной регрессии; -
построение модели линейной регрессии; -
анализ построенной модели; -
1 Теоретическая часть
1.2 Регрессия
Регрессия – это условное математическое ожидание непрерывной зависимой переменной при наблюдаемых значениях независимых переменных. Линейная регрессия основана на гипотезе, что искомая зависимость – линейная. Каждая независимая переменная вносит аддитивный вклад в результирующее значение с некоторым весом, называемом коэффициентом регрессии. Как правило входных параметров регрессии несколько.
Пусть имеется набор входных значений Xi, где i = 1 ... n, т.е X = {x1,x2, ... , xn}. Тогда можно указать такой набор выходных значений Yj (j = 1…m), который будет соответствовать линейной комбинации входных значений с коэффициентами аi (i = 1…n):
[1, x1, x2, ... , xn] [a0, a1, a2, ..., an] = [y1, y2 ,..., ym] (1)
Если для простоты предположить, что выходное значение одно, то можно записать:
a0 + x1a1 + x2a2 + …+ xnan = y (2)
Таким образом, задача сводится к подбору коэффициентов ai.
Создание регрессионной модели представляет собой итерационный процесс, направленный на поиск эффективных независимых переменных, чтобы объяснить зависимые переменные, которые мы пытаемся смоделировать или понять, запуская инструмент регрессии, чтобы определить, какие величины являются эффективными предсказателями. Затем пошаговое удаление и/или добавление переменных до тех пор, пока не будет подобрана наилучшим образом подходящая регрессионная модель
Линейная регрессия предназначена для получения прогноза непрерывных числовых переменных. Ее достоинства:
-
Скорость и простота получения модели. -
Интерпретируемость модели. Линейная модель является прозрачной и понятной для аналитика. По полученным коэффициентам регрессии можно судить о том, как тот или иной фактор влияет на результат, сделать на этой основе дополнительные полезные выводы. -
Широкая применимость. Большое количество реальных процессов в экономике и бизнесе можно с достаточной точностью описать линейными моделями. -
Изученность данного подхода. Для линейной регрессии известны типичные проблемы и их решения, разработаны и реализованы тесты оценки статической значимости получаемых моделей.
Недостатком регрессионной модели является то, что она не всегда пригодна для качественного предсказания зависимой переменной. Например, если выходная переменная является категориальной или бинарной, приходится использовать различные модификации регрессии.
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки используется метод наименьших квадратов (МНК)
1.2 Метод наименьших квадратов
Метод наименьших квадратов (МНК) — это математический подход для оценки параметров моделей на основании экспериментальных данных, содержащих случайные ошибки.
Пусть x — набор n неизвестных переменных (параметров), а
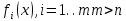 - совокупность функций от этого набора переменных.
- совокупность функций от этого набора переменных.Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым yi. То есть решается переопределенная система уравнений
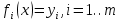 , в указанном смысле максимальной близости левой и правой частей системы. Суть МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей
, в указанном смысле максимальной близости левой и правой частей системы. Суть МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей 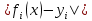 [3]. Таким образом, сущность МНК может быть выражена следующим образом:
[3]. Таким образом, сущность МНК может быть выражена следующим образом: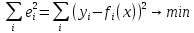 (3)
(3)В случае, если система уравнений имеет решение, то наименьшее значение суммы квадратов будет равно нулю, и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор x в смысле максимальной близости векторов y и f(x) или максимальной близости вектора отклонений e к нулю.
Например, предположим, что есть линейная модель yx=a+bx, необходимо определить конкретные значения коэффициентов модели. При различных значениях а и b можно построить бесконечное число зависимостей вида yx=a+bx т.е на координатной плоскости имеется бесконечное количество прямых, но необходимо найти такую зависимость, которая соответствует наблюдаемым значениям наилучшим образом[3].
Мерой рассогласования между фактическими значениями и значениями, оцененными моделью в методе наименьших квадратов, служит сумма квадратов разностей между ними, т.е.:
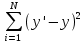 (4)
(4)где y′ — оценка, полученная с помощью модели, y — фактическое наблюдаемое значение. Очевидно, что лучшей будет та модель, которая минимизирует данную сумму.
2 Практическая часть
2.1 Линейная регрессия в АП Deductor
Deductor Studio – это программа, предназначенная для анализа информации из различных источников данных. Она реализует функции импорта, обработки, визуализации и экспорта данных. Deductor Studio может функционировать и без хранилища данных, получая информацию из любых других подключений, но наиболее оптимальным является их совместное использование.
Аналитическая платформа Deductor позволяет строить модели линейной регрессии на основе метода наименьших квадратов. Рассмотрим основные этапы построения модели линейной регрессии.
2.1.1 Подготовка и выбор алгоритма
На данном этапе необходимо выполнить следующие шаги:
1. Загрузить в аналитическое приложение исходный набор данных по указанию преподавателя.
2. Открыть Мастер обработки и в секции Data Mining выбрать пункт Линеная регрессия и нажать «далее».
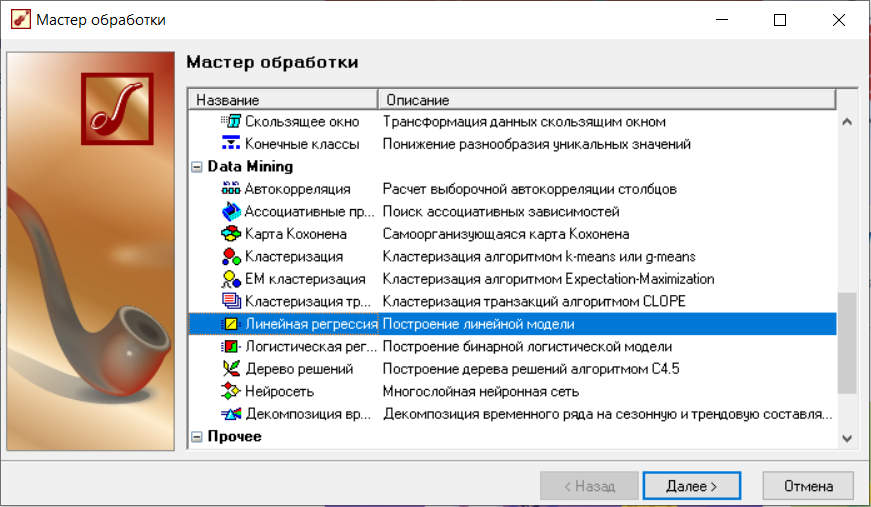
Рисунок 1 – Окно выбора мастера обработки
2.1.2 Настройка назначений полей
На данном шаге необходимо определить, как будут использоваться поля исходной выборки данных при построении линейной модели. В левой части окна приведен список всех полей исходной выборки данных. Поля бывают следующих типов (рисунок 2):
-
Информационное - поле не используется в процессе построения модели, но будет отображаться в результирующем наборе данных, полученном в результате кластеризации. Оно позволит помочь выполнить содержательную интерпретацию кластеров. -
Входное – поле будет содержать признаки, на основе которых будет производится кластеризация. -
Непригодное - поле не может быть использовано при построении и работе алгоритма, но будет включено в результирующую выборку без изменений. -
Выходное – значения поля будут использоваться как выходные (целевые)[2];
В качестве входных полей имеет смысл выбирать только те, которые отражают логику предметной области. Не следует использовать поля, содержащие порядковые номера или коды наблюдений, поскольку не отражают зависимости предметной области.
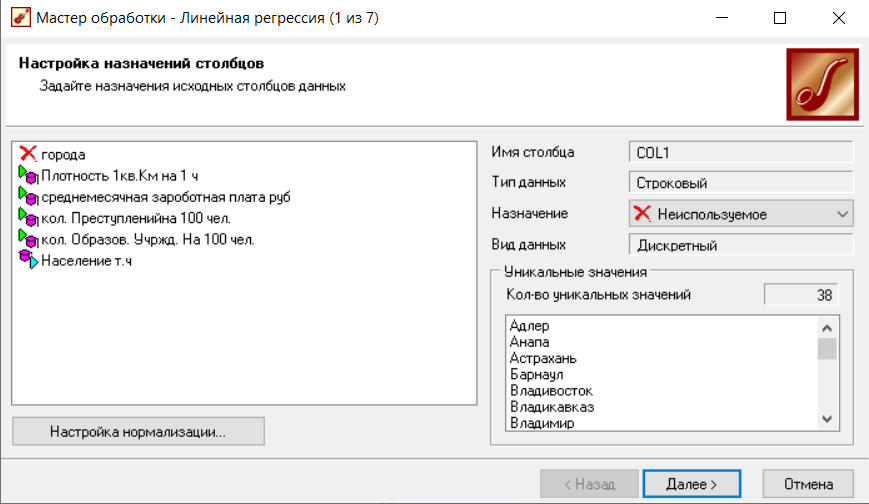
Рисунок 2 - Настройка назначения полей
2.1.3 Разделение исходного набора наблюдений на обучающее и тестовое множества
На данном этапе происходит разбиение исходных данных на два множества обучающее и тестовое. На обучающем множестве будет производится построение регрессионной модели, а на тестовом - проверка точности модели. (рисунок 3).
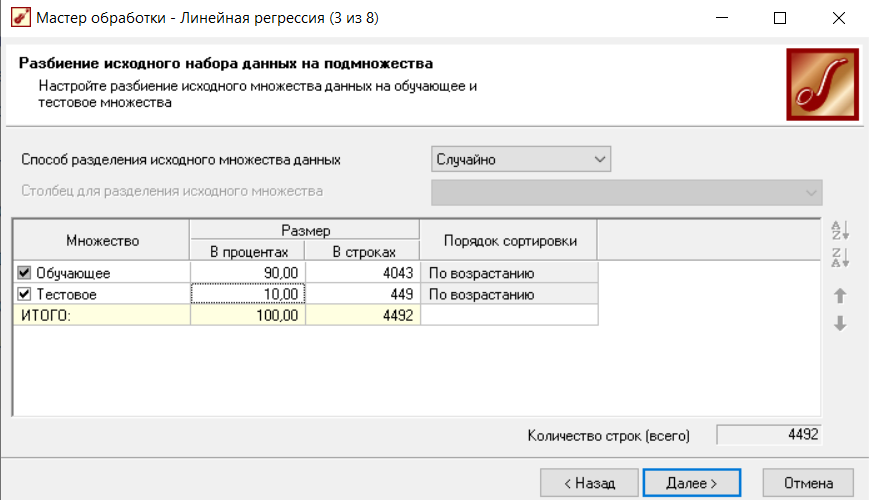
Рисунок 3 - Разбиение исходного набора данных
Размеры обучающего и тестового множеств могут быть заданы прямым указанием числа примеров, или их процентной доле от общего количества. Разделение на множества может производится в случайном порядке (рекомендуется), и последовательно, в порядке убывания или возрастания значений некоторого признака.
Как показывает практика, размер обучающего множества не должен превышать 10% от общего количества данных.
2.1.4 Настройка ограничения диапазона выходных значений
На данном этапе, при необходимости, можно указать ограничения, накладываемые на диапазон выходных значений (рисунок 4). Доступны следующие настройки диапазонов:
-
Абсолютный диапазон – указываются абсолютные значения минимума и максимума выходных значений; -
Относительный диапазон, % – указывается процент разброса относительно среднего значения. Разброс вычисляется по величине стандартного отклонения. -
Синхронно – при установке данного флага минимум и максимум диапазона выходного значения будут вычислены по одинаковой доле от стандартного отклонения[2];
Минимум/максимум – можно задать произвольные значения для определения краевых значений диапазона;
Среднее – среднее значение по полю в исходной выборке;
Стандартное отклонение – значение стандартного отклонения по полю в исходной выборке;
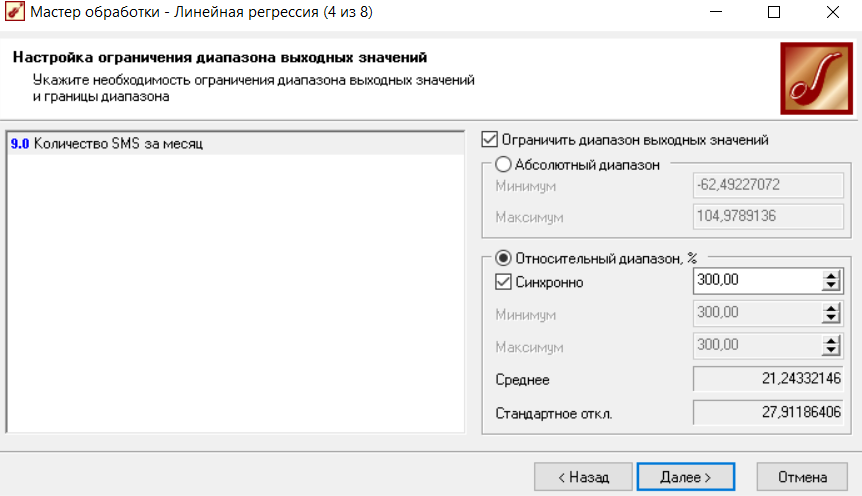
Рисунок 4 - Настройка ограничения диапазона выходных значений
2.1.5 Отбор переменных в регрессию
На данном этапе необходимо выбрать модель, согласно которой будет происходить отбор значимых для модели входных признаков. Сокращение числа независимых переменных необходимо для уменьшения размерности модели не только с тем, чтобы удалить из нее все незначащие признаки, не несущие в себе какой-то полезной для анализа информации, и тем самым упростить модель, но и чтобы устранить избыточные признаки. (рисунок 5)