ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 5 - Отбор переменных в регрессию
Первый метод осуществляется включение в регрессионную модель всех заданных признаков независимо от того, оказывают ли они значимое влияние или нет. Оставшиеся три метода основаны на критерии, называемом частный F – тест.
Критерий призван оценить целесообразность ввода дополнительной независимой переменной в линейную модель множественной регрессии.
В методе прямого отбора независимые переменные по порядку проверяются на значимость. Если ее значимость подтверждается, то она включается в модель.
Метод обратного исключения похож на предыдущий метод, но с тем отличием, что теперь уже изначально включены в модель все переменные и постепенно осуществляется "отсеивание" тех из них, которые не проходят проверку на значимость.
Метод последовательного отбора является модификацией метода прямого отбора, и отличается тем, что на каждом шаге после включения новой переменной в модель осуществляется проверка на значимость остальных переменных, которые уже были введены в нее ранее. Если такие переменные будут обнаружены, то их следует вывести из состава модели. После корректировки списка включенных в модель переменных осуществляется очередная итерация процедуры прямого отбора по поиску новой переменной, удовлетворяющей условиям включения ее в состав модели.
Параметры вероятность F включения переменной и вероятность F удаления переменной задают, соответственно, порог добавления ( в случае прямого и последовательного отбора) и удаления ( в случает обратного исключения) переменной.
2.1.6 Запуск процесса обучения
На данном шаге запускается процесс обучения модели линейной регрессии. (рисунок 6)
Рисунок 6. Запуск процесса обучения.
Для запуска процесса обучения следует нажать кнопку "Пуск". В любой момент процесс обучения может быть поставлен на паузу (временно приостановлен). Щелчок по кнопке "Пуск" после кнопки "Пауза" позволит продолжить построение кластерной модели. Кнопка "Стоп" прекращает процесс окончательно, без возможности его продолжения.
2.1.7 Определение способов отображения
На данном этапе требуется выбрать способы отображения результатов построения кластерной модели, которые позволяет оценить качество кластеризации и произвести содержательную интерпретацию кластеров (рисунок 6).
Рисунок 6 - Определение способов отображения
3 Экспериментальная часть
3.1. Исходные данные
В качестве эксперимента проанализируем статистические данные о городах (рисунок 7).
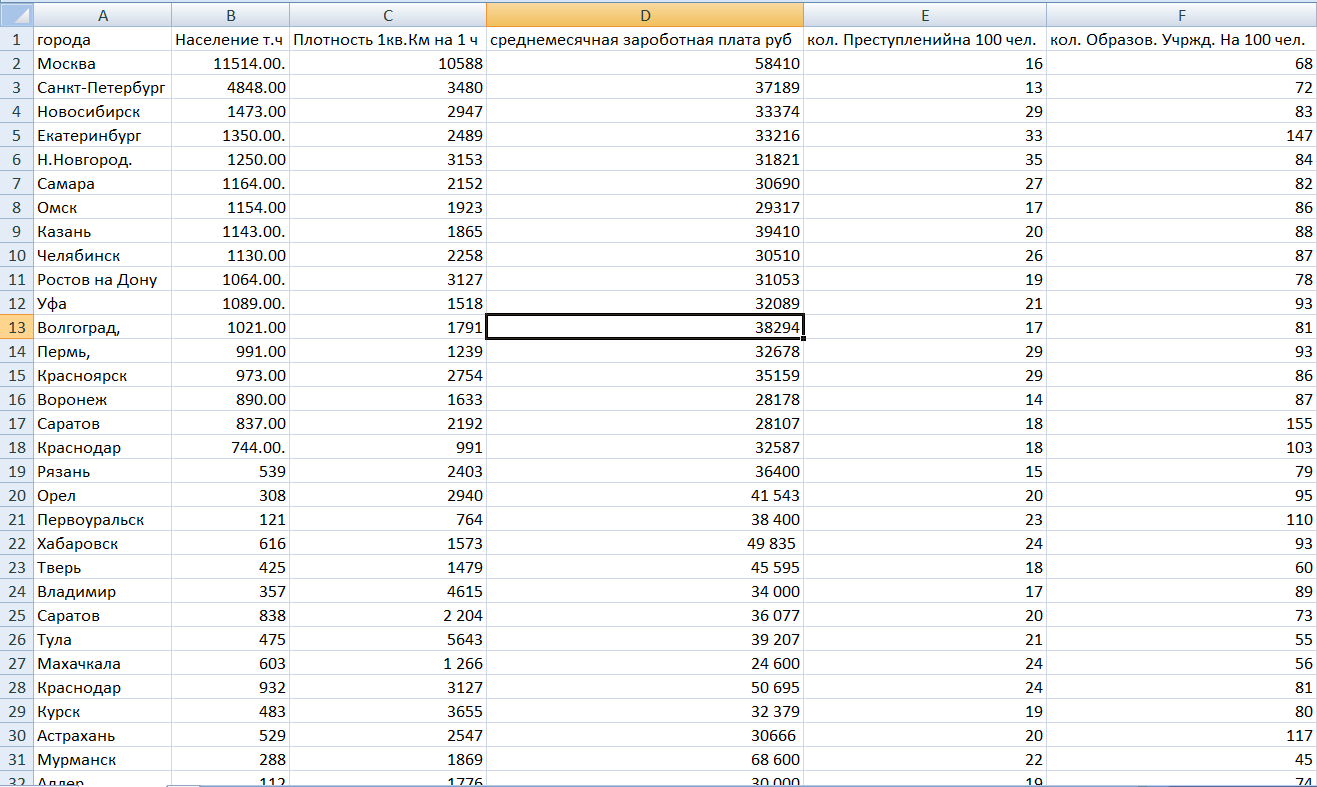
Рисунок 7 – исходные данные эксперимента
В рамках данного эксперимента, в качестве выходного поля возьмем переменную ‘население’, в качестве входных полей будем использовать все остальные переменные (рисунок 8).
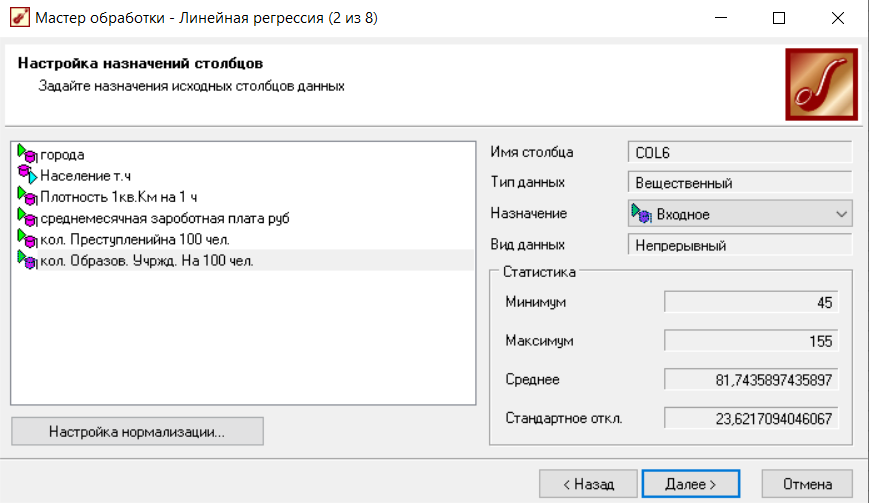
Рисунок 8 – настройка назначений столбцов
3.2 Анализ результатов
В результате построения регрессионной модели с полным включением были получены следующие результаты: диаграмма рассеивания (рисунок 9) и отчет по регрессии (рисунок 10).
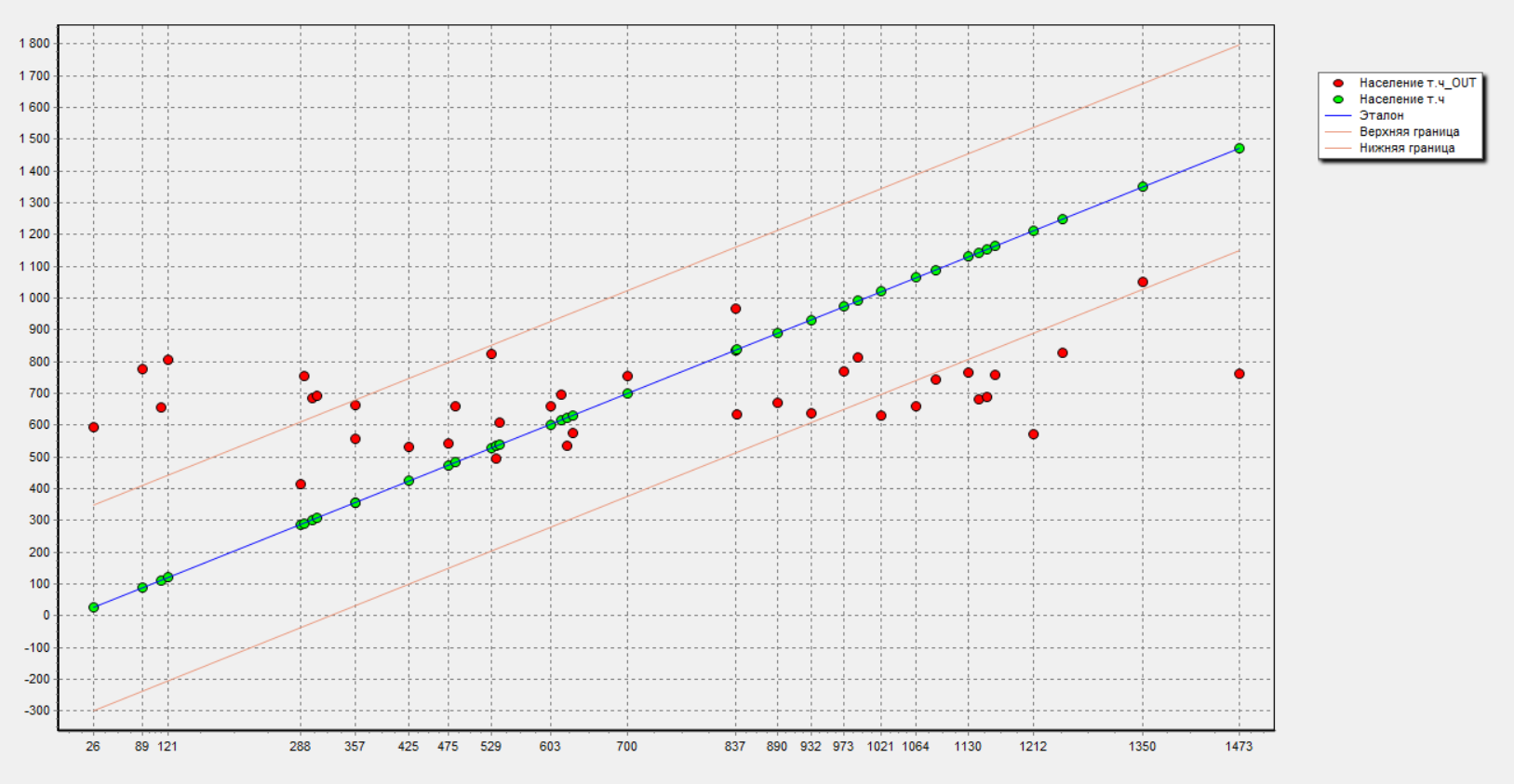 Рисунок 9 – Диаграмма рассеивания регрессионной модели
Рисунок 9 – Диаграмма рассеивания регрессионной модели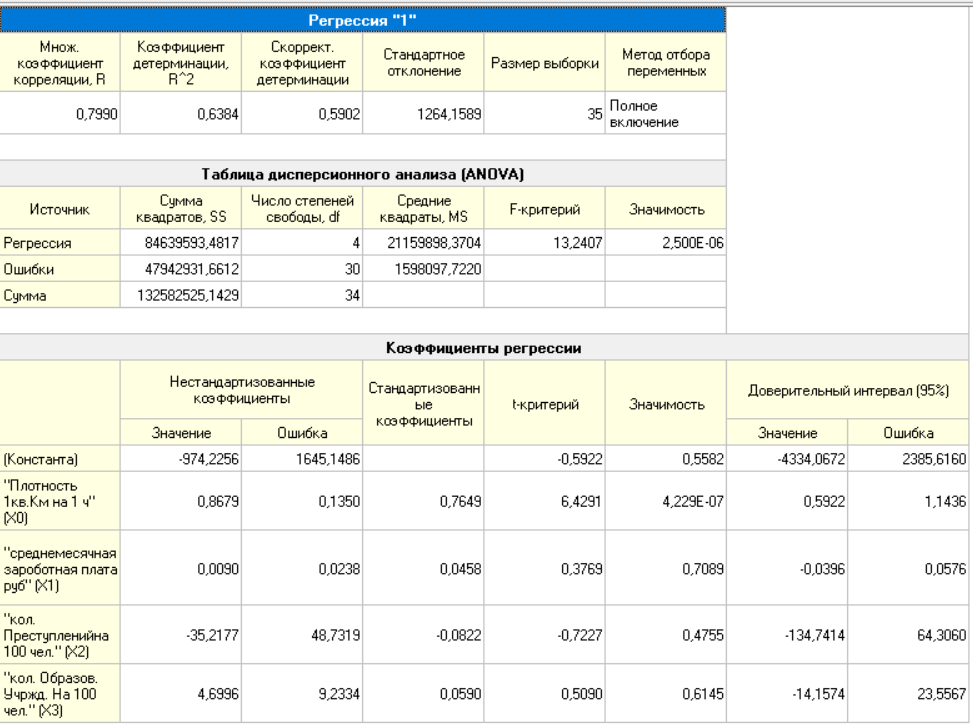
Рисунок 10 – Отчет по регрессии
Из полученных значений множественного коэффициента корреляции (0,7990) и коэффициента детерминации (0,6384) можно сделать вывод, что модель является приемлемой. Наиболее значимым параметром является плотность населения, а наименее значимым – количество преступлений.
Проанализируем, как будут изменяться параметры при изменении модели отбора переменных и соответствующих коэффициентов в них.
При анализе модели будем смотреть на коэффициенты корреляции и детерминации, а также полученные коэффициенты регрессии.
Коэффициент корреляции - показывает тесноту линейной взаимосвязи. Коэффициент детерминации рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели.
Коэффициент - детерминации показывает, какая доля вариации объясняемой переменной y учтена в модели и обусловлена влиянием на нее факторов, включенных в модель.
Таблица 1 – значения коэффициентов при изменении вероятности F включения переменной
| Вероятность F включения переменной | коэф. корреляции, R | коэф. детерминации, R2 | Плотность 1кв. км на 1 чел. | среднемесячная заработная плата | Количество преступлений на 100 чел. | Количество образовательных Учреждений на 100 чел. | Константа |
| 0,15 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9008 |
| 0,30 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9008 |
| 0,45 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9008 |
| 0,60 | 0,7887 | 0,6221 | 0,8914 | 0 | -28,5524 | 0 | -539,5025 |
| 0,75 | 0,7899 | 0,6240 | 0,8746 | 0,0091 | -26,7650 | 0 | -869,8002 |
Таблица 2 – значения коэффициентов при изменении вероятности F удаления переменной
| Вероятность F удаления переменной | коэф. корреляции, R | коэф. детерминации, R2 | Плотность 1кв. км на 1 чел. | среднемесячная заработная плата | Количество преступлений на 100 чел. | Количество образовательных Учреждений на 100 чел. | Константа |
| 0,15 | 0,7840 | 0,6146 | 0,9053 | 0 | 0 | 0 | -1223,7100 |
| 0,30 | 0,7840 | 0,6146 | 0,9053 | 0 | 0 | 0 | -1223,7100 |
| 0,45 | 0,7840 | 0,6146 | 0,9053 | 0 | 0 | 0 | -1223,7100 |
| 0,60 | 0,7870 | 0,6194 | 0,8901 | 0 | -26,1876 | 0 | -612,6673 |
| 0,75 | 0,7885 | 0,6217 | 0,8721 | 0,0100 | -24,3331 | 4,6996 | -975,2643 |
Таблица 3 – значения коэффициентов при изменении вероятности F включения и удаления переменной
| Вероятность F включения переменной | Вероятность F удаления переменной | коэф. корреляции, R | коэф. детерминации, R2 | Плотность 1кв. км на 1 чел. | среднемесячная заработная плата | Количество преступлений на 100 чел. | Количество образовательных Учреждений на 100 чел. | Константа |
| 0,15 | 0,90 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9 |
| 0,30 | 0,80 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9 |
| 0,45 | 0,70 | 0,7852 | 0,6165 | 0,9077 | 0 | 0 | 0 | -1208,9 |
Как видно, чем больше значение вероятности, тем большее параметров учитывается в регрессионной модели. Исходя из результатов построения модели с использованием различных моделей параметров отбора параметров, можно сделать вывод, что регрессионную модель можно построить, используя два параметра: «плотность населения» и «количество преступлений на 100 человек». При этом модель практически не потеряет в качестве, относительно полного включения параметров.
При этом стоит отметить, что наиболее точная модель получится, используя метод полного включения, что вполне логично. Прочие же методы необходимо применять при большом количестве входных параметров, чтобы уменьшить количество выходных коэффициентов, тем самым уменьшив сложность уравнения.
Заключение
В результате выполнения данной работы были изучена линейная регрессия и ее реализация в приложении Deductor Studio. В рамках изучения был подготовлен набор данных для моделирования, а также произведено построение модели линейной регрессии и ее анализ.
Список используемой литературы
-
Интеллектуальные системы и нечеткая логика: Учебник / В.П. Корячко, М.А. Бакулева, В.И. Орешков — М.: КУРС, 2017 — 352 с. -
Регрессионный анализ в Deductor Studio / Яковлев В.Б., Яковлев И.В. – M.:Lambert Academic Publishing, 2017 – 129c -
Основы линейного и нелинейного регрессионного и корреляционного анализов / Баранова И.М., Часова Н.А., 2007