ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 378
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«РЯЗАНСКИЙ ГОСУДАРСТВЕННЫЙ РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. В.Ф. Уткина»
Кафедра «САПР»
К ЗАЩИТЕ
Руководитель КП
___________
А.А. Митрошин
«__» _____ 2021 г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ
по дисциплине
«Интеллектуальные системы и мягкие вычисления»
Тема
«Исследование алгоритма нечеткой кластеризации»»
Выполнил ст. гр. 045М
Губанов Е.А. __________________
дата сдачи на проверку, подпись
Руководитель проекта
к.т.н., доц. Митрошин А.А. _____ __________________
оценка дата защиты, подпись
Рязань 2021 г.
Оглавление
Оглавление 2
Введение 3
Классификация алгоритмов 4
Алгоритм нечёткой кластеризации 6
Нечеткая кластеризация в SciLab 9
Функция fcmeans 10
Функция subclust 11
Функция inwichclust 13
Практическое выполнение нечеткой кластеризации в SciLab 15
Заключение 18
Список литературы 19
Введение
Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.
Применение кластерного анализа в общем виде сводится к следующим этапам:
-
Отбор выборки объектов для кластеризации. -
Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных. -
Вычисление значений меры сходства между объектами. -
Применение метода кластерного анализа для создания групп сходных объектов (кластеров). -
Представление результатов анализа.
После получения и анализа результатов возможна корректировка выбранной метрики и метода кластеризации до получения оптимального результата.
В данной курсовой работе будут рассмотрены алгоритмы нечеткой кластеризации, и их реализация в системе компьютерной математики SciLab.
Классификация алгоритмов
Для себя я выделил две основные классификации алгоритмов кластеризации.
Иерархические и плоские.
Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера.
Плоские алгоритмы строят одно разбиение объектов на кластеры.
Четкие и нечеткие.
Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.
Области использования задачи кластеризации в информатике.
Кластеризация результатов поиска — используется для «интеллектуальной» группировки результатов при поиске файлов, веб-сайтов, других объектов, предоставляя пользователю возможность быстрой навигации, выбора заведомо более релевантного подмножества и исключения заведомо менее релевантного — что может повысить юзабилити интерфейса по сравнению с выводом в виде простого сортированного по релевантности списка.
-
Clusty — кластеризующая поисковая машина компании Vivísimo -
Nigma — российская поисковая система с автоматической кластеризацией результатов -
Quintura — визуальная кластеризация в виде облака ключевых слов
Сегментация изображений (англ. image segmentation) — кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ (англ. edge detection) или распознавания объектов.
Интеллектуальный анализ данных (англ. data mining) — кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов
, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию.
Алгоритм нечёткой кластеризации
FCM-алгоритм кластеризации
Алгоритм нечеткой кластеризации называют FCM-алгоритмом (Fuzzy Classifier Means, Fuzzy C-Means). Целью FCM-алгоритма кластеризации является автоматическая классификация множества объектов, которые задаются векторами признаков в пространстве признаков. Другими словами, такой алгоритм определяет кластеры и соответственно классифицирует объекты. Кластеры представляются нечеткими множествами, и, кроме того, границы между кластерами также являются нечеткими.
FCM-алгоритм кластеризации предполагает, что объекты принадлежат всем кластерам с определенной ФП. Степень принадлежности определяется расстоянием от объекта до соответствующих кластерных центров. Данный алгоритм итерационно вычисляет центры кластеров и новые степени принадлежности объектов.
Для заданного множества К входных векторов хk и N выделяемых кластеров сj предполагается, что любой хк принадлежит любому сj с принадлежностью µjk интервалу [0,1], где j – номер кластера, а k – номер входного вектора.
Принимаются во внимание следующие условия нормирования для µjk:
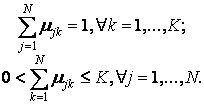
Цель алгоритма – минимизация суммы всех взвешенных расстояний
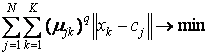
где q – фиксированный параметр, задаваемый перед итерациями.
Для достижения вышеуказанной цели необходимо решить следующую систему уравнений:
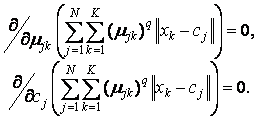
Совместно с условиями нормирования µjk данная система дифференциальных уравнений имеет следующее решение:
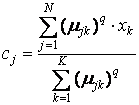
(взвешенный центр гравитации) и

Алгоритм нечеткой кластеризации выполняется по шагам
Шаг 1. Инициализация.
Выбираются следующие параметры:
• необходимое количество кластеров N, 2 < N < К;
• мера расстояний, как Евклидово расстояние;
• фиксированный параметр q (обычно 1,5);
• начальная (на нулевой итерации) матрица принадлежности
Шаг 2. Регулирование позиций
На t-м итерационном шаге при известной матрице
Шаг 3. Корректировка значений принадлежности µjk.
Учитывая известные
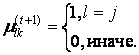
Шаг 4. Остановка алгоритма.
Алгоритм нечеткой кластеризации останавливается при выполнении следующего условия:
где || || – матричная норма (например, Евклидова норма);
ԑ – заранее задаваемый уровень точности.
Нечеткая кластеризация в SciLab
Для того, чтобы решать задачи нечеткой кластеризации в системе компьютерной математики Scilab, необходима установка необходимого модуля, который носит название SciFLT (Sci Fuzzy Logic Toolbox). Для его установки необходимо в главном меню выбрать пункт «Инструменты», затем в выпадающем меню выбрать пункт «Управление модулями Atoms» (рисунок 1).
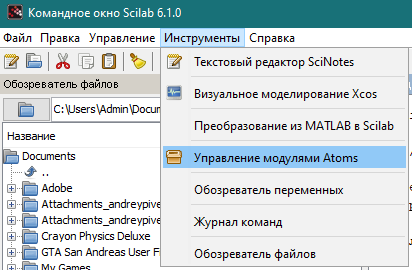
Рисунок 1 – Меню SciLab
В открывшемся окне, в списке необходимо открыть каталог со всеми доступными модулями и найти среди них модуль с названием «Fuzzy Logic Toolbox». Затем выбрать его и нажать кнопку «Установить» (рисунок 2).
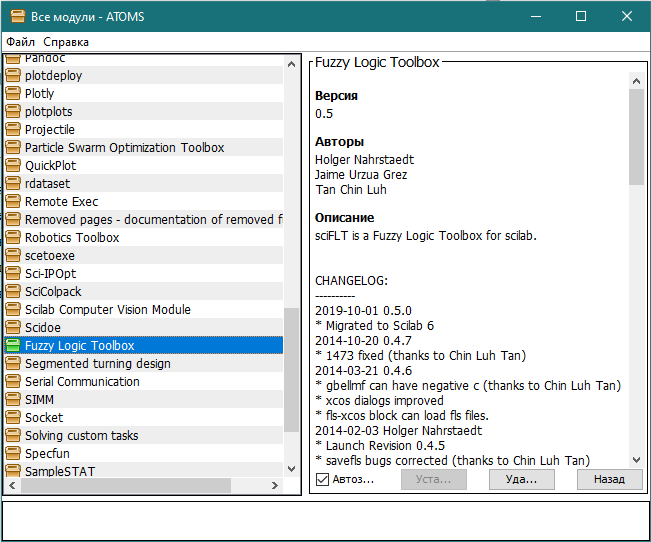
Рисунок 2 – модуль Fuzzy Logic Toolbox
После его установки необходимо перезапустить систему SciLab. После этого функции представленные в модуле будут доступны для использования. Рассмотрим несколько функций предназначенных для решения задач нечеткой кластеризации.
Функция fcmeans
Данная функция предназначена для нечеткой кластеризации FCM алгоритмом.
Прототип функции:
[centers,U,ofun,ofunk,em]=fcmeans(Xin,c,m [,maxiter [,epsilon [,verbose]]])
Параметры
-
Xin: матрица вещественных чисел. Пары входных точек. -
C: число кластеров. -
m: вещественный параметр нечеткости. -
maxiter: целое число итераций, по умолчанию равен 100. -
epsilon: вещественное число определяющее точность, т.е. минимальную разницу между значениями двух соседних итераций. По умолчанию равен 0.001 -
verbose: логическая переменная определяющая вывод информации. По умолчанию равен FALSE.
Функция fcmeans находит c количество кластеров в наборе данных Xin используя алгоритм нечеткой кластеризации (Fuzzy C-Means algorithm). Центры каждого кластера помещаются в выходной параметр centers. Выходной параметр U содержит степень вхождения каждой точки из Xin в каждый кластер. Выходной параметр ofun содержит последнее значение целевой функции. Выходной параметр ofunk содержит значения целевой функции в каждой итерации. Параметр em определяет режим завершения вычислений. Если установить значение em в TRUE тогда вычисление завершаться, как только количество итераций достигнут значения maxiter, если установить значение в FALSE, тогда вычисления завершаться, как только минимальная разница значений целевой функций между соседними итерациями будет меньше значения epsilon.
Пример:
// 50 случайных точек
Xin=rand(100,2);
// поиск 7 кластеров
[centers,U,ofun,ofunk]=fcmeans(Xin,7,2);
// Вывод информации
scf();clf();
subplot(2,2,1);
plot2d(Xin(:,1),Xin(:,2),-1,rect=[0 0 1 1]);
xtitle("Входные точки","x","y");
subplot(2,2,3);
plot2d(centers(:,1),centers(:,2)