ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 379
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,-2,rect=[0 0 1 1]);
xtitle("Центры кластеров","x","y");
subplot(2,2,2);
plot(ofunk);
xtitle("Значение целевой функции в каждой итерации","k","ofun");
Результат выполнения примера представлен на рисунке 1.
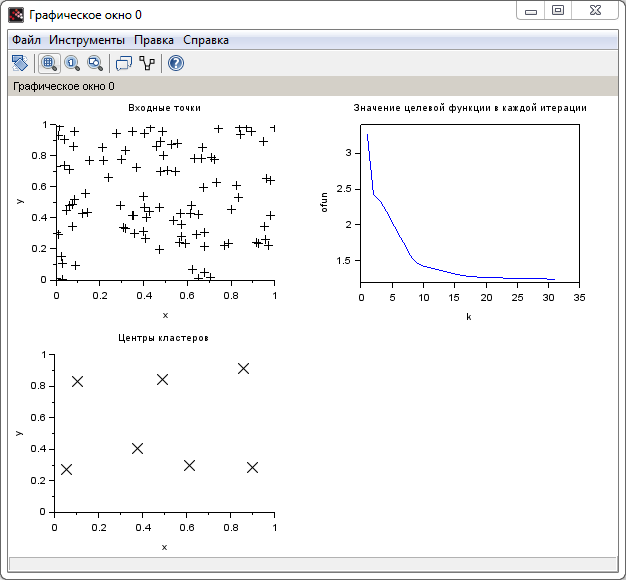
Рисунок 3 – Результат выполнения функции fcmeans
Из примера можно видеть, что в результате мы получили три графика. На верхнем левом изображены исходные пары точек, к которым применяется алгоритм нечеткой кластеризации. На верхнем правом графике изображены значения целевой функции на каждой итерации. На нижнем левом графике изображены точки полученных кластеров.
Данная функция предназначена для нахождения центров кластеров с вычитающей кластеризацией.
Прототип функции:
[centers,sigmas]=subclust(X [,r [, opt ]])
Параметры
Функция subclust позволяет найти центры кластеров с субстративной кластеризацией для матрицы X, в которой каждая строка содержит точку данных. r – это вектор, который определяет диапазон влияния центра кластера в каждом из измерений данных, предполагая, что данные попадают в единичный гипербокс (интернализированный).
opt=[ACCEPT_RATIO, REJECT_RATIO, REDUCTION_RATIO]. Если opt не предусмотрен, то в подпрограмме используются следующие параметры: ACCEPT_RATIO=0.5, REJECT_RATIO=0.15, REDUCTION_RATIO=1.5.
Пример:
// Возьмем 400 случайных пар точек с центрами в (0,0), (3,3), (7,7) и (10,10)
Xin=[rand(100,2);3+rand(100,2);7+rand(100,2);10+rand(100,2)];
// Находим кластеры
centers=subclust(Xin);
Результат выполнения примера представлен на рисунке 11.

Рисунок 4 – Результат выполнения функции subclust
Данная функция предназначена для нахождения ассоциированного с точкой кластера.
Прототип функции:
po=inwichclust(X,centers)
Параметры:
Функция inwichclust возвращает позицию ближайшего центра кластера для каждой пары точек из Х.
Пример:
// Сгенерируем 10 точек с центром (1,1) (2,2) и (5,5)
X=[1+rand(10,2);2+rand(10,2);5+rand(10,2)];
centers=subclust(X);
po=inwichclust(X,centers);
Рисунок 5 – Результат выполнения функции inwichclust
Решим задачу нечеткой кластеризации на примере реальных данных. В качестве исходных данных возьмем результаты агрохимического исследования почвы (рисунок 6).
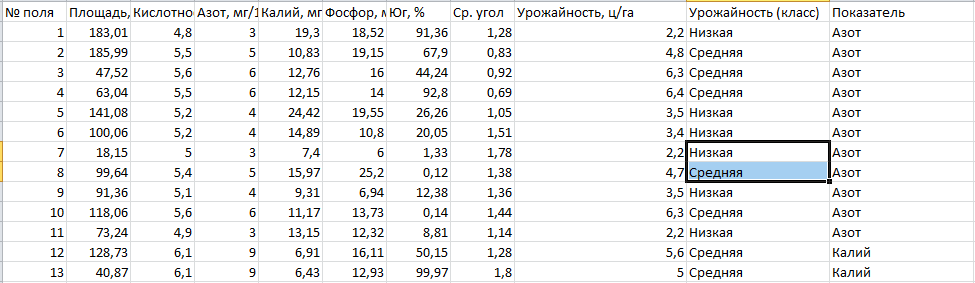
Рисунок 6 – Результаты агрохимического исследования почвы.
Для поиска кластеров будем пользоваться функций fcmeans. Для начала произведем алгоритм нечеткой кластеризации для значений калия в почве.
Результаты выполнения нечеткой кластеризации представлены на рисунке 7.
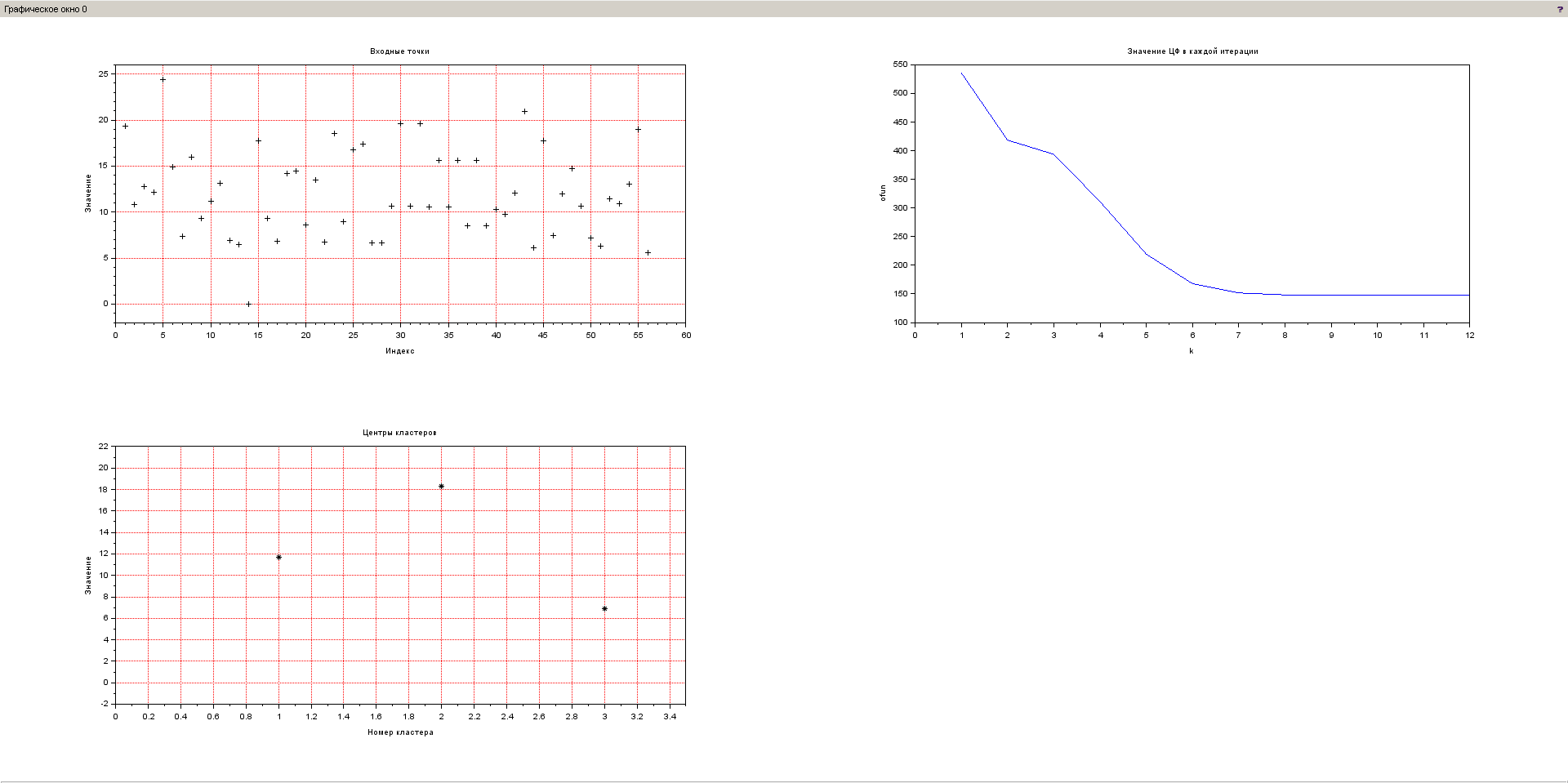
Рисунок 7 – Результат выполнения нечеткой кластеризации для данных о содержании калия в почве
Исходя из графика видно, что образуется три кластера, значения каждого из которых соответственно равны: 11.69, 18.28 и 6.92.
Произведем аналогичный анализ для данных о содержании фосфора в почве. Результат выполнения представлен на рисунке 8.
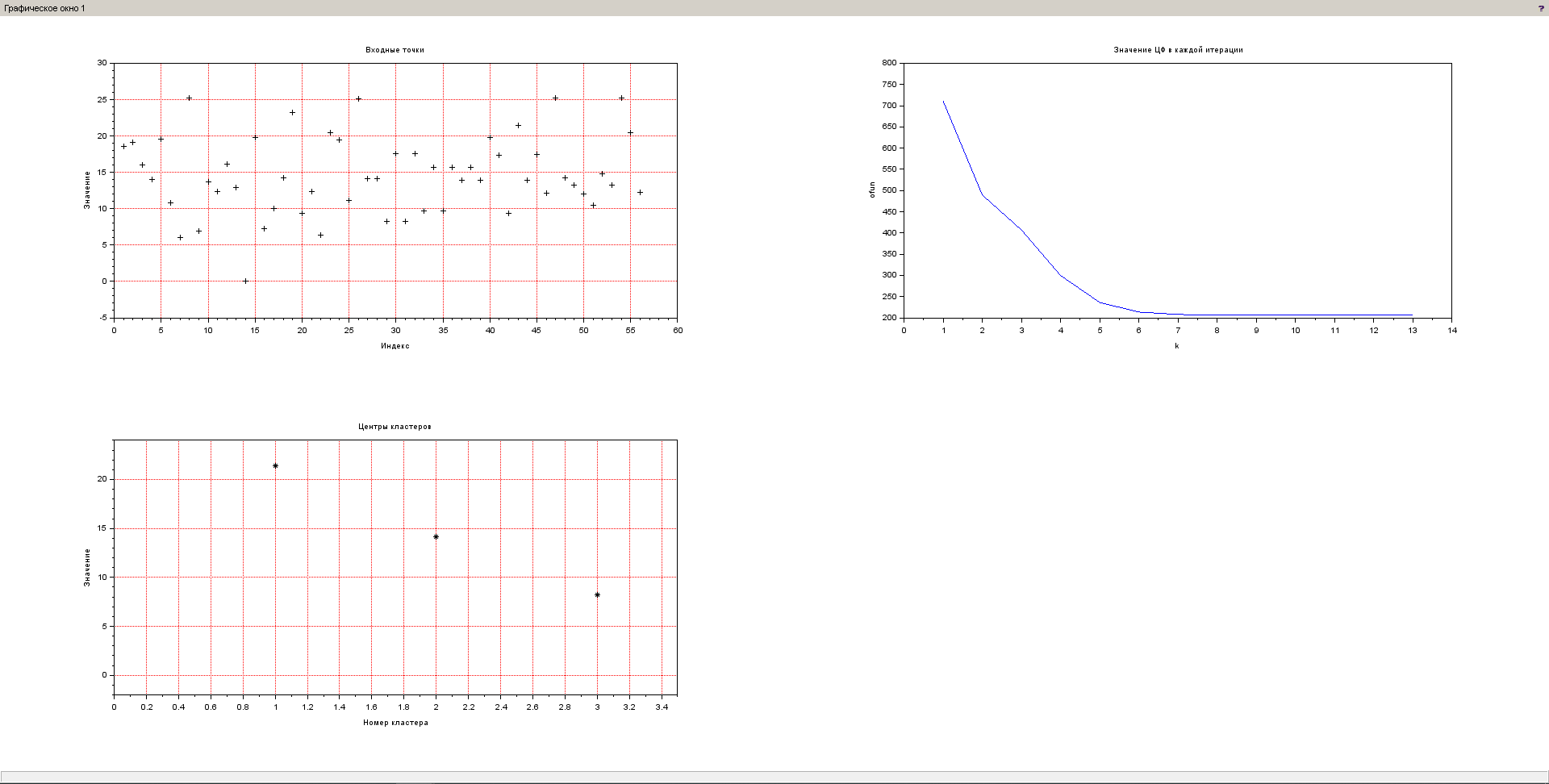
Рисунок 8 – Результат выполнения нечеткой кластеризации для данных о содержании фосфора в почве
Исходя из графика видно, что образуется три кластера, значения каждого из которых соответственно равны: 21.38, 14.13 и 8.24.
Листинг программы:
clear()
clc()
//Путь к файлу с данными
filename = fullfile("C:","\Scilab","\Fosfor.txt");
//Считываем данные из файла
Xin=fscanfMat(filename);
//Запоминаем максимальное, минимальное значение в файлах и его длину
//это необходимо для более удобного отображения графика
mmax=max(Xin);
mmin=min(Xin);
len=length(Xin);
//выполняем нечеткую кластеризацию
[centers,U,ofun,ofunk]=fcmeans(Xin,3,2);
// выводим информацию
scf();
clf();
subplot(2,2,1);
plot(Xin(:,1),'black+');
a=gca();
a.data_bounds=[0,mmin-0.05;len,mmax];
xgrid(5, 1, 7);
xtitle("Входные точки","Индекс","Значение");
subplot(2,2,3);
plot(centers(:,1),'black*');
a=gca();
a.data_bounds=[0,-1;length(centers)+0.01,max(centers(:,1))+2];
xgrid(5, 1, 7)
xtitle("Центры кластеров",'Номер кластера',"Значение");
subplot(2,2,2);
plot(ofunk);
xtitle("Значение ЦФ в каждой итерации","k","ofun");
В результате проведенного исследования мы выяснили задачи и цели кластеризации, в частности нечеткой кластеризации. Познакомились с системой компьютерной математики SciLab и рассмотрели способы решения задач нечеткой кластеризации на основе реальных данных.
В заключение можно сказать, что нечеткая кластеризация позволяет давать ответы на вопросы, когда данные описывают объекты или процессы в условиях неопределенности. Например, когда требуется оценить, болезненность цвета лица пациента, кредитоспособность заемщика, качество изделия и др..
xtitle("Центры кластеров","x","y");
subplot(2,2,2);
plot(ofunk);
xtitle("Значение целевой функции в каждой итерации","k","ofun");
Результат выполнения примера представлен на рисунке 1.

Рисунок 3 – Результат выполнения функции fcmeans
Из примера можно видеть, что в результате мы получили три графика. На верхнем левом изображены исходные пары точек, к которым применяется алгоритм нечеткой кластеризации. На верхнем правом графике изображены значения целевой функции на каждой итерации. На нижнем левом графике изображены точки полученных кластеров.
Функция subclust
Данная функция предназначена для нахождения центров кластеров с вычитающей кластеризацией.
Прототип функции:
[centers,sigmas]=subclust(X [,r [, opt ]])
Параметры
-
X: матрица вещественных чисел. Пары входных точек. -
r: вектор вещественных чисел. -
opt: трехэлеметный массив вещественных чисел. -
centers: центры кластеров. -
sigmas: вещественное число определяющее точность, т.е. минимальную разницу между значениями двух соседних итераций. По умолчанию равен 0.001
Функция subclust позволяет найти центры кластеров с субстративной кластеризацией для матрицы X, в которой каждая строка содержит точку данных. r – это вектор, который определяет диапазон влияния центра кластера в каждом из измерений данных, предполагая, что данные попадают в единичный гипербокс (интернализированный).
opt=[ACCEPT_RATIO, REJECT_RATIO, REDUCTION_RATIO]. Если opt не предусмотрен, то в подпрограмме используются следующие параметры: ACCEPT_RATIO=0.5, REJECT_RATIO=0.15, REDUCTION_RATIO=1.5.
Пример:
// Возьмем 400 случайных пар точек с центрами в (0,0), (3,3), (7,7) и (10,10)
Xin=[rand(100,2);3+rand(100,2);7+rand(100,2);10+rand(100,2)];
// Находим кластеры
centers=subclust(Xin);
Результат выполнения примера представлен на рисунке 11.

Рисунок 4 – Результат выполнения функции subclust
Функция inwichclust
Данная функция предназначена для нахождения ассоциированного с точкой кластера.
Прототип функции:
po=inwichclust(X,centers)
Параметры:
-
X: матрица вещественных чисел. Точки с данными. -
Centers: матрица вещественных чисел. Центры кластеров. -
Po: матрица целых чисел. Ассоциированный кластер для каждой точки.
Функция inwichclust возвращает позицию ближайшего центра кластера для каждой пары точек из Х.
Пример:
// Сгенерируем 10 точек с центром (1,1) (2,2) и (5,5)
X=[1+rand(10,2);2+rand(10,2);5+rand(10,2)];
centers=subclust(X);
po=inwichclust(X,centers);

Рисунок 5 – Результат выполнения функции inwichclust
Практическое выполнение нечеткой кластеризации в SciLab
Решим задачу нечеткой кластеризации на примере реальных данных. В качестве исходных данных возьмем результаты агрохимического исследования почвы (рисунок 6).

Рисунок 6 – Результаты агрохимического исследования почвы.
Для поиска кластеров будем пользоваться функций fcmeans. Для начала произведем алгоритм нечеткой кластеризации для значений калия в почве.
Результаты выполнения нечеткой кластеризации представлены на рисунке 7.

Рисунок 7 – Результат выполнения нечеткой кластеризации для данных о содержании калия в почве
Исходя из графика видно, что образуется три кластера, значения каждого из которых соответственно равны: 11.69, 18.28 и 6.92.
Произведем аналогичный анализ для данных о содержании фосфора в почве. Результат выполнения представлен на рисунке 8.

Рисунок 8 – Результат выполнения нечеткой кластеризации для данных о содержании фосфора в почве
Исходя из графика видно, что образуется три кластера, значения каждого из которых соответственно равны: 21.38, 14.13 и 8.24.
Листинг программы:
clear()
clc()
//Путь к файлу с данными
filename = fullfile("C:","\Scilab","\Fosfor.txt");
//Считываем данные из файла
Xin=fscanfMat(filename);
//Запоминаем максимальное, минимальное значение в файлах и его длину
//это необходимо для более удобного отображения графика
mmax=max(Xin);
mmin=min(Xin);
len=length(Xin);
//выполняем нечеткую кластеризацию
[centers,U,ofun,ofunk]=fcmeans(Xin,3,2);
// выводим информацию
scf();
clf();
subplot(2,2,1);
plot(Xin(:,1),'black+');
a=gca();
a.data_bounds=[0,mmin-0.05;len,mmax];
xgrid(5, 1, 7);
xtitle("Входные точки","Индекс","Значение");
subplot(2,2,3);
plot(centers(:,1),'black*');
a=gca();
a.data_bounds=[0,-1;length(centers)+0.01,max(centers(:,1))+2];
xgrid(5, 1, 7)
xtitle("Центры кластеров",'Номер кластера',"Значение");
subplot(2,2,2);
plot(ofunk);
xtitle("Значение ЦФ в каждой итерации","k","ofun");
Заключение
В результате проведенного исследования мы выяснили задачи и цели кластеризации, в частности нечеткой кластеризации. Познакомились с системой компьютерной математики SciLab и рассмотрели способы решения задач нечеткой кластеризации на основе реальных данных.
В заключение можно сказать, что нечеткая кластеризация позволяет давать ответы на вопросы, когда данные описывают объекты или процессы в условиях неопределенности. Например, когда требуется оценить, болезненность цвета лица пациента, кредитоспособность заемщика, качество изделия и др..
Список литературы
-
Нечеткие интеллектуальные системы в среде SciLAB: методические указания к лабораторным работам / сост. Н. Г. Ярушкина, Н. Н. Ястребова, А. В. Чекина. – Ульяновск : УлГТУ, 2009. – 28 с. -
Метод адаптивной нечеткой кластеризации на основе субъективных оценок для управления качеством производства светотехнических изделий: диссертация // Мальков, Александр Анатольевич. 2009г. – 248 с. URL: https://www.dissercat.com/content/metod-adaptivnoi-nechetkoi-klasterizatsii-na-osnove-subektivnykh-otsenok-dlya-upravleniya-ka -
Справка SciLab: электронный ресурс. URL: https://help.scilab.org/