Файл: Расчет токов ветвей электрической цепи методом контурных токов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 62
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное автономное образовательное учреждение высшего образования
«РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ»
(РУДН)
Инженерная академия
Департамент механики и мехатроники
Курсовая работа по дисциплине:
«Электротехника и электроника»
на тему: «Расчет токов ветвей электрической цепи методом контурных токов»
Выполнила:
Самойлова Ольга Александровна
Группа:
ИУСбз-02-21
№ студ. билета:
1132210005
Проверил:
Дата:
Подпись:
МОСКВА
2022
Оглавление
Введение 3
Постановка задачи электротехники 3
Описание метода решения задачи 4
Описание схемы 7
Аналитическое решение задачи 8
Решение задачи в программе MicroCap 9.0 13
Оценка полученных результатов 15
Вывод 16
Введение
Постановка задачи электротехники
Целью курсовой работы является расчет токов, протекающих через элементы заданной схемы с применением метода контурных токов.
Для достижения цели курсовой работы требуется решение следующих задач:
-
Изучить порядок расчета электрических цепей методом контурных токов; -
Провести анализ электрической схемы; -
Провести аналитический расчет токов ветвей схемы методом контурных токов; -
Провести моделирование работы схемы в программе MicroCap 9.0; -
Сравнить результаты аналитического расчета и моделирования; -
Сделать выводы по работе.
Описание метода решения задачи
Ветвью электрической цепи называют последовательное соединение источников и приёмников электрической энергии, имеющее два зажима (концевых точек) для присоединения её к другим участкам цепи. Все элементы ветви связаны между собой простыми узлами. Число элементов в ветви может быть любым. Перед анализом цепи целесообразно её упростить, заменив каждую ветвь её каноническим аналогом, включающим минимальный набор элементов.
Замена группы однотипных элементов на эквивалентные не зависит от того, в каком месте ветви расположен тот или иной элемент, так как величина тока одинакова в любом месте расположения измерительного прибора (амперметра).
Пусть электрическая цепь в только ветви первого типа, а ветви с источниками тока отсутствуют. Тогда число независимых контуров и, следовательно, контурных токов определится формулой:
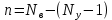
Система формализованных уравнений принимает вид:
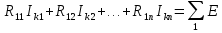
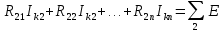
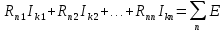
В этой системе:
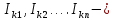 контурные токи, число которых совпадает с числом независимых контуров – n. Обходы по контурам совпадают с направлением действия контурных токов, которые указываются произвольно. Каждый ток замыкается в собственном контуре (i = 1, 2, ... n).
контурные токи, число которых совпадает с числом независимых контуров – n. Обходы по контурам совпадают с направлением действия контурных токов, которые указываются произвольно. Каждый ток замыкается в собственном контуре (i = 1, 2, ... n).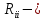 собственное сопротивление i‐го контура. Складывается из всех сопротивлений ветвей, принадлежащих этому контуру. В систему записывается всегда со знаком плюс.
собственное сопротивление i‐го контура. Складывается из всех сопротивлений ветвей, принадлежащих этому контуру. В систему записывается всегда со знаком плюс.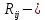 взаимное сопротивление i‐го и j-го контуров. Складывается из сопротивлений всех ветвей, которые лежат на границе этих контуров. В систему записывается со знаком плюс, если контурные токи в смежных ветвях совпадают по направлению, и со знаком минус, если токи направлены встречно. Если контура не имеют общих ветвей, то это сопротивление приравнивается нулю.
взаимное сопротивление i‐го и j-го контуров. Складывается из сопротивлений всех ветвей, которые лежат на границе этих контуров. В систему записывается со знаком плюс, если контурные токи в смежных ветвях совпадают по направлению, и со знаком минус, если токи направлены встречно. Если контура не имеют общих ветвей, то это сопротивление приравнивается нулю.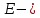 контурная ЭДС i‐го контура. Складывается алгебраически из всех ЭДС, принадлежащих i-тому контуру. Знаки слагаемых согласуются с направлением действия контурного тока.
контурная ЭДС i‐го контура. Складывается алгебраически из всех ЭДС, принадлежащих i-тому контуру. Знаки слагаемых согласуются с направлением действия контурного тока.Решается система уравнений, определяются контурные токи. Затем рассчитываются токи ветвей как алгебраическая сумма контурных токов, протекающих в каждой ветви.
Метод контурных токов применим и для электрических цепей, состоящих как из ветвей первого, так и второго типа. В учебной литературе этот вопрос либо не рассматривается
, либо рекомендуется пользоваться эквивалентным преобразованием ветвей второго типа в ветви первого типа. Однако любое преобразование исходной цепи не всегда возможно, да и требует обратного возврата к исходной цепи, что значительно увеличивает время анализа. Поэтому эквивалентными преобразованиями следует пользоваться в крайних случаях. Уточним понятие независимого контура, под которым ранее считался контур, образованный ветвями только первого типа. Токи ветвей второго типа учитывались в уравнениях, которые составлялись по первому закону Кирхгофа, и через эти уравнения оказывалось их влияние на распределение токов в цепи. В методе контурных токов число уравнений в системе меньше, чем число неизвестных токов, и, следовательно, есть необходимость дополнительно включить информацию об источниках тока в эту систему. Независимыми контурами в методе контурных токов будем считать контура, которые образованы как ветвями первого, так и второго типа. Выбор контуров следует начинать с ветвей первого типа, затем – второго, и так, чтобы в каждой ветви второго типа протекало бы не больше одного контурного тока. Если таких токов окажется два и больше, то будет неопределённость: (Какой же ток на самом деле будет протекать в данной ветви второго типа?). Первоначально систему уравнений можно записать по типу вышерассмотренной системы, т.е. по числу независимых контуров. Но некоторые контурные токи уже известны – это токи ветвей с уже заданными источниками тока. Поэтому каждое уравнение, которое записано для контура, управляемого ветвью второго типа, следует переписать как простое равенство: Iki =Ji. Если слагаемые с известными токами перенести в правую часть системы уравнений, то порядок системы уравнений уменьшится, и задача упростится.
Описание схемы
Согласно варианту на курсовую работу, необходимо рассчитать токи в ветвях схемы, представленной на рис.1.1.
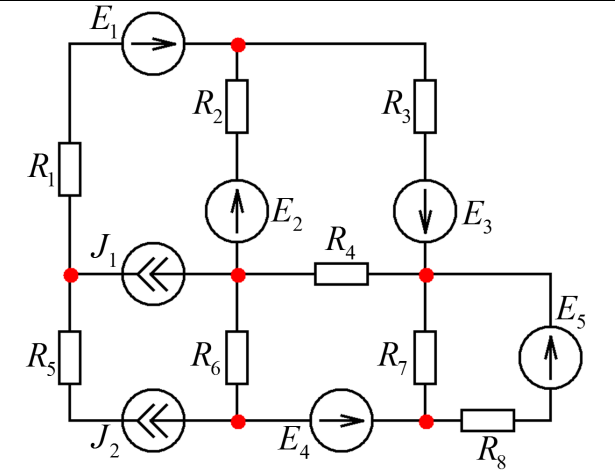 |
| Рис. 1.1 Схема для расчета |
В состав схемы входят:
-
Идеальные источники тока (J1, J2); -
Идеальные источники напряжения (E1, E2, E3, E4, E5); -
Резисторы (R1, R2, R3, R4, R5, R6, R7, R8).
Значения всех элементов представлены в таблице 1.
Таблица 1
| Вариант 1 | R1 | R2 | R3 | R4 | R5 |
| 2 Ом | 4 Ом | 6 Ом | 3 Ом | 5 Ом | |
| R6 | R7 | R8 | E1 | E2 | |
| 2 Ом | 10 Ом | 4 Ом | 5 В | 15 В | |
| E3 | E4 | E5 | J1 | J2 | |
| 24 В | 12 В | 8 В | 3 А | 4 А |
Аналитическое решение задачи
Сначала определим контура, а также зададим направления токов в ветвях (рис. 2.1).
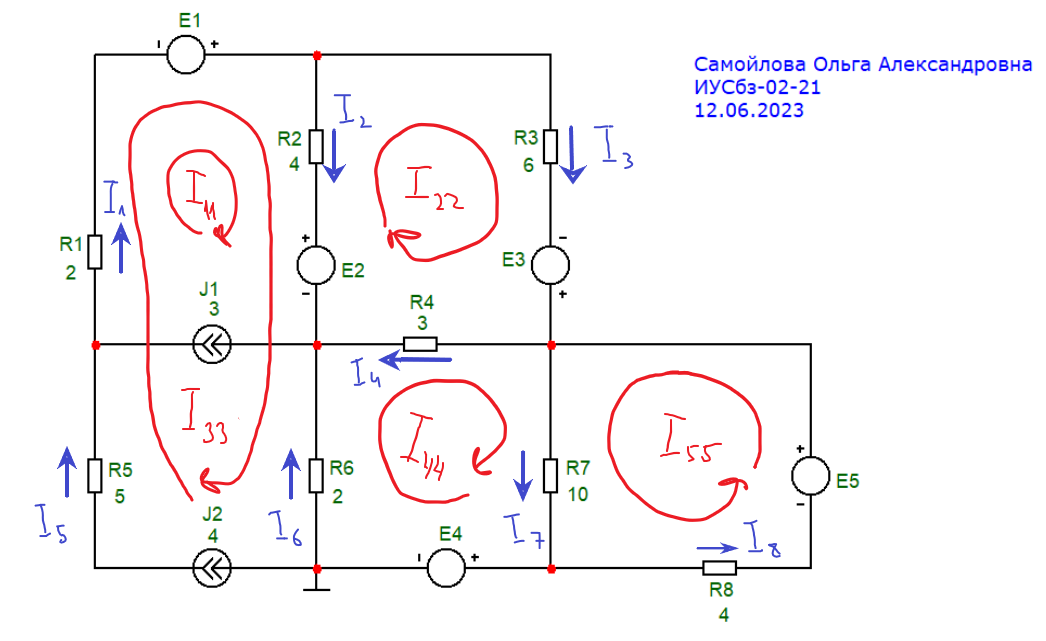 |
| Рис. 2.1 Определение контуров, направлений контурных токов и токов в ветвях |
Рассчитаем собственные сопротивления контуров, взаимные сопротивления контуров и контурные ЭДС в таблице 2.
Таблица 2
| Собственные сопротивления контуров: | ||
| R22 | 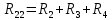 | 13 Ом |
| R44 | 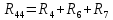 | 15 Ом |
| R55 | 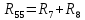 | 14 Ом |
| Взаимные сопротивления контуров | ||
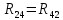 | 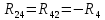 | -3 Ом |
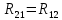 | 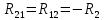 | -4 Ом |
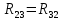 | 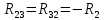 | -4 Ом |
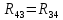 | 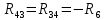 | -2 Ом |
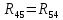 | 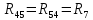 | 10 Ом |
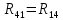 | 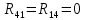 | 0 Ом |
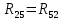 |  | 0 Ом |
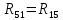 | 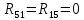 | 0 Ом |
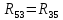 | 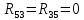 | 0 Ом |
| Контурные ЭДС | ||
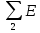 | 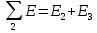 | 39 В |
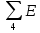 | 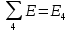 | -12 В |
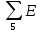 | 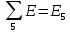 | 8 В |
Далее составим матрицу, учитывая, что в схеме находится 2 идеальных источника тока. Для них контурные токи Ik1=J1 и Ik2=J2.
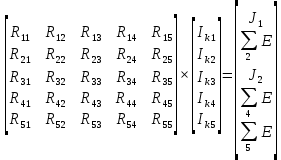
Подставим в матрицу наши значения.
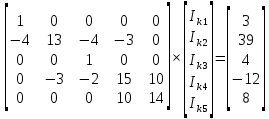
Далее будем решать матрицу и находить определители.
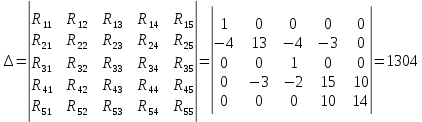
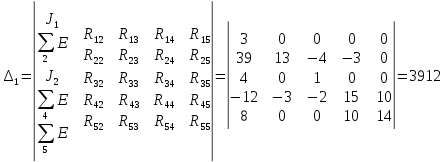
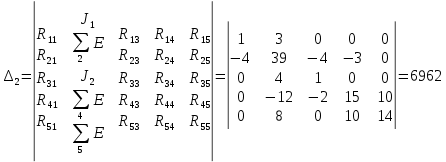
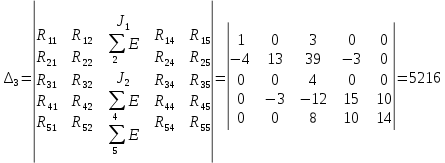
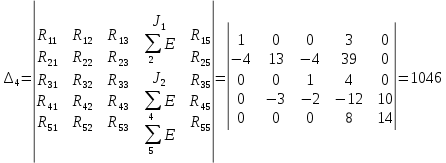
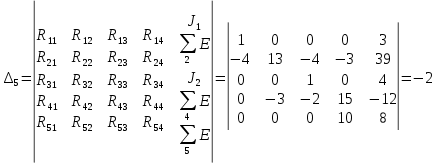
Получаем контурные токи.
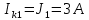
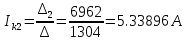
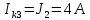
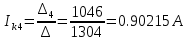
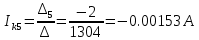
Записываем значения контурных токов в таблицу 3.
Таблица 3
| Контурные токи | |
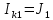 | 3 A |
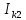 | 5.33896 А |
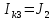 | 4 А |
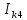 | 0.90215 А |
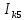 | -0.00153 А |
Находим значения действительных токов