Файл: Отчет о лабораторных работах по учебной дисциплине Основы алгоритмизации и программирования олр 090207. 09.docx

Д епартамент образования Ярославской области Государственное профессиональное образовательное автономное учреждение Ярославской области «ЯРОСЛАВСКИЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ им. Н.П. ПАСТУХОВА»
Отчет о лабораторных работах по учебной дисциплине «Основы алгоритмизации и программирования»
ОЛР 090207.09
	Студент _____________ В.О. Терентьева «____»______________2022____г.
	Преподаватель _____________ Е.С. Шестёркина «____»______________20____г.
2022

Содержание

Практическая работа № 1,2.

Тема: Составление блок-схем линейных и разветвляющихся и циклических алгоритмов.

Цель: Научиться составлять блок-схемы линейных, разветвляющих и циклических алгоритмов

1. 
   Выполнить этапы 1-3 для решения задач.
   
2. 
   Построить алгоритм, используя программу MS Visio.
   
3. 
   Для циклических алгоритмов построить трассировочную таблицу на одном из тестовых наборов
   

Теоретическая часть

Этапы решения задачи на ЭВМ:

1. Постановка задачи (должно быть четко сформулировано, что дано и что требуется найти, определить полный набор исходных данных).

---

2. Формализация задачи (задача переводится на язык математических формул, уравнений, отношений).

3. Построение алгоритма.

4. Составление программы на языке программирования.

5. Отладка и тестирование программы.

6. Проведение расчетов и анализ полученных результатов.

Базовые алгоритмические структуры:

• 
  следование,
  
• 
  ветвление,
  
• 
  повторение.
  

На рисунке 1 представлены условные обозначения, используемые при записи алгоритма с помощью блок-схем, для указанных структур: для следования, ветвления, выбора (частный случай ветвления), для повторения (цикл с предусловием, цикл с постусловием, цикл с параметром).







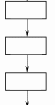
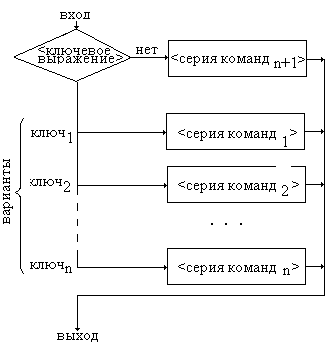
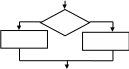
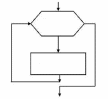
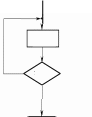
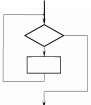
Рисунок 1. Условные обозначения, используемые при записи алгоритма с помощью блок-схем.

Практическая часть

Вариант №24

Задача 1

Определить, сколько времени в минутах затратит школьник на дорогу из школы до стадиона, если известна длина этого расстояния S км и средняя скорость движения школьника v км/ч?

1. 
   Вход: S (вещественное число, расстояние от школы до стадиона); v (вещественное число, средняя скорость движения школьника). Ввод с клавиатуры.
   

Выход: t (вещественное число, время, затраченное на дорогу в минутах) или t1 (вещественное число, время, затраченное на дорогу в часах) и t2 (вещественное число, время, затраченное на дорогу в минутах).

Вывод на экран

2. 
   Формализация
   

S – км

v – км/ч

t=S/v

t, S, v>0 – число

t, S, v<0 – нет решений

v=0 – нет решений

t = t*60 – в минутах; если t>60, то t1=t/60 (часов), t2=t-t1*60 (минут)

3. 
   Блок-схема
   

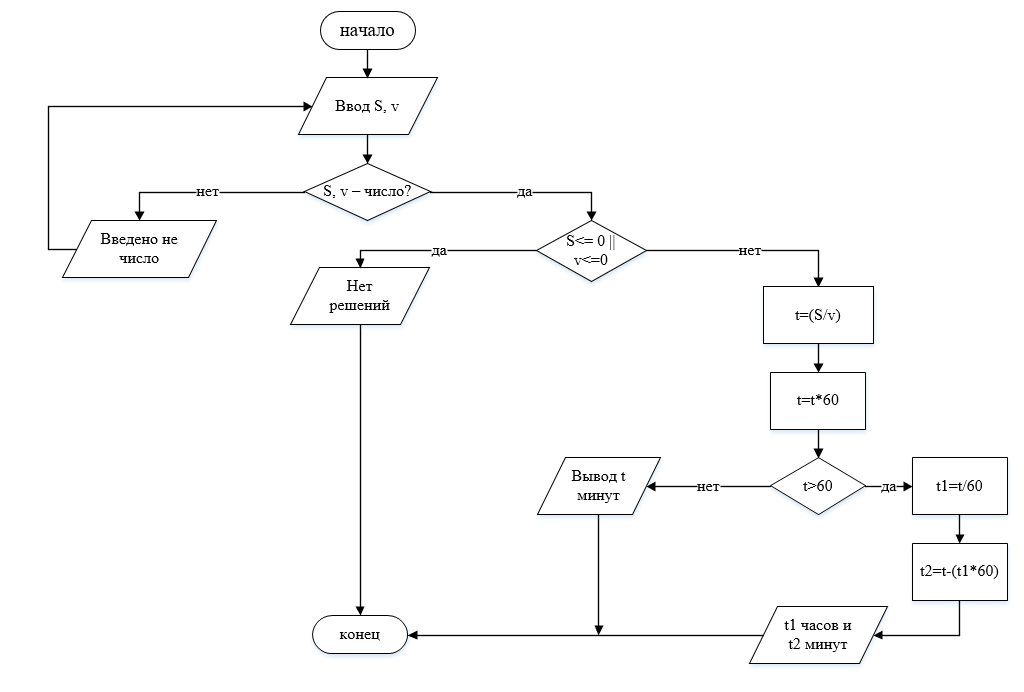На рисунке 2 представлена блок-схема для вычисления времени, которое затратит школьник на путь от школы до стадиона.
Рисунок 2. Блок-схема для вычисления времени, которое затратит школьник на путь от школы до стадиона.

---

4. 
   Программа
   

На рисунке 3 представлена программа для определения, затраченного времени (в минутах) школьником на дорогу из школы до стадиона.


Рисунок 3. Программа для 1 задачи

5. 
   Тестирование
   

В таблице 1 представлены тестовые наборы для проверки работоспособности программы, выполненной в предыдущем шаге.

Таблица 1. Тестовые наборы для 1 задачи

N	Вход		Выход				результат
	S	v	t	t1	t2	сообщение
нормальное	11	5	-	2	12	-	2 часа 12 минут
нормальное	4	3	-	1	20	-	1 час 20 минут
нормальное	0,5	5	6	-	-	-	6 минут
экстремальное	3	0	-	-	-	Нет решений	-
экстремальное	1	-2	-	-	-	Нет решений	-
экстремальное	-3	2	-	-	-	Нет решений	-
исключительное	?	1	-	-	-	Введено не число	-
исключительное	3	ъ	-	-	-	Введено не число	-

На рисунках 6-8 представлены скриншоты окна консоли с работающей программой со значениями из таблицы тестирования.

---

Рисунок 4. Окно консоли с нормальными значениями из таблицы тестирования



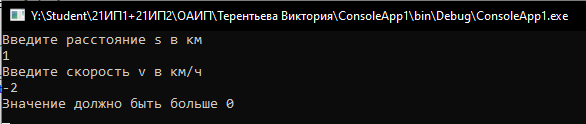
Рисунок 5. Окно консоли с экстремальными значениями из таблицы тестирования



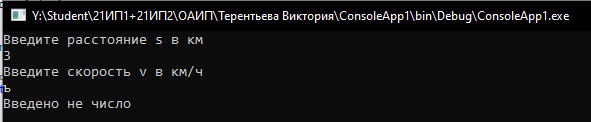
Рисунок 6. Окно консоли с исключительными значениями из таблицы тестирования

6. 
   Вывод
   

Мы написали корректно работающую программу для задачи, по поиску времени, которое школьник затратил на путь от школы до стадиона.

Задача 2

Определить стоимость заказа печати фотографий. Исходные данные для расчета— размер (9x12, 12x15 или 18x24) и количество фотографий. Если количество фотографий больше 20, то предоставляется скидка 10%.

1. 
   Вход: 1 (фотография размером 9х12), 2 (фотография размером 12х15), 3 (фотография размером 18х24); t (вещественное число, количество фотографий) вводится с клавиатуры.
   

Выход: x (вещественное число, стоимость заказа).

Вывод на экран

2. 
   Формализация
   

Если а1=> x=14, a2=>x=16, a3=>x=20

t>0 - число

t<0 – нет решений

t=0 – нет решений

Sum=t*x, если t>20, то Sum=sum-0.1*sum

3. 
   Блок-схема
   

На рисунке 3 представлена блок-схема, для определения стоимости фотографии.

4. 
   
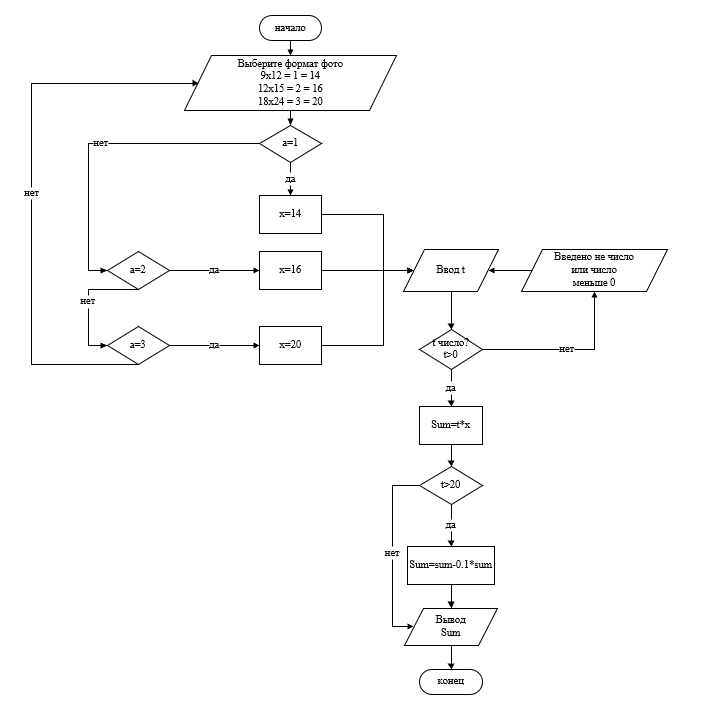
   Рисунок 7. Блок-схема для вычисления стоимости фотографии.
   Программа
   

5. 
   Тестирование
   

В таблице 2 представлены тестовые наборы для проверки работоспособности программы, выполненной в предыдущем шаге.
Таблица 2. Тестовые наборы для 2 задачи

N	Вход				Выход		Результат
	1	2	3	t	x	сообщение
нормальное	14	16	20	4	56	-	56
нормальное	14	16	20	20	320	-	320
нормальное	14	16	20	23	414	-	414
экстремальное	14	16	20	0	-	Нет решений	-
экстремальное	14	16	20	-6	-	Нет решений	-
исключительное	14	16	20	T	-	Введено не число	-
исключительное	14	16	20	^	-	Введено не число	-

---

6. 
   Вывод
   

Мы написали корректно работающую программу для задачи, по определению стоимости заказа печати фотографии.

Задача 3

Вывести таблицу значений функции y= 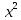+lnx с шагом h на отрезке [a,b] (h,a,b вводятся с клавиатуры)

1. 
   Вход: х (вещественное число). h (вещественное число, шаг на отрезке), a (вещественное число, начало отрезка) b (вещественное число, конец отрезка)> ввод с клавиатуры.
   

Выход: таблица значений функции y=x2 +lnx – пары [a,b]. Вывод на экран.

2. 
   Формализация
   

y=x2 +lnx – возрастающая функция

[a,b] – отрезок

a – начало, b – конец.

a, b, h – числа

a<=b

3. 
   Блок-схема
   

На рисунке 4 представлена блок схема, для вывода таблицы значений функции y= 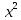+lnx с шагом h на отрезке [a,b].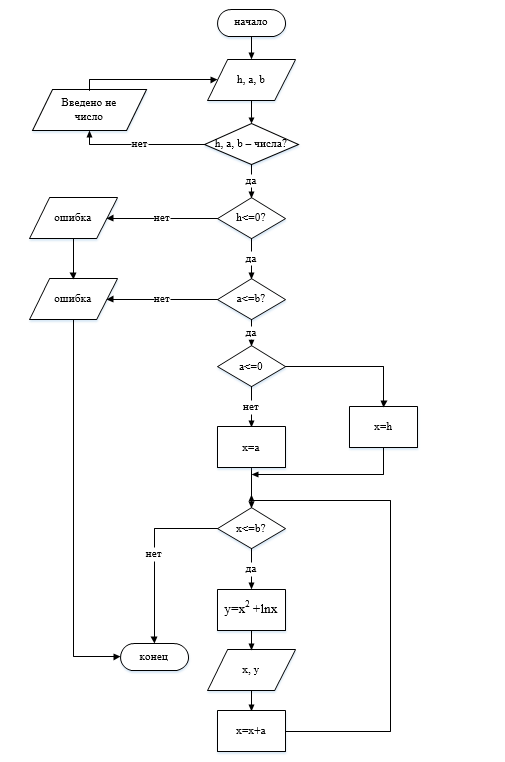



Рисунок 8. Блок-схема для вывода таблицы значений функции y=х^2+lnx с шагом h на отрезке [a,b].

4. 
   Программа
   

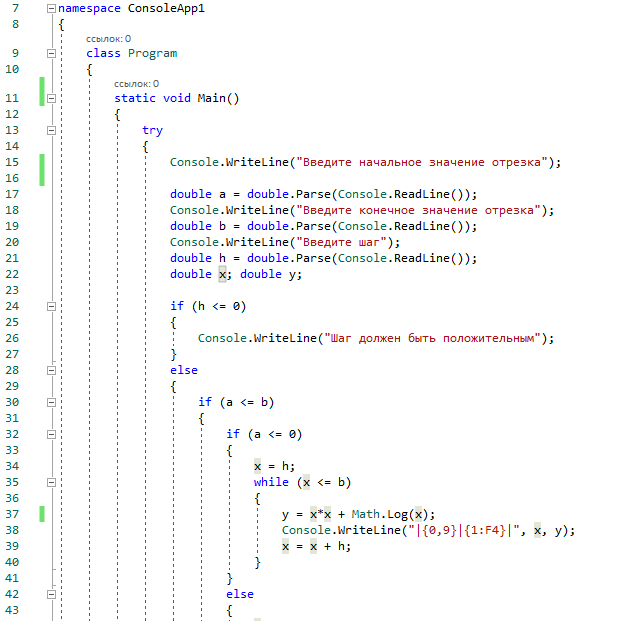
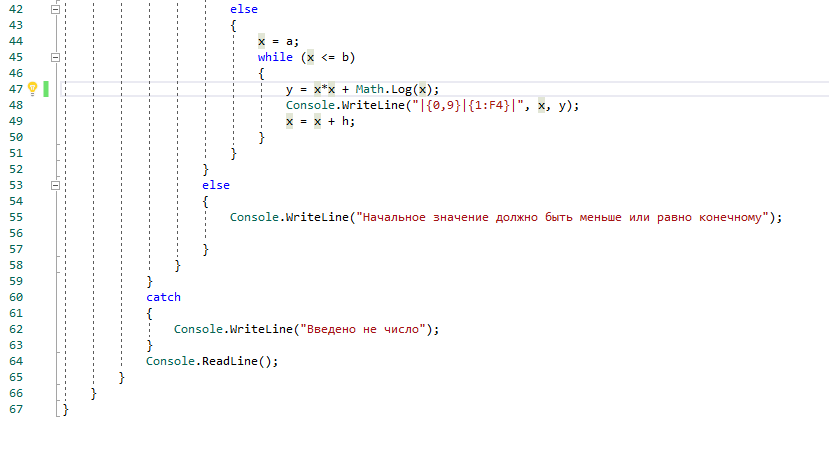
На рисунке 5 представлены скриншоты программы, для вывода таблицы значений функции y=х^2+lnx с шагом h на отрезке [a,b].

5. 
   Тестирование
   

В таблице 3 представлены тестовые наборы для проверки работоспособности программы, выполненной в предыдущем шаге.

Таблица 3. Тестовые наборы для 3 задания

N	Вход			Выход				Результат
	h	a	b		x	y	сообщение
нормальное	0.5	2	6		2 2,5 3 3,5 4 4,5 5 5,5 6	4,6931 5,9163 7,0986 8,2528 9,3863 10,5041 11,6094 12,7047 13,7918	-		| 2|4,6931| | 2,5|5,9163| | 3|7,0986| | 3,5|8,2528| | 4|9,3863| | 4,5|10,5041| | 5|11,6094| | 5,5|12,7047| | 6|13,7918|
экстремальное	1	-2	9		1 2 3 4 5 6 7 8 9	1,0000 4,6931 10,0986 17,3863 26,6094 37,7918 50,9459 66,0794 83,1972	-		| 1|1,0000| | 2|4,6931| | 3|10,0986| | 4|17,3863| | 5|26,6094| | 6|37,7918| | 7|50,9459| | 8|66,0794| | 9|83,1972|
экстремальное	-1	-2	2		-	-	Шаг должен быть положительным		-
исключительное	!	2	4		-	-	Введено не число		-
исключительное	1	ъ	3		-	-	Введено не число		-

---