Файл: Методические рекомендации по выполнению домашней контрольной работы 1 методические рекомендации по выполнению домашней контрольной работы 2.docx

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по выполнению домашней контрольной работы по дисциплине

Высшая математика

Направленность (профиль) образовательной программы

«Менеджмент в электроэнергетике и электротехнике»

Направление подготовки

13.03.02 Электроэнергетика и электротехника
Для обучающихся заочной формы обучения

Челябинск, 2019
СОДЕРЖАНИЕ

ВВЕДЕНИЕ

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ №1

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ №2

ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ №1

ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ №2

РЕКОМЕНДУЕМЫЙ СПИСОК ЛИТЕРАТУРЫ

ВВедение
Курс дисциплины «Высшая математика» является фундаментом дальнейшего образования инженера, имеющим важное значение не только для изучения общетехнических дисциплин, но и для специальных дисциплин в особенности.
Изучив дисциплину «Высшая математика» студент должен:
- Ознакомиться с основами линейной алгебры, высшей алгебры, векторной алгебры, аналитической геометрии, дифференциальной геометрии, кривых и поверхностей, элементами топологии.
- Изучить основы математического анализа, дифференциальное исчисление функций одного и нескольких переменных, изучить неопределенные и определенные интегралы, кратные интегралы, ознакомиться с элементами дискретного анализа.
- Знать основные типы дифференциальных и разностных уравнений и методы их решения.
- Знать и уметь использовать на практике признаки сходимости числовых и функциональных рядов.
- Иметь представление о функциях комплексного переменного и элементах теории поля.
- Ознакомиться с основами вариационного исчисления и оптимального управления.
- Знать важнейшие понятия теории вероятностей и математической статистики.

---

- Иметь представление о моделях случайных процессов и элементах теории массового обслуживания.
- Иметь представление о временных рядах, математическом моделировании.

В процессе выполнения контрольной работы у обучающихся формируются компетенции, указанные в рабочей программе дисциплины «Высшая математика»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ №1
Раздел 1 Линейная и векторная алгебра. Аналитическая геометрия

Матрицы и определители

Определение матрицы. Виды матриц. Транспонирование матриц. Алгебраические операции над матрицами. Определители второго, третьего порядков и матрицы n-го порядка. Теорема Лапласа. Присоединенная и обратная матрицы. Алгоритм вычисления обратной матрицы. Ранг матрицы как наивысший порядок ее миноров, отличных от нуля. Вычисление ранга матрицы с помощью элементарных преобразований. Линейная комбинация, линейная зависимость и независимость строк (столбцов) матрицы. Теорема о ранге матрицы — максимальном числе ее линейно независимых строк (столбцов). (1, гл.1, § 1.1-1.6; с.9-35); (2, гл.1).

Надо хорошо уяснить, что матрица — это прямоугольная таблица, составленная из mn чисел, расположенных в m строках и nстолбцах. Необходимо знать, как устанавливаются размеры матрицы и ее порядок, уметь выполнять транспонирование матриц, алгебраические операции над ними (умножение матрицы на число, сложение, вычитание, умножение матриц).

Необходимо усвоить следующее: строки обозначаются индексом ”i”, столбцы индексом ”j”. Поэтому любой элемент матрицы можно обозначить a_ij. Это означает, что элемент a_ij находится в i-ой строке и в j-ом столбце. Например, a₁₁ – элемент первой строки и первого столбца; a₂₃–элемент второй строки и третьего столбца. Индекс с «i» растет всегда «вниз», а индекс «j» – растет вправо.

Размер матрицы m х n означает, что конечные величины i и j равны соответственно m и n, т.е. i_кон=m, j_кон=n.

При вычислении определителей необходимо отметить, что определитель есть число и вычисляется по определенным правилам. Необходимо рассмотреть правило вычисления определителей второго порядка и правило треугольника или правило Сарруса для вычисления определителей третьего порядка.

---

В качестве универсального метода вычисления определителей необходимо рекомендовать вычисление на основе теоремы Лапласа.

Для этого нужно знать определение минора (вычисление), определение алгебраического дополнения A_ij=(-1)^i+jM_ij и саму теорему Лапласа. (1, пример 9, с. 25, с. 26).

Мало того, нужно обратить внимание и на то, что определители порядка больше трех вычисляются с помощью теоремы Лапласа.

Относительные трудности возникают при усвоении операции умножения матриц. Необходимо твердо усвоить формальное правило умножения ( 1, с. 12 – 13) и связанное с ним условие существования произведения АВ матриц А и В:число столбцов матрицы А должно быть равно числу строк матрицы В. Одна из особенностей операции умножения состоит в том, что произведение матриц в общем случае не коммутативно, т.е. АВ  ВА. Даже если А и В – квадратные матрицы, в общем случае АВ  ВА, в чем нетрудно убедиться на любом частном примере. Другая особенность произведения матриц состоит в том, что произведение двух ненулевых матриц может оказаться нулевой матрицей.

Например, можно легко показать, что произведение матриц есть нулевая матрица (сравните: во множестве действительных чисел произведение равно нулю тогда, когда хотя бы один из сомножителей равен нулю).

=

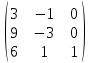
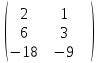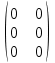
Нужно знать определение присоединенной и обратной матриц, уметь их вычислять, знать, что для существования матрицы А^-1 , обратной матрице А, необходимо и достаточно, чтобы матрица А была невырожденной (неособенной). Проверить правильность вычисления обратной матрицы можно, составив произведение АА^-1или А^-1 А. Если оно является единичной матрицей Е, то, в соответствии с определением, матрица А ^-1 вычислена правильно.

Нужно уметь вычислять определители второго и третьего порядков (метод треугольника) и более высших порядков (1, пример 1.9, c.25, 26). При вычислении определителей нужно активно использовать свойства определителей 2,4,5,6,8. Теорему Лапласа нужно знать твердо и уметь ее использовать для практики.

---

Разобрать для усвоения материала по вычислению определителей задачи 1.19-1.21.

Вычисление обратной матрицы осуществлять по алгоритму, изложенному в (1). Нужно четко усвоить в алгоритме, что обратная к исходной матрице существует. После этого определяется транспонированная к исходной матрица. Именно для транспонированной матрицы А ищутся алгебраические дополнения A_ij.

Из алгебраических дополнений к транспонированной матрице составляется присоединенная (союзная) матрица.

Если известна союзная матрица 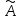и определитель исходной матрицы, то вычисляется обратная матрица

A^-1= / .

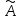Обратная матрица будет использоваться для решения систем линейных уравнений.

Для усвоения материала необходимо разобрать задачи (1, 1.15— 1.18, 1.22—1.29).

Пример: Найти матрицу С=ВААВ, если А= , В= .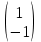

Решение:

Алгоритм решения:

1. 
   Находим матрицы В, А, транспонированные к матрицам А и В.
   

А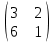= , В= .

2. 
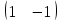   Находим произведение матриц:
   

ВА=  = .

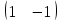
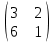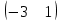Это возможно ибо число столбцов матрицы В равно числу строк матрицы А.

3. 
   Находим произведение матриц:
   

АВ= = .

4. 
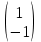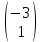   Находим произведение
   

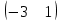
С=ВААВ= 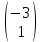= (10)

Ответ: C = (10)

Система линейных уравнений

Система n линейных уравнений с n переменными (общий вид). Матрица системы. Матричная форма записи системы. Совместные (определенные и неопределенные) и несовместные системы. Теорема Крамера о разрешимости системы

---

n линейных уравнений с n переменными (без доказательства). Решение системы: по формулам Крамера; с помощью обратной матрицы; методом Гауса. (1, гл. 2, §2.1—2.3,2.6; с. 38—47,53—56); (2, гл. 2).

При изучении материала темы следует освоить матричную форму записи заданной системы п линейных уравнений с п переменными и уметь переходить к этой форме от общего вида системы и наоборот. Необходимо знать и уметь объяснить, какие системы уравнений называются совместными (определенными и неопределенными) и несовместными. Надо твердо уяснить, что вопрос о разрешимости системы nлинейных уравнений с n переменными устанавливается с помощью теоремы Крамера (1, с. 41); решаются же такие системы различными способами: по формулам Крамера, с помощью обратной матрицы и методом Гаусса (см. примеры 2.1 – 2.3, 2.6, 2.7).

Наиболее важен для практики метод Гаусса, имеющий по сравнению с другими способами решения ряд достоинств: он менее трудоемок, позволяет однозначно установить, является ли данная система определенной, неопределенной или несовместной, а в случае совместности системы – определить число ее независимых уравнений и исключить «лишние».

В методе Гаусса нужно усвоить правило исключения неизвестных х₁, х₂, …, х_n-1. Сначала умножается первая строка на соответствующие коэффициенты. Цель – в первом столбце во всех строках кроме первой обеспечить нули путем прибавления первой строки, умноженной на коэффициенты, ко второй и последующим строкам.

Затем умножается вторая строка на соответствующие коэффициенты. Цель – обеспечить нули во втором столбце во всех строках кроме второй (a₂₂ 0) путем прибавления к третьей и последующим строкам второй строки, умноженной на необходимые коэффициенты и т.д.

Для первой строки это коэффициенты (-a₂₁/a₁₁;-a₃₁/a₁₁;…;-a_m1/a₁₁); для второй строки это коэффициенты (-a₃₂/a₂₂;-a₄₂/a₂₂;…;-a_m2/a₂₂).

Необходимо понять, что при прямом ходе решения системы уравнений методом Гаусса определяется неизвестное х_n. Затем при обратном ходе определяются х_n-1, х_n-2 и так до х₁.

Необходимо уяснить, что метод Гаусса менее трудоемок особенно при решении систем уравнений более четвертого порядка.

---