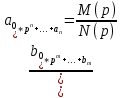ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 168
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 1.2 Функциональная схема замкнутой САР
Согласно определению, управляющее воздействие в замкнутой системе является функцией от рассогласования:
u(t)=F{ε(t)}
Достоинство: Регулируемая величина непрерывно контролируется.
По виду задающего воздействия g(t) замкнутые САР делятся на:
- системы стабилизации;
- системы программного регулирования;
- следящие системы.
В системах стабилизации заданное значение постоянно во времени:
g(t) = const
Пример: поддержание температуры, давления, концентрации и т.д. на заданном уровне.
В системах программного регулирования заданное значение изменяется во времени по строго определённой программе:
g(t) = f(t),
где f(t) – известная функция времени.
В следящих системах заданное значение изменяется произвольным, заранее неизвестным образом:
g(t) = η(t),
где η(t) – случайная, заранее неизвестная функция времени.
-
Разомкнутые системы – это системы, в которых отсутствует обратная связь и в которых задающие параметры воздействуют на регулируемые параметры объекта по разомкнутой цепи управления.
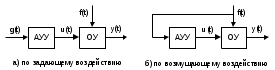
Рисунок 1.3 Функциональная схема разомкнутой САР
На рисунке 1.3а автоматическое управляющее устройство вырабатывает управляющее воздействие на основе информации о заданном значении регулируемой величины:
u(t)= F(g(t))
Недостаток: текущее значение управляемого параметра не контролируется.
На рисунке 1.3 б основой управления является метод компенсации, когда система непосредственно воздействует на причину динамических изменений регулируемого параметра, а именно на возмущение f(t), действующее на объект. АУУ использует информацию о текущем значении возмущающего воздействия и вырабатывает сигнал
, компенсирующий (устраняющий) возможные отклонения регулируемой величины:
u(t)= F(f(t))
Достоинством таких систем является высокое быстродействие, недостатком – низкая точность регулирования.
Пример: Рассмотрим принципы работы разомкнутой САР температуры нагревательной печи (рис. 1.4)
На рисунке 1.4 приняты следующие обозначения:
ОУ – объект управления (нагревательная печь);
БУ – блок усиления;
БС –блок соотношения;
ПЗУ – программируемое задающее устройство;
Д –датчик расхода топлива;
РО1 – регулирующий орган на линии подачи воздуха;
РО2- регулирующий орган на линии подачи топлива;
y1(t) – расход топлива;
y2(t) – расход воздуха;
u1(t) , u2(t) – управляющие воздействия;
g1(t) , g2(t) – задающие воздействия;
θ – температура в печи.
Задачи управления: 1) Температура в печи должна изменяться по заданному температурно – временному графику;
2) для обеспечения нормальных условий горения в печь должен подаваться воздух, в заданном соотношении от текущего значения расхода топлива.
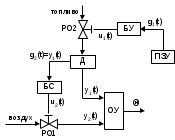
Рисунок 1.4 Схема разомкнутой САР температуры нагревательной печи.
Для решения первой задачи реализована программная САР по каналу «изменение расхода топлива – изменение температуры в печи». Здесь задающее воздействие g1(t) является известной функцией времени, которая определяется по температурно-временному графику печи.
Для решения второй задачи реализована следящая САР по каналу «изменение расхода воздуха – изменение температуры в печи». Здесь задающее воздействие g2(t) является неизвестной функцией времени, зависящей от соотношения текущего расхода топлива, измеряемого с помощью датчика (Д). Задание по этому каналу управления рассчитывается в блоке соотношения (БС).
§2 Математический аппарат исследования линейных систем автоматического регулирования
В §1 были рассмотрены основные функции элементов и систем автоматики, последовательность их включения в измерительную цепь.
При изучении динамических характеристик САР каждый элемент системы рассматривается
только с точки зрения динамики его работы, вне зависимости от функционального назначения.
Структурной схемой САР называется схема, где элементы показаны в виде прямоугольников (блоков), а направление сигналов указывается стрелками. Внутри блоков пишутся операторы преобразования входного сигнала в выходной. Функциональное назначение элементов не определяется.
На рисунке 3.1 приведён пример структурной схемы системы стабилизации.
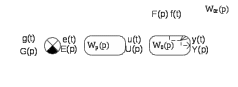
Рисунок 2.1 Структурная схема САР
Здесь Wp(р),Wo(р) - передаточные функции регулятора и объекта соответственно.
Динамика процессов управления, а также динамика работы элементов САР описывается дифференциальными уравнениями.
Линейной САР называется система, динамика работы которой описывается линейным дифференциальным уравнением.
Элементарным динамическим звеном называется часть САР, которая описывается дифференциальным уравнением не выше второго порядка.
Для упрощения решения дифференциальных уравнений используют преобразование Лапласа.
Преобразование Лапласа позволяет свести процесс решения линейного дифференциального уравнения к решению алгебраического уравнения при помощи специальных таблиц.
Таблица преобразований Лапласа
| f(t) | F(p) |
| (t) | 1 |
| 1(t) | 1/p |
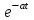 | 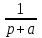 |
Таблица преобразований Лапласа
| f(t) | F(p) |
| (t) | 1 |
| 1(t) | 1/p |
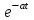 | 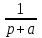 |
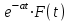 | F(p+a) |
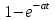 | 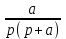 |
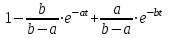 | 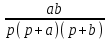 |
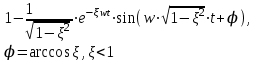 | 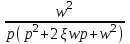 |
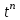 | 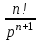 |
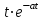 | 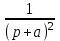 |
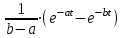 | 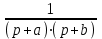 |
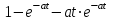 | 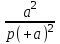 |
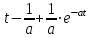 | 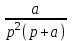 |
| f(n)(t), при н.н.у. | 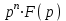 |
При использовании преобразования Лапласа производится операция перехода от функций времени f(t) (оригиналов) к функциям F(p) (изображениям ) комплексной переменной р.
Символически это записывается следующим образом:
L {f(t)} = F(p) – прямое преобразование;
L {F(p)} = f(t) - обратное преобразование.
Свойства преобразования Лапласа:
-
L{f1(t)+f2(t)+….+fn(t)} = F1(p)+F2(p)+…+Fn(p) -
L{A·f(t)} = A·F(p) , A=const -
L{f(t – τ)} = e · F(p).
Теоремы Лапласа о начальном и конечном значениях функции:
Начальное значение функции:
f(0) = lim f(t) = lim p·F(p)
t→0 p→∞
Конечное (установившееся) значение функции:
f(∞) = lim f(t) = lim p·F(p)
t→∞ p→0
§ 3 Передаточные функции линейных звеньев
Рассмотрим динамическое звено, которое находится под воздействием полезного сигнала х(t) и возмущение f(t).

Рисунок 1 Динамическое звено
Тогда его динамика описывается линейным неоднородным дифференциальным уравнением вида:
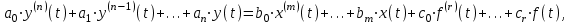 (1)
(1)преобразуем (1) по Лапласу при нулевых начальных условиях:
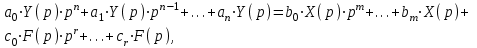 (2)
(2)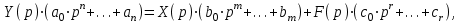 (3)
(3)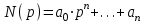
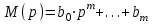
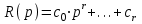
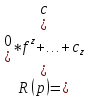 N(p), M(p), R(p) -операторные полиномы с постоянными коэффициентами;
N(p), M(p), R(p) -операторные полиномы с постоянными коэффициентами;Y(p),X(p),F(p)- изображение функций y(t),x(t),f(t) соответственно.
Передаточной функцией звена, по какому либо внешнему воздействию называется отношение изображения по Лапласу выходной величины к изображению по Лапласу рассматриваемого воздействия, при этом все другие внешние воздействия полагаются равными нулю.
Из определения следует, что для любого звена с одной выходной величиной число передаточных функций равно числу внешних воздействий.
Тогда для рисунка1 передаточная функция звена по полезному сигналу, при F(p)=0:
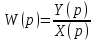 =
=