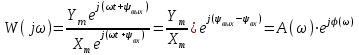ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 163
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§ 6. Передаточные функции линейных систем.
Рассмотрим линейную систему, находящуюся под влиянием задающего g(t) и возмущающегоf(t) воздействий (рис 6.1).

Рисунок 6.1 Структурная схема САР.
Передаточная функция регулятора:
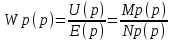
ПФ объекта по регулирующему воздействию:
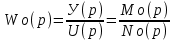
ПФ - ия объекта по возмущающему воздействию:
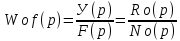
Операторное уравнение динамики объекта:
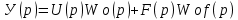 (1)
(1)
С учетом 1 структурная схема (рисунок 6.1) может быть представлена в виде (рис. 6.2).
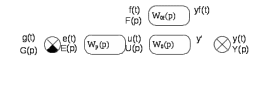
Рисунок 6.2 Упрощённая структурная схема
Если разорвать главную обратную связь и положить F(р)=0, то получим ПФ разомкнутой системы по задающему воздействию:
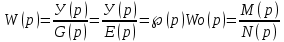
При этом структурная схема ( рис 6.2) упрощается (рис 6.3).
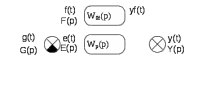
Рисунок 6.3 Структурная схема САР
Если разорвать главную обратную связь, то при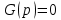 , получим ПФ разомкнутой системы по возмущающему воздействию:
, получим ПФ разомкнутой системы по возмущающему воздействию:
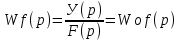
Рассмотрим теперь замкнутую систему (рисунок 6.3).
Передаточная функция замкнутой системы по задающему воздействию(при F(p)=0):
Ф(p)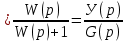
Учитывая, что
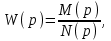
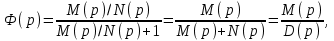
где N(p)- характеристический полином разомкнутой системы;
D(p)- характеристический полином замкнутой системы.
Рассмотрим возможные ПФ замкнутой системы. На основе схемы (рис. 6.3) составим сигнальный граф, где отобразим параметры системы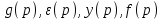 .
.
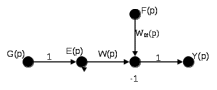
Рисунок 6.4 Сигнальный граф САР
При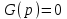
, получим ПФ- замкнутой системы по возмущающему воздействию:
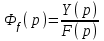 .
.
По формуле Мэзона имеем:
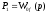 ;
;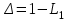 ;
; 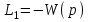 ;
;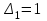 .
.
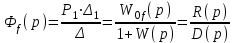 .
.
По полученным ПФ можно записать операторное уравнение относительно регулируемой величины:
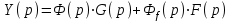 .
.
Если в качестве выходной величины рассматривать сигнал ошибки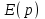 , а в качестве входной - сигнал задающего воздействия
, а в качестве входной - сигнал задающего воздействия 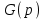 получим передаточную функцию замкнутой системы по ошибке от задающего воздействия.
получим передаточную функцию замкнутой системы по ошибке от задающего воздействия.
Из рисунка 6.4 следует:
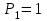 ;
; 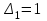 ;
; 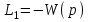
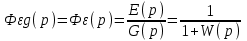 .
.
Найдем связь между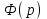 и
и 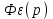 :
:
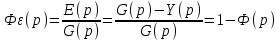 .
.
Учитывая, что возмущение также влияет на отклонение регулируемой величины, а, следовательно, и на сигнал ошибки, то определим ПФ замкнутой системы по ошибке от возмущающего воздействия:
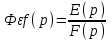 .
.
Из рисунка 6.4:
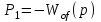 ;
; 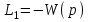 ;
; 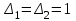
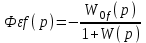 .
.
Таким образом, результирующая ошибка системы имеет две составляющие:
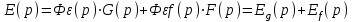 .
.
§7 Временные характеристики линейных звеньев
В реальных условиях входные сигналы имеют произвольный характер. Для исследования динамических свойств звеньев (систем) следует выбирать такие типовые сигналы, которые по возможности наиболее близко отражали бы наиболее существенные особенности реальных сигналов. Кроме того, для сравнения отдельных элементов и систем между собой их также следует подвергать однотипным воздействиям. К числу наиболее часто применяемых типовых сигналов относятся:
- единичная ступенчатая функция 1(t);
- единичная импульсная функция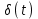 ;
;
- гармоническая функция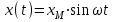 .
.
Временной характеристикой звена (системы) по какому-либо внешнему воздействию называют закон изменения выходной величины звена при изменении внешнего воздействия по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое (нулевые начальные условия).
1. Реакцию звена на воздействия в виде единичной ступенчатой функции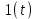 при нулевых начальных условиях называют переходной функцией
при нулевых начальных условиях называют переходной функцией 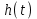 (рис. 7.1).
(рис. 7.1).
Графическое изображение переходной функции называют переходной характеристикой.











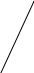


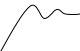


t
h(t)
1
0
t
x

Рисунок 7.1 Переходные характеристики линейных систем
Единичная ступенчатая функция определяется следующими условиями:
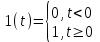 .
.
Согласно определению ПФ изображение выходного сигнала:
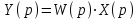 .
.
Учитывая, что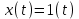
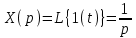 ,
,
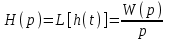 ,
,
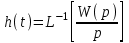 .
.
2. Реакция звена на воздействие в виде единичной импульсной функции при нулевых начальных условиях называется весовой или импульсной переходной функцией
при нулевых начальных условиях называется весовой или импульсной переходной функцией 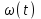 (рис 7.2).
(рис 7.2).
Графическое изображение функции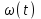 называется импульсной переходной характеристикой.
называется импульсной переходной характеристикой.

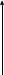

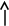








0
t
ω(t)
-δ(t)
t
x(t)
Рисунок 7.2 Импульсная переходная характеристика
Единичная импульсная функция или дельта-функция представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 7.2а).
представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 7.2а).
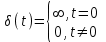 ;
;
Математически дельта - функцию можно представить как производную от единичной ступенчатой функции:
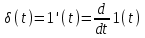 ,
,
отсюда следует
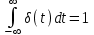
Учитывая, что входной сигнал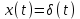 или
или 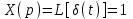 ,
,
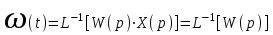
Переходная и импульсная
и импульсная 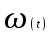 связаны соотношением:
связаны соотношением:
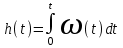 или
или 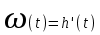
Обе временные характеристики и
и 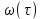 являются динамическими характеристиками и также полностью описывают свойства звена как ДУ и ПФ.
являются динамическими характеристиками и также полностью описывают свойства звена как ДУ и ПФ.

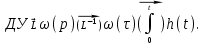
§8 Частотные характеристики линейных систем
При подаче на вход линейного звена гармонического воздействия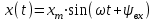 на выходе этого звена в установившемся режиме также будет получена гармоническая функция
на выходе этого звена в установившемся режиме также будет получена гармоническая функция 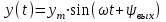 той же частоты
той же частоты 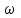 , но отличающаяся от входной по амплитуде и по фазе (рис. 8.1)
, но отличающаяся от входной по амплитуде и по фазе (рис. 8.1)

Рисунок 8.1 Гармонические сигналы
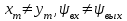
Изменения амплитуды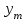 и фазы
и фазы 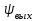 зависит как от свойств самого звена, так и от угловой частоты
зависит как от свойств самого звена, так и от угловой частоты 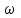 входного воздействия.
входного воздействия.
Отношение выходной величины звена (системы) к входной, выраженных в комплексной форме, называется комплексной частотной характеристикой (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ или АФХ).
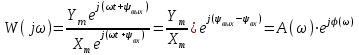
Рассмотрим линейную систему, находящуюся под влиянием задающего g(t) и возмущающегоf(t) воздействий (рис 6.1).

Рисунок 6.1 Структурная схема САР.
Передаточная функция регулятора:
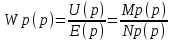
ПФ объекта по регулирующему воздействию:
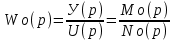
ПФ - ия объекта по возмущающему воздействию:
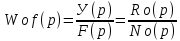
Операторное уравнение динамики объекта:
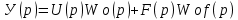 (1)
(1)С учетом 1 структурная схема (рисунок 6.1) может быть представлена в виде (рис. 6.2).
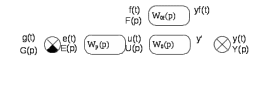
Рисунок 6.2 Упрощённая структурная схема
Если разорвать главную обратную связь и положить F(р)=0, то получим ПФ разомкнутой системы по задающему воздействию:
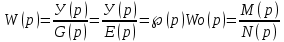
При этом структурная схема ( рис 6.2) упрощается (рис 6.3).
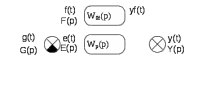
Рисунок 6.3 Структурная схема САР
Если разорвать главную обратную связь, то при
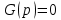 , получим ПФ разомкнутой системы по возмущающему воздействию:
, получим ПФ разомкнутой системы по возмущающему воздействию: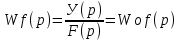
Рассмотрим теперь замкнутую систему (рисунок 6.3).
Передаточная функция замкнутой системы по задающему воздействию(при F(p)=0):
Ф(p)
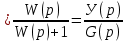
Учитывая, что
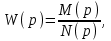
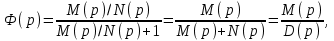
где N(p)- характеристический полином разомкнутой системы;
D(p)- характеристический полином замкнутой системы.
Рассмотрим возможные ПФ замкнутой системы. На основе схемы (рис. 6.3) составим сигнальный граф, где отобразим параметры системы
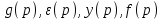 .
.
Рисунок 6.4 Сигнальный граф САР
При
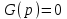
, получим ПФ- замкнутой системы по возмущающему воздействию:
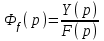 .
.По формуле Мэзона имеем:
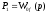 ;
;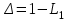 ;
; 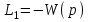 ;
;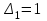 .
.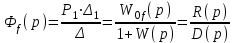 .
.По полученным ПФ можно записать операторное уравнение относительно регулируемой величины:
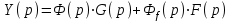 .
.Если в качестве выходной величины рассматривать сигнал ошибки
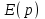 , а в качестве входной - сигнал задающего воздействия
, а в качестве входной - сигнал задающего воздействия 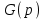 получим передаточную функцию замкнутой системы по ошибке от задающего воздействия.
получим передаточную функцию замкнутой системы по ошибке от задающего воздействия.Из рисунка 6.4 следует:
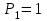 ;
; 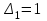 ;
; 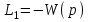
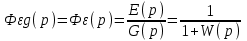 .
.Найдем связь между
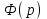 и
и 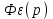 :
: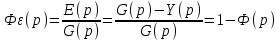 .
.Учитывая, что возмущение также влияет на отклонение регулируемой величины, а, следовательно, и на сигнал ошибки, то определим ПФ замкнутой системы по ошибке от возмущающего воздействия:
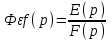 .
.Из рисунка 6.4:
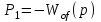 ;
; 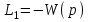 ;
; 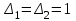
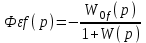 .
.Таким образом, результирующая ошибка системы имеет две составляющие:
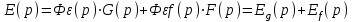 .
.§7 Временные характеристики линейных звеньев
В реальных условиях входные сигналы имеют произвольный характер. Для исследования динамических свойств звеньев (систем) следует выбирать такие типовые сигналы, которые по возможности наиболее близко отражали бы наиболее существенные особенности реальных сигналов. Кроме того, для сравнения отдельных элементов и систем между собой их также следует подвергать однотипным воздействиям. К числу наиболее часто применяемых типовых сигналов относятся:
- единичная ступенчатая функция 1(t);
- единичная импульсная функция
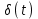 ;
;- гармоническая функция
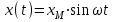 .
.Временной характеристикой звена (системы) по какому-либо внешнему воздействию называют закон изменения выходной величины звена при изменении внешнего воздействия по определенному закону и при условии, что до приложения внешнего воздействия звено находилось в покое (нулевые начальные условия).
1. Реакцию звена на воздействия в виде единичной ступенчатой функции
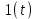 при нулевых начальных условиях называют переходной функцией
при нулевых начальных условиях называют переходной функцией 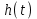 (рис. 7.1).
(рис. 7.1).Графическое изображение переходной функции называют переходной характеристикой.
















t
h(t)
1
0
t
x

Рисунок 7.1 Переходные характеристики линейных систем
Единичная ступенчатая функция определяется следующими условиями:
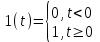 .
.Согласно определению ПФ изображение выходного сигнала:
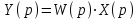 .
.Учитывая, что
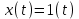
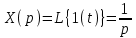 ,
,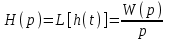 ,
,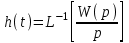 .
.2. Реакция звена на воздействие в виде единичной импульсной функции
 при нулевых начальных условиях называется весовой или импульсной переходной функцией
при нулевых начальных условиях называется весовой или импульсной переходной функцией 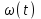 (рис 7.2).
(рис 7.2).Графическое изображение функции
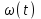 называется импульсной переходной характеристикой.
называется импульсной переходной характеристикой.










0
t
ω(t)
-δ(t)
t
x(t)
Рисунок 7.2 Импульсная переходная характеристика
Единичная импульсная функция или дельта-функция
 представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 7.2а).
представляет собой импульс бесконечно большой амплитуды и бесконечно малой длительности (рис. 7.2а).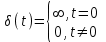 ;
;Математически дельта - функцию можно представить как производную от единичной ступенчатой функции:
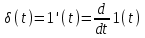 ,
,отсюда следует
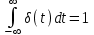
Учитывая, что входной сигнал
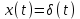 или
или 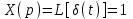 ,
,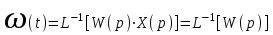
Переходная
 и импульсная
и импульсная 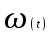 связаны соотношением:
связаны соотношением: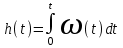 или
или 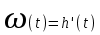
Обе временные характеристики
 и
и 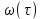 являются динамическими характеристиками и также полностью описывают свойства звена как ДУ и ПФ.
являются динамическими характеристиками и также полностью описывают свойства звена как ДУ и ПФ.
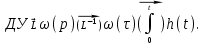
§8 Частотные характеристики линейных систем
При подаче на вход линейного звена гармонического воздействия
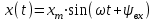 на выходе этого звена в установившемся режиме также будет получена гармоническая функция
на выходе этого звена в установившемся режиме также будет получена гармоническая функция 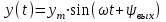 той же частоты
той же частоты 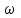 , но отличающаяся от входной по амплитуде и по фазе (рис. 8.1)
, но отличающаяся от входной по амплитуде и по фазе (рис. 8.1)
Рисунок 8.1 Гармонические сигналы
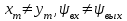
Изменения амплитуды
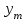 и фазы
и фазы 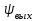 зависит как от свойств самого звена, так и от угловой частоты
зависит как от свойств самого звена, так и от угловой частоты 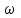 входного воздействия.
входного воздействия.Отношение выходной величины звена (системы) к входной, выраженных в комплексной форме, называется комплексной частотной характеристикой (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ или АФХ).