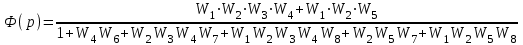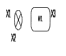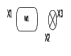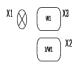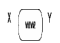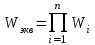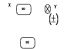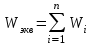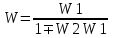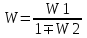ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 159
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(4)
передаточная функция звена по возмущающему воздействию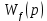
, при X(p)=0:
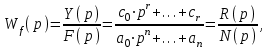(5)
из уравнений (4) и (5) следует, что
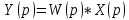
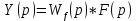(6)
Многочлен N(p),фигурирующий в знаменателе передаточных функций звена, называют характеристическим полином этого звена, а уравнение
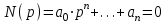
называется характеристическим уравнением звена. Оно представляет собой алгебраическое уравнение n-й степени и имеет n корней, среди которых могут быть как вещественные, так и комплексно-сопряженные.
Корни характеристического полинома называют полюсами передаточной функции, корни многочлена стоящего в числителе передаточной функции – нулями этой передаточной функции
Если известны передаточные функции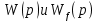
для звена на рисунке 1, то изображение выходной величины, согласно принципу суперпозиции:
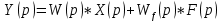
или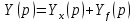
(7)
Соотношение (7) удобно представить в виде структурной схемы звена (рисунок 2).
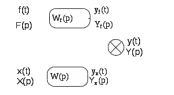
Рисунок 2 Структурная схема звена
ПРИМЕР 1: Дифференциальное уравнение звена имеет вид:
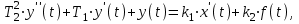(8)
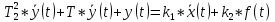Найти передаточные функции звена. Получить структурную схему.
РЕШЕНИЕ: По дифференциальному уравнению (8) составим операторное уравнение, используя преобразование по Лапласу и его свойства.
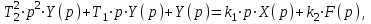
Полагая F(p)=0, найдем передаточную функцию звена по полезному сигналу.
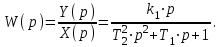
Полагая X(p)=0, найдем передаточную функцию звена по возмущающему воздействию:
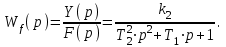
Структурная схема звена представлена на рисунке 2.
ПРИМЕР 2. Структурная схема звена имеет вид (рисунок. 2). Передаточные функции определяются по выражениям:
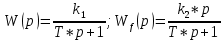
Найти дифференциальное уравнение звена.
РЕШЕНИЕ:
Операторное уравнение звена:
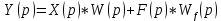
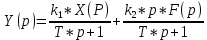
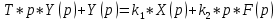
Применяя обратное преобразование Лапласа и его свойства, получим дифференциальное уравнение:
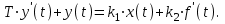
§ 4. Алгебра передаточных функций (ПФ). Основные соединения линейных звеньев.
Правила, позволяющие определить ПФ системы в целом по ПФ отдельных элементов, составляют алгебру ПФ.
Существуют три типа основных соединений звеньев: последовательное, параллельное и встречно-параллельное (обратное).
Последовательным, называют такое соединение двух или нескольких звеньев, при котором выходная величина предыдущего звена является входной величиной для последующего (рис 4.1)
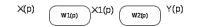
Рисунок 1 Последовательное соединение двух звеньев
По рисунку 4.1 получим операторные уравнения выходных сигналов элементов соединения (уравнения связи):
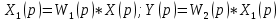
Исключая из уравнений промежуточную переменную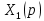
получим:
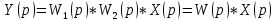
Откуда ПФ соединения:
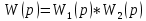
ОПРЕДЕЛЕНИЕ: ПФ последовательного соединения элементов равна произведению передаточных функций отдельных звеньев.
,
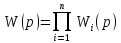где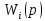
ПФ i-го звена,n- количество звеньев.
Параллельным называют такое соединение двух или нескольких звеньев, при котором входная величина у всех звеньев одна и та же, а выходные величины их суммируются (рис 4.2)
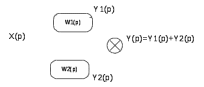
Рисунок 4.2 Параллельное соединение
Найдем операторные уравнения для выходных сигналов элементов соединения:
(
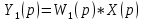
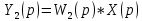
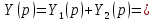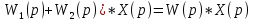
Следовательно
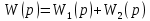
В общем случае при параллельном соединении n элементов:
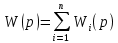
ПФ параллельного соединения равна сумме передаточных функций отдельных звеньев.
Обратным соединением двух звеньев или соединением с обратной связью (ОС) называют соединение, при котором выходная величина одного звена подается обратно на его вход через другое звено (рис 4.3).
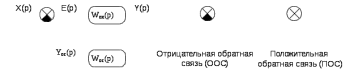
Рисунок 4.3 Соединение с обратной связью
Звено с ПФ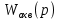
, стоящие в прямой цепи, называется звеном, охватываемым ОС.
Звено с ПФ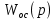
, стоящее в цепи обратной связи называют звеном обратной связи.
«+»
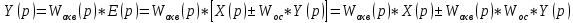
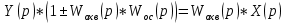
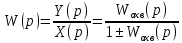
Для ООС
«-» для ПОС.
Важным частным случаем является единичная ООС когда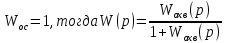
.
§5. Алгебра ПФ . Многоконтурная линейная одномерная САУ
Сложные системы содержат в своей структуре все типы соединений, рассмотренные выше. Если в САУ имеется более 1-го обратного соединения, то она является многоконтурной. Сложность получения ПФ таких систем определяется наличием перекрестных связей, элементов (сумматоров, звеньев, узлов).
Если известна структурная схема системы, то можно, пользуясь аппаратом структурных
преобразований (табл. 2), найти ПФ замкнутой САУ.
Правила переноса точки разветвления (узла).
Если узел переносится против направления прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями всех обойдённых звеньев.
Если узел переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с обратными передаточными функциями всех обойдённых звеньев.
Правила переноса сумматора.
Если сумматор переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включать элементы с передаточными функциями всех обойдённых при переносе звеньев.
Если сумматор переносится против прохождения сигнала, то в переносимую ветвь нужно включать элементы с обратными передаточными функциями всех обойдённых звеньев.
Приведённые правила отражены в таблице 2.
Для систем со сложными взаимосвязями параметров состояния метод структурных преобразований может оказаться трудоемким. Метод сигнальных графов, разработанный Мэзоном, позволяет избежать операций по упрощению структурных схем и воспользоваться формулой расчета передаточной функции.
Сигнальный граф-это диаграмма, состоящая из точек (узлов), соединенных направленными ветвями, и являющаяся графическим представлением дифференциальных уравнений или ПФ, описывающих работу системы.
Узлы графа – точки, соответствующие параметрам состояния процессов в системе (сигналам).
Ветвь – линия, соединяющая два узла.Каждая ветвь Wi характеризуется передаточной функцией.
Путь – ветвь иди последовательность ветвей, связывающих два узла графа.
Контур обратной связи – замкнутый путь, состоящий из ряда ветвей, возвращающихся в исходный узел.
В общем случае ПФ - ия W м/б неизвестной или переменной Хi и Хj задается формулой Мэйзона
Wij=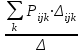
,
где Рijk – передаточная функция к – го пути от хi к xj .Определяется последовательным перемножением ПФ всех ветвей данного пути.
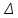
- определитель графа;
ijк – адьюнкт к – го пути.
Определитель определяется по следующему правилу:
∆ = 1- (сумма передач всех контуров)+ (сумма передач всех контуров, не касающихся друг друга, перемноженных попарно) – (сумма перемноженных передач из трёх не касающихся друг друга контуров) + ….
Два контура не касаются друг друга, если они не имеют ни одной общей вершины.
Адьюнкт к-го пути определяется по правилу:
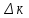=1-(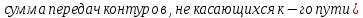
Пример. Для рассмотренных типовых соединений линейных звеньев сигнальные графы имеют вид (рис 5.1 а, б, в, г.).
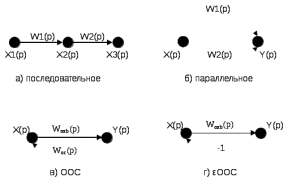
Рисунок 5.1 Сигнальные графы для типовых соединений звеньев
Пример. Структурная схема системы имеет вид (рисунок 5.2). Найдем ПФ, пользуясь методом сигнальных графов.
Рисунок 5.2 Пример многоконтурной САУ
Рисунок 5.3 Сигнальный граф многоконтурной САУ
На рисунке 5.3 изобразим сигнальный граф системы (рисунок 5.2). Имеется 2 пути от точки входа Х(р) к точке выхода У(р):
P1=W1W2W3W4 ; P2=W1W2W5 .
На приведённой схеме пять контуров:
L1=-W4W6 ; L2=-W2W3W4W7; L3=-W1W2W3W4W8; L4=-W2W5W7; L5=-W1W2W5W8 .
Так как все контура касаются как первого так и второго пути, то адьюнкты данных путей равны ∆1=∆2=1.
Так как в приведённой схеме отсутствуют контура не касающиеся друг друга, то формула Мэзона для данного примера примет вид:
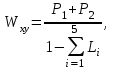
Окончательно, передаточная функция замкнутой системы:
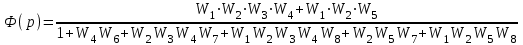
передаточная функция звена по возмущающему воздействию
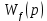, при X(p)=0: 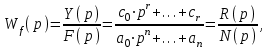(5) из уравнений (4) и (5) следует, что
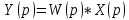
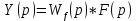(6)Многочлен N(p),фигурирующий в знаменателе передаточных функций звена, называют характеристическим полином этого звена, а уравнение
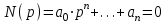
называется характеристическим уравнением звена. Оно представляет собой алгебраическое уравнение n-й степени и имеет n корней, среди которых могут быть как вещественные, так и комплексно-сопряженные.
Корни характеристического полинома называют полюсами передаточной функции, корни многочлена стоящего в числителе передаточной функции – нулями этой передаточной функции
Если известны передаточные функции
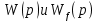для звена на рисунке 1, то изображение выходной величины, согласно принципу суперпозиции: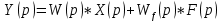 или
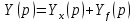(7)Соотношение (7) удобно представить в виде структурной схемы звена (рисунок 2).
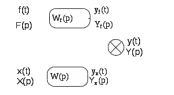
Рисунок 2 Структурная схема звена
ПРИМЕР 1: Дифференциальное уравнение звена имеет вид:
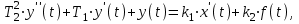(8)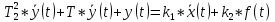 Найти передаточные функции звена. Получить структурную схему.РЕШЕНИЕ: По дифференциальному уравнению (8) составим операторное уравнение, используя преобразование по Лапласу и его свойства.
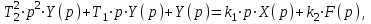
Полагая F(p)=0, найдем передаточную функцию звена по полезному сигналу.
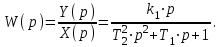
Полагая X(p)=0, найдем передаточную функцию звена по возмущающему воздействию:
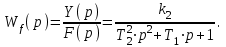
Структурная схема звена представлена на рисунке 2.
ПРИМЕР 2. Структурная схема звена имеет вид (рисунок. 2). Передаточные функции определяются по выражениям:
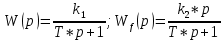
Найти дифференциальное уравнение звена.
РЕШЕНИЕ:
Операторное уравнение звена:
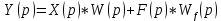
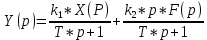
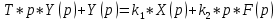
Применяя обратное преобразование Лапласа и его свойства, получим дифференциальное уравнение:
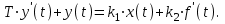
§ 4. Алгебра передаточных функций (ПФ). Основные соединения линейных звеньев.
Правила, позволяющие определить ПФ системы в целом по ПФ отдельных элементов, составляют алгебру ПФ.
Существуют три типа основных соединений звеньев: последовательное, параллельное и встречно-параллельное (обратное).
Последовательным, называют такое соединение двух или нескольких звеньев, при котором выходная величина предыдущего звена является входной величиной для последующего (рис 4.1)
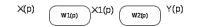
Рисунок 1 Последовательное соединение двух звеньев
По рисунку 4.1 получим операторные уравнения выходных сигналов элементов соединения (уравнения связи):
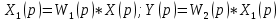
Исключая из уравнений промежуточную переменную
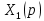получим: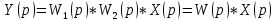 Откуда ПФ соединения:
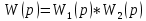
ОПРЕДЕЛЕНИЕ: ПФ последовательного соединения элементов равна произведению передаточных функций отдельных звеньев.
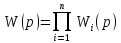,где
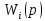ПФ i-го звена,n- количество звеньев.Параллельным называют такое соединение двух или нескольких звеньев, при котором входная величина у всех звеньев одна и та же, а выходные величины их суммируются (рис 4.2)
Рисунок 4.2 Параллельное соединение
Найдем операторные уравнения для выходных сигналов элементов соединения:
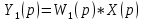
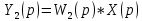
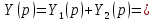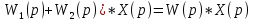
( Следовательно
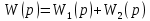
В общем случае при параллельном соединении n элементов:
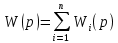
ПФ параллельного соединения равна сумме передаточных функций отдельных звеньев.
Обратным соединением двух звеньев или соединением с обратной связью (ОС) называют соединение, при котором выходная величина одного звена подается обратно на его вход через другое звено (рис 4.3).
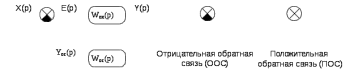
Рисунок 4.3 Соединение с обратной связью
Звено с ПФ
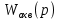, стоящие в прямой цепи, называется звеном, охватываемым ОС.Звено с ПФ
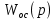, стоящее в цепи обратной связи называют звеном обратной связи. «+»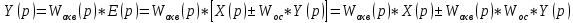
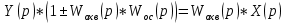
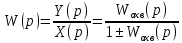
Для ООС
«-» для ПОС.
Важным частным случаем является единичная ООС когда
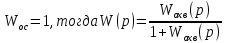.§5. Алгебра ПФ . Многоконтурная линейная одномерная САУ
Сложные системы содержат в своей структуре все типы соединений, рассмотренные выше. Если в САУ имеется более 1-го обратного соединения, то она является многоконтурной. Сложность получения ПФ таких систем определяется наличием перекрестных связей, элементов (сумматоров, звеньев, узлов).
-
Метод структурных преобразований.
Если известна структурная схема системы, то можно, пользуясь аппаратом структурных
|
преобразований (табл. 2), найти ПФ замкнутой САУ.
Правила переноса точки разветвления (узла).
Если узел переносится против направления прохождения сигнала, то в переносимую ветвь нужно включить элементы с передаточными функциями всех обойдённых звеньев.
Если узел переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включить элементы с обратными передаточными функциями всех обойдённых звеньев.
Правила переноса сумматора.
Если сумматор переносится по направлению прохождения сигнала, то в переносимую ветвь нужно включать элементы с передаточными функциями всех обойдённых при переносе звеньев.
Если сумматор переносится против прохождения сигнала, то в переносимую ветвь нужно включать элементы с обратными передаточными функциями всех обойдённых звеньев.
Приведённые правила отражены в таблице 2.
-
Метод сигнальных графов.
Для систем со сложными взаимосвязями параметров состояния метод структурных преобразований может оказаться трудоемким. Метод сигнальных графов, разработанный Мэзоном, позволяет избежать операций по упрощению структурных схем и воспользоваться формулой расчета передаточной функции.
Сигнальный граф-это диаграмма, состоящая из точек (узлов), соединенных направленными ветвями, и являющаяся графическим представлением дифференциальных уравнений или ПФ, описывающих работу системы.
Узлы графа – точки, соответствующие параметрам состояния процессов в системе (сигналам).
Ветвь – линия, соединяющая два узла.Каждая ветвь Wi характеризуется передаточной функцией.
Путь – ветвь иди последовательность ветвей, связывающих два узла графа.
Контур обратной связи – замкнутый путь, состоящий из ряда ветвей, возвращающихся в исходный узел.
В общем случае ПФ - ия W м/б неизвестной или переменной Хi и Хj задается формулой Мэйзона
Wij=
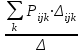,где Рijk – передаточная функция к – го пути от хi к xj .Определяется последовательным перемножением ПФ всех ветвей данного пути.
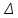
- определитель графа;
ijк – адьюнкт к – го пути.Определитель
определяется по следующему правилу:∆ = 1- (сумма передач всех контуров)+ (сумма передач всех контуров, не касающихся друг друга, перемноженных попарно) – (сумма перемноженных передач из трёх не касающихся друг друга контуров) + ….
Два контура не касаются друг друга, если они не имеют ни одной общей вершины.
Адьюнкт к-го пути определяется по правилу:
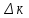=1-(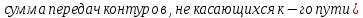 Пример. Для рассмотренных типовых соединений линейных звеньев сигнальные графы имеют вид (рис 5.1 а, б, в, г.).
Рисунок 5.1 Сигнальные графы для типовых соединений звеньев
Пример. Структурная схема системы имеет вид (рисунок 5.2). Найдем ПФ, пользуясь методом сигнальных графов.
Рисунок 5.2 Пример многоконтурной САУ
Рисунок 5.3 Сигнальный граф многоконтурной САУ
На рисунке 5.3 изобразим сигнальный граф системы (рисунок 5.2). Имеется 2 пути от точки входа Х(р) к точке выхода У(р):
P1=W1W2W3W4 ; P2=W1W2W5 .
На приведённой схеме пять контуров:
L1=-W4W6 ; L2=-W2W3W4W7; L3=-W1W2W3W4W8; L4=-W2W5W7; L5=-W1W2W5W8 .
Так как все контура касаются как первого так и второго пути, то адьюнкты данных путей равны ∆1=∆2=1.
Так как в приведённой схеме отсутствуют контура не касающиеся друг друга, то формула Мэзона для данного примера примет вид:
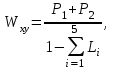
Окончательно, передаточная функция замкнутой системы: