Файл: Задача эц расчет трехфазной цепи 15 Задача мц расчет характеристик силовых трансформаторов 22.doc
Добавлен: 06.11.2023
Просмотров: 64
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки И ВЫСШЕГО образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Уфимский государственный нефтяной технический университет»
Институт нефтепереработки и нефтехимии ФГБОУ ВО УГНТУ в г. Салавате
Кафедра «Электрооборудование и автоматика промышленных предприятий»
Электротехника и электроника
Расчет параметров электрической цепи
ЭАПП-15.03.04-01.02.02 Р
| Исполнитель: студент гр. БАТсз-22-21 | В.Д. Якушев |
| Преподаватель: ассистент | К.В. Чернов |
Салават
2023
Оглавление
Задача ЭЦ-1. Расчет линейной электрической цепи постоянного тока 3
Задача ЭЦ-2. Расчет электрической цепи однофазного переменного тока 10
Задача ЭЦ-3. Расчет трехфазной цепи 15
Задача МЦ-1. Расчет характеристик силовых трансформаторов 22
Задача ЭМ-1. Расчет характеристик асинхронных двигателей 29
Список используемой литературы 32
Задача ЭЦ-1. Расчет линейной электрической цепи постоянного тока
Задание:
1. Определить токи в ветвях с помощью уравнений, составленных по законам Кирхгофа.
2. Составить уравнение баланса мощностей.
3. Определить показания вольтметра.
4. Определить ток Ι1 в ветви c сопротивлением R1 по методу эквивалентного генератора и построить график зависимости
Схема цепи представлена на рисунке 1. Значения параметров цепи указаны в таблице 1.
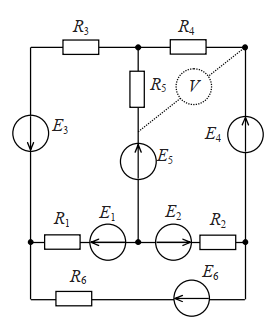
Рисунок 1 – Схема электрической цепи
Таблица 1 – Исходные данные
| E3, В | E4, В | E5, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом |
| 54 | 10 | 19 | 39 | 43 | 34 | 91 | 26 | 79 |
Решение:
1. Определим токи в ветвях с помощью уравнений, составленных по законам Кирхгофа.
Для определения токов в ветвях цепи по законам Кирхгофа необходимо составить
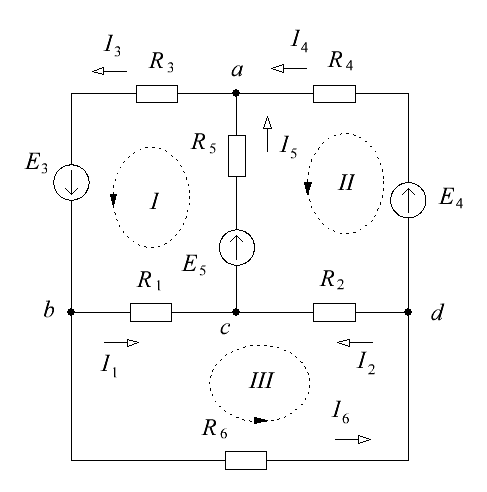
Рисунок 2 – Расчетная схема электрической цепи
Уравнение по первому закону Кирхгофа составляем для узлов a, bиc. Обход контуров производим в направлении, показанном на рисунке 2.
 ,
,Подставляем числовые значения сопротивлений и ЭДС. В результате получим систему уравнений:
 ,
,,
В результате решения данной системы уравнений, получим следующие значения токов в ветвях:
2. Составим баланс мощностей в расчетной схеме.
Согласно закону сохранения энергии мощность, вырабатываемая источниками энергии, равна суммарной мощности приемников электрической энергии. Уравнение баланса мощностей имеет вид:
Мощность источников ЭДС:
Суммарная мощность приемников:
Баланс мощностей выполняется:
3. Определим показание вольтметра из уравнения, составленного по второму закону Кирхгофа:
4. Определим ток Ι1 в ветви c сопротивлением R1 по методу эквивалентного генератора.
Ток Ι1 по методу эквивалентного генератора может быть выражен следующим образом:
Определим напряжение холостого хода и входное сопротивление.
Изобразим схему электрической цепи без первой ветви и обозначим на ней токи в ветвях (см. рис. 3).
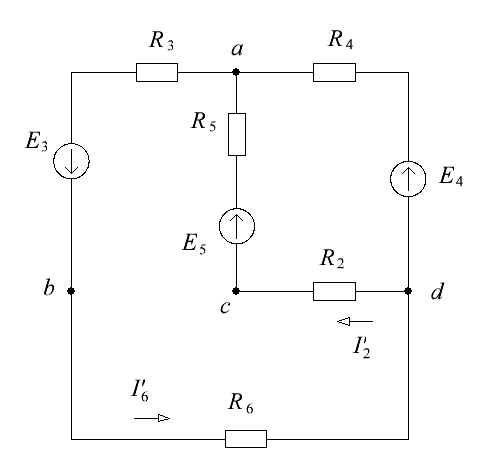
Рисунок 3 – Схема эквивалентного генератора
Определим токи в ветвях, применив метод двух узлов:
где проводимости ветвей:
Определим токи в ветвях:
Напряжение холостого хода определяем из уравнения, составленного по второму закону Кирхгофа для второго контура:
Определим входное сопротивление генератора. Исключим из цепи все источники ЭДС и определим сопротивление относительно узлов с и b. Заменим треугольник сопротивлений
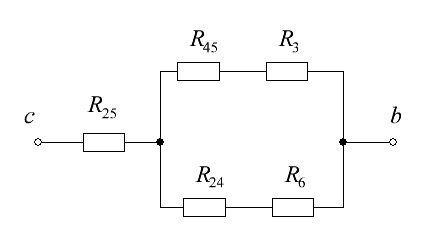
Рисунок 4 – Схема для определения входного сопротивления
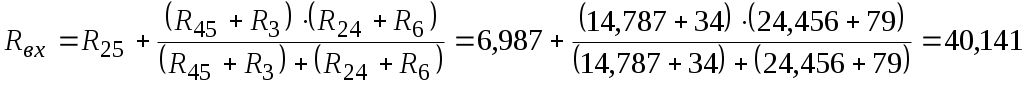 Ом.
Ом.Ток
5. Построим график зависимости
В п. 4 была получена зависимость
.
Задаваясь значениями сопротивления
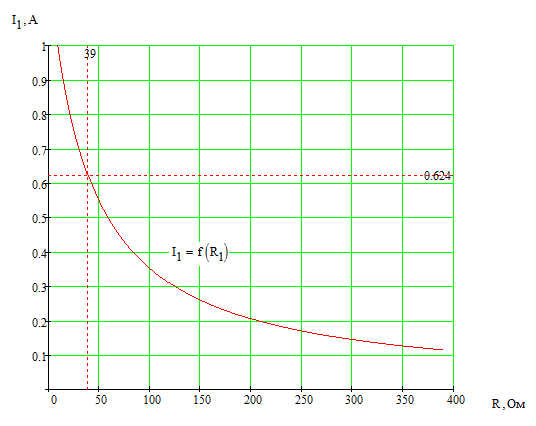
Рисунок 5 – График зависимости