Файл: Лабораторная работа для ипз. Проект. 1 Общие положения и задание 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вывод: На основе графика можно выдвинуть гипотезу, что зависимость есть, обратная.
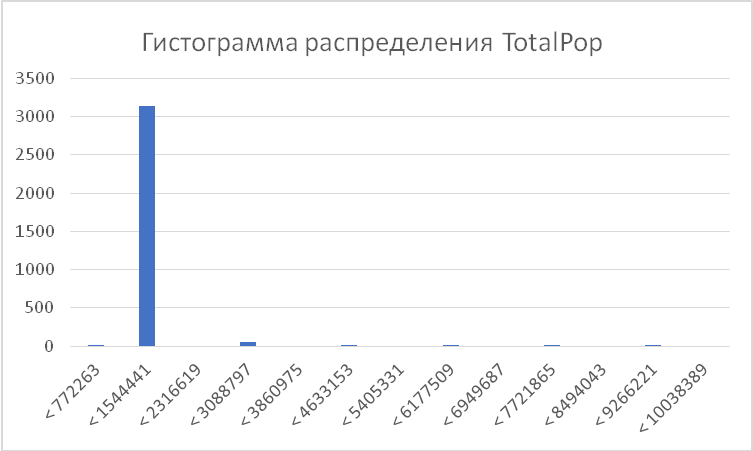
3.1.2 Гистограмма распределения
Задача 2. Какие значения численности населения распределены по интервалам с шагом?
Нужно построить гистограмму распределения значений признака численность населения.
Гистограмма распределения отражает частоты попадания значений количественного признака в интервалы. Это НЕ диаграмма Гистограмма.
Построить можно, воспользовавшись надстройкой Пакет анализа.
Но в данной работе сделаем вручную.
Последовательность действий:
-
определить количество интервалов у гистограммы; используем формулу Стёрджеса N=1+log2(n)=1+log2(3221)=13. Здесь n -объём выборки. -
определить ширину интервала (с учетом округления); Найдем минимальное и максимальное значения, их разность разделим на N -
определить границу первого интервала; -
сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту); Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() -
построить гистограмму. Диаграмма Гистограмма с группировкой
| Числовые харак-ки TotalPop | |
| Объём выборки, n | 3221 |
| Число интервалов, N | 13 |
| Минимальное значение | 85 |
| Максимальное значение | 10038388 |
| Ширина интервала | 772178 |
| Интервалы | Обозначение интервала | Нижняя граница | Верхняя граница | Частота |
| 1 | < 772263 | 85 | 772263 | 1 |
| 2 | < 1544441 | 772263 | 1544441 | 3144 |
| 3 | < 2316619 | 1544441 | 2316619 | 0 |
| 4 | < 3088797 | 2316619 | 3088797 | 52 |
| 5 | < 3860975 | 3088797 | 3860975 | 0 |
| 6 | < 4633153 | 3860975 | 4633153 | 14 |
| 7 | < 5405331 | 4633153 | 5405331 | 0 |
| 8 | < 6177509 | 5405331 | 6177509 | 3 |
| 9 | < 6949687 | 6177509 | 6949687 | 0 |
| 10 | < 7721865 | 6949687 | 7721865 | 2 |
| 11 | < 8494043 | 7721865 | 8494043 | 0 |
| 12 | < 9266221 | 8494043 | 9266221 | 2 |
| 13 | < 10038389 | 9266221 | 10038389 | 0 |
3.2. Визуализация: качественные признаки.
3.2.1 Частотная таблица
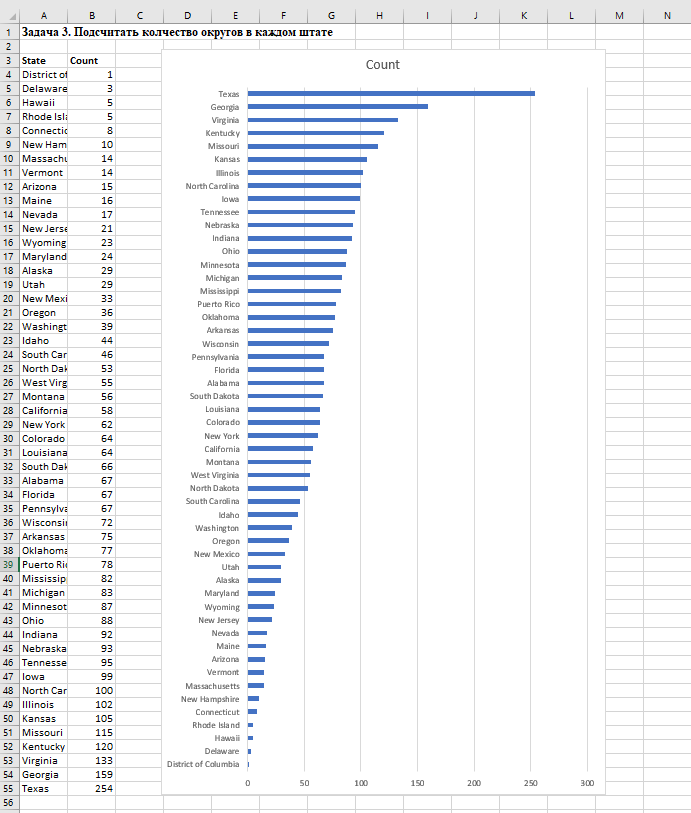
Задача 3. Подсчитать колчество округов в каждом штате
Это и будет частотная таблица
Для этого подсчитаем, сколько раз название каждого штата встретилось (частоту появления признака Штат)
Сделать можно с помощью расширенного фильтра
(Данные – блок Сортировка и Фильтр – Дополнительно (Расширенный фильтр)
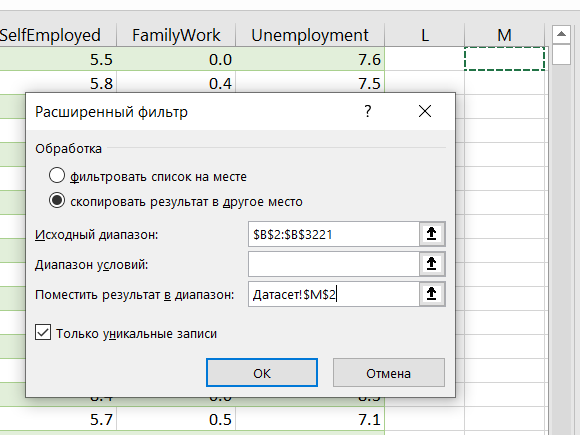
Замечание. Список уникальных значений можно разместить только на тот же лист.
Затем подсчитаем количество вхождений каждого названия штата в столбик State с помощью функции =СЧЁТЕСЛИ($B$2:$B$3221;M3) – аргументы приведены для примера
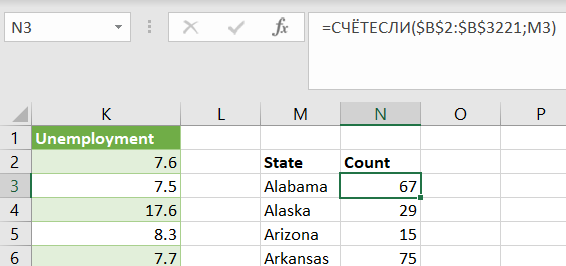
Перенесем полученные данные на лист Качественные прзнаки, отсортируем и построим диаграмму
3.2.2 Таблица сопряженности
Задача 4.
В данном датасете мало качественных признаков, поэтому пришлось изобрести свои.
Для второй задачи введем два бинарных признака ( да – нет):
PublicWork _bin – уровень занятых в государственном секторе выше, чем медианное значение по стране
Unemployment l_bin - уровень безработицы выше, чем медианное значение по стране
Выяснить, как распределены округа по этим двум признакам. Составть таблицу сопряженности для этих двух признаков.
Решение.
Для заполнения значений обоих признаков используем функциию =ЕСЛИ(...)
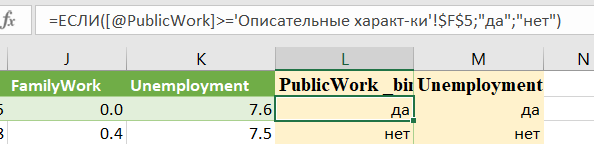
Составим таблицу сопряженности для этих двух бинарных признаков. Для этого сформруем сводную таблицу (Вставить – Сводная таблица)
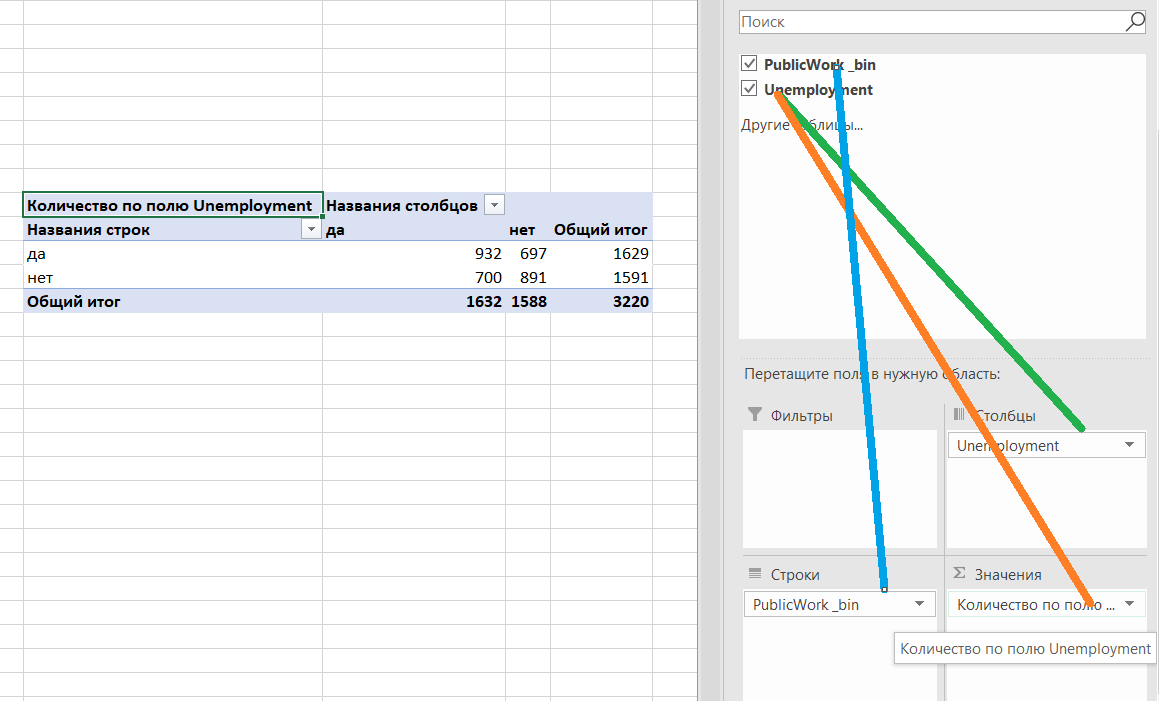
В итоге получаем следующую таблицу сопряженности.
| | Unemployment_bin % | ||
| PublicWork _bin | да | нет | n |
| да | 57.2 | 42.8 | 1629 |
| нет | 44 | 56 | 1591 |
| Общий итог | 1632 | 1588 | 3220 |
Вывод. Округа с различающимся уровнем присутствия гос. сектора сильно различаются по уровню безработицы (гипотеза).
Методики анализа и проверки гипотез таких таблиц широко применяются гуманитариями, но их рассмотрение выходит за рамки данного курса.
3.3. Визуализация: Количественный и качественный признаки.
При таком сочетании, как правило, интересуются распределенем количественного признака при разных значениях качественного.
3.3.1 Распределение количественного признака для разных значений (категорий) качественного
Задача 5. Построим распределене доходов в завсимости от признака Unemployment_bin: превышает в округе уровень безработицы медианный уровень.
Используем статистические диаграммы – ящик с усами.
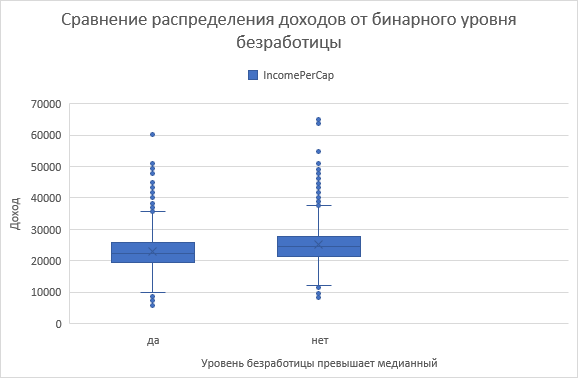
Вывод. Распределение подущевого дохода зависит от уровня безработицы (гипотеза)
Проверка гипотезы – за рамками курса.
3.3.2 Линейчатая диаграмма с категориями
Задача 6. Визуализировать, как распределены доли рабочих мест по разным видам собственности в округе с минимальным уровнем безработицы в сравнении с округом с максимальным уровнем безработицы.
Имеем пять количественных признаков– уровень безработицы и дол занятых в разных видах собственности. Извлечем из данных нужную информацию и построим диаграмму.
Найдем округ с максимальным уровнем безработицы и с минимальным, скопируем соответствующие строки, построим линейчатую диаграмму
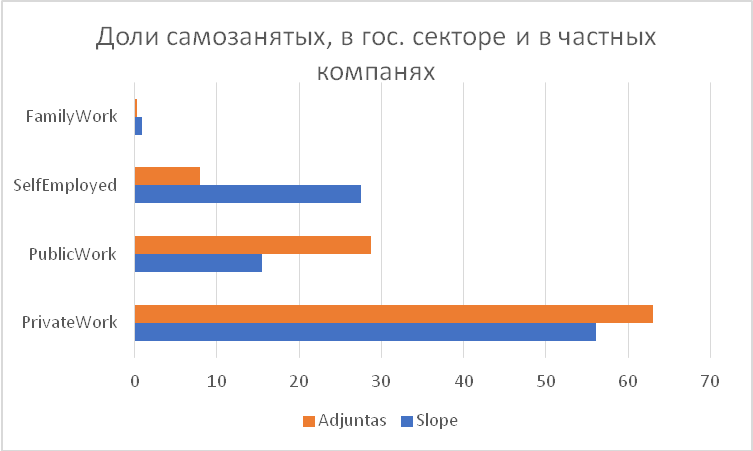
Вывод: В округе с минимальной безработицей доля самозанятых превосходит долю занятых в госуд. секторе. В округе с максимальной безработицей - наоборот.
Можно выдвинуть гипотезы, что уровень безработицы связан с долей самозанятых и долей рабочих мест, принадлежащих госуд. структурам.
Но проверять их нужно на всех выборках с помощью соответствующих методов проверки гипотез, а не по одной паре случаев.