Файл: Контрольная работа по дисциплине "Гидравлика" Вариант 15 Татков Н. С. Группа пгскдз21 Иваново 2022 Вопрос 8.doc

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

“Ивановский Государственный политехнический университет”
Кафедра гидравлики, теплотехники и инженерных сетей

Контрольная работа

по дисциплине “Гидравлика”

Вариант 15


Выполнил:

Татков Н.С.

Группа:

ПГСКДЗ-21
Иваново 2022

Вопрос 8

Что такое «идеальная жидкость»? В чем основные отличия реальной жидкости от идеальной?

Идеальная жидкость – модель природной жидкости, характеризующаяся изотропно­стью всех физических свойств и, кроме того, характеризуется абсолютной несжимаемо­стью, абсолютной текучестью (отсутствие сил внутреннего трения), отсутствием процес­сов теплопроводности и теплопереноса.

Реальная жидкость – модель природной жидкости, характеризующаяся изотропно­стью всех физических свойств, но в отличие от идеальной модели, обладает внутренним трением при движении.

Вопрос 29

Запишите уравнение неразрывности движущейся жидкости в случае установившегося движения.

Уравнение неразрывности для потока жидкости

ρ₁V₁ω₁ = ρ₂V₂ω₂,

а при движении несжимаемой жидкости (ρ = const)

V₁ω₁ = V₂ω_2.

Из этого следует, что при уменьшении площади живого сечения при движении несжимаемой жидкости средняя скорость увеличивается, а при увеличении площади – уменьшается.

Вопрос 44

Напишите основное уравнение установившегося равномерного движения и объясните входящие в это уравнение величины.

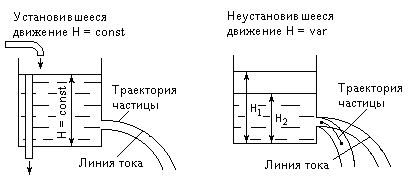
Рис. 44.1 Рис. 44.2

Понятие установившегося движения вводится только при исследовании движения жидкости в переменных Эйлера.

Установившимся называется движение жидкости, при котором все элементы, характеризующие движение, в любой точке пространства не меняются во времени (см. рис. 44.1). Например, для составляющих скорости будем иметь

---

;

;

.

Отсюда

; ; .

Тогда

;

;

,

где – проекции ускорения движущейся частицы на соответствующие координатные оси.

Частные производные

, ,

называются проекциями локального (местного) ускорения.

Суммы вида



называется проекциями конвективного ускорения.

Полные производные

, ,

называют еще субстанциональными или индивидуальными производными.

Так как величина и направление скорости движения в любой точке пространства при установившемся движении не меняются, то и линии тока не будут меняться во времени. Отсюда следует, что при установившемся движении траектории частиц и линии тока совпадают.

Движение, при котором все элементы, характеризующие движение жидкости, в любой точке пространства меняются во времени, называется неустановившимся ( , см. рис. 44.2).

Вопрос 56

Как рассчитать общую потерю давления на трение при последовательном соединении труб?

---

Когда нужно найти потерю энергии в трубопроводе, составленном из нескольких прямых последовательных участков и нескольких местных сопротивлений можно использовать следующую формулу

h = ∑h_тр + ∑h_м = ∑λ + ∑λ = λ = λ .

Приведенная длина трубопровода определяется по формуле

l_пр = l + l_экв,

где l – общая длина трубопровода;

l_экв – эквивалентная длина местного сопротивления, т.е. длина прямого участка трубы, потери на трение на которой равны потерям в данном местном сопротивлении, м;

l_экв = ;

Вопрос 67

Что называется малым отверстием в тонкой стенке? Объясните смысл коэффициентов сжатия, скорости и расхода.

Отверстие считается в тонкой стенке в случае, если толщина стенки не влияет на условия истечения. При этом вытекающая жидкость касается только кромки отверстия, что может быть обеспечено либо срезом кромок под острым углом, либо при толщине стенки δ ≤ 0,5d. Постоянство напора Н обеспечивается поступлением жидкости в резервуар с расходом q, равным расходу истечения Q.

Коэффициентом сжатия струи ε называется отношение площади поперечного сечения сжатой струи ω_сж к площади сечения отверстия ω:

ε = ω_сж/ω

Коэффициент расхода μ характеризует уменьшение расхода вязкой жидкости по сравнению с расходом невязкой жидкости вследствие возникающих потерь энергии и сжатия струи:

μ = φε.

Коэффициент скорости φ всегда меньше единицы и характеризует уменьшение скорости вязкой (реальной) жидкости по сравнению со скоростью невязкой жидкости за счет потерь энергии при протекании через отверстие.

---

Вопрос 80

Какие безразмерные комплексы является критериями динамического подобия? Назовите их.

Запишем уравнение движения в безразмерном виде, для чего разделим его почленно на /l₀:

– + =

= + + + . (1)

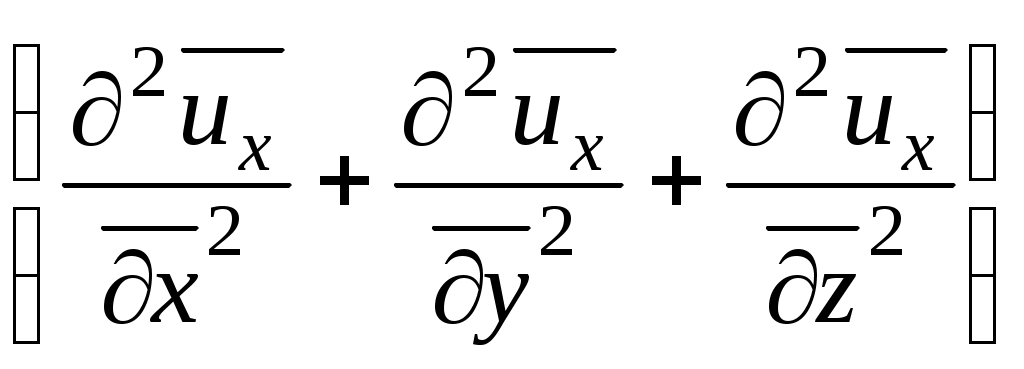В уравнении (1) все слагаемые безразмерны, безразмерны и комплексы, составленные их характеристик физических величин, эталонов.

Для подобных потоков безразмерные уравнения одинаковы, что возможно только тогда, когда соответственные коэффициенты, в нашем случае безразмерные комплексы, также одинаковы:

= idem; = idem; = idem; = idem.

Записанные безразмерные комплексы являются критериями динамического подобия

= Fr – критерий Фруда;

---

= Eu – критерий Эйлера;

= Re – критерий Рейнольдса;

= Ho = Sh – критерий гомохронности или критерий Струхаля.

Задача 8

В закрытом сосуде с водой давление на свободной поверхностиp₀ = 12 кПа (плотность воды ρ = 1000 кг/м³). Точка В заглублена под уровень на h = 0,5 м. Определить абсолютное давление p_аб, действующее на т. В.

Решение.

Абсолютное давление в любой точке покоящейся жидкости складывается из давления на свободной поверхности p₀ и давления, определяемого весом столба жидкости, ρgh

p_аб = p₀ + ρgh.

Тогда абсолютное давление, действующее на т. В в закрытом сосуде, равно

p_аб = p₀ + ρgh = 12000 + 1000 · 9,81 · 0,5 = 16905 Па.

Ответ:p_аб = 16905 Па.

Задача 29

Дюкер, выполненный из стальных труб диаметром d = 400 мм и весом G_тр = 990 Н, должен опускаться на дно реки без заполнения водой. Определить необходимый объем дополнительного бетонного груза V_б для обеспечения затопления трубопровода на 1 м его длины. Плотность бетона ρ_б = 2500 кг/м³, а плотность воды ρ_в = 999,73 кг/м³.

Решение.

Вес 1 м трубопровода с бетонным грузом определим по формуле

G = G_тр + G_б = G_тр + ρ_бgV_б.

Выталкивающая сила воды, приходящаяся на 1 м длины трубопровода, по закону Архимеда

P_выт = ρ_вg(V_тр + V_б) = ρ_вg(ωl + V_б).

где ω – площадь поперечного сечения трубопровода,

ω = = = 0,1256 м².

Таким образом

G_тр + ρ_бgV_б = ρ_вg(ωl + V_б).

Откуда объем дополнительного бетонного груза

V_б = = = 0,0164 м³.

Ответ: V_б = 0,0164 м³.

Задача 44

Определить минимальный расход воздуха, при котором в трубе диаметром d = 0,2 м сохраняется турбулентный режим. Плотность воздуха ρ = 1,2 кг/м³, коэффициент динамической вязкости μ = 18 · 10^-6 Па · с.

---