Файл: Информация и формы ее представления Информационные процессы и технологии.docx

Перспективы развития вычислительных средств

Появление новых поколений ЭВМ обусловлено расширением сферы их применения, требующей более производительной, дешевой и надежной вычислительной техники. В настоящее время стремление к реализации новых потребительских свойств ЭВМ стимулирует работы по созданию машин пятого и последующего поколений. Вычислительные средства пятого поколения, кроме более высокой производительности и надежности при более низкой стоимости, обеспечиваемых новейшими электронными технологиями, должны удовлетворять качественно новым функциональным требованиям:

• 
  работать с базами знаний в различных предметных областях и организовывать на их основе системы искусственного интеллекта;
  
• 
  обеспечивать простоту применения ЭВМ путем реализации эффективных систем ввода-вывода информации голосом, диалоговой обработки информации с использованием естественных языков, устройств распознавания речи и изображения;
  
• 
  упрощать процесс создания программных средств путем автоматизации синтеза программ.
  

В настоящее время ведутся интенсивные работы как по созданию ЭВМ пятого поколения традиционной (неймановской) архитектуры, так и по созданию и апробации перспективных архитектур и схемотехнических решений. На формальном и прикладном уровнях исследуются архитектуры на основе параллельных абстрактных вычислителей (матричные и клеточные процессоры, систолические структуры, однородные вычислительные структуры, нейронные сети и др.) Развитие вычислительной техники с высоким параллелизмом во многом определяется элементной базой, степенью развития параллельного программного обеспечения и методологией распараллеливания алгоритмов решаемых задач.

Проблема создания эффективных систем параллельного программирования, ориентированных на высокоуровневое распараллеливание алгоритмов вычислении и обработки данных, представляется достаточно сложной и предполагает дифференцированный подход с учетом сложности распараллеливания и необходимости синхронизации процессов во времени.

Наряду с развитием архитектурных и системотехнических решений ведутся работы по совершенствованию технологий производства интегральных схем

---

и по созданию принципиально новых элементных баз, основанных на оптоэлектронных и оптических принципах.

В плане создания принципиально новых архитектур вычислительных средств большое внимание уделяется проектам нейрокомпьютеров, базирующихся на понятии нейронной сети (структуры на формальных нейронах), моделирующей основные свойства реальных нейронов. В случае применения био- или оптоэлементов могут быть созданы соответственно биологические или оптические нейрокомпьютеры. Многие исследователи считают, что в следующем веке нейрокомпьютеры в значительной степени вытеснят современные ЭВМ, используемые для решения трудно формализуемых задач. Последние достижения в микроэлектронике и разработка элементной базы на основе биотехнологий дают возможность прогнозировать создание биокомпьютеров.

Важным направлением развития вычислительных средств пятого и последующих поколений является интеллектуализация ЭВМ, связанная с наделением ее элементами интеллекта, интеллектуализацией интерфейса с пользователем и др. Работа в данном направлении, затрагивая, в первую очередь, программное обеспечение, потребует и создания ЭВМ определенной архитектуры, используемых в системах управления базами знаний, — компьютеров баз знаний, а так же других подклассов ЭВМ. При этом ЭВМ должна обладать способностью к обучению, производить ассоциативную обработку информации и вести интеллектуальный диалог при решении конкретных задач.

В заключение отметим, что ряд названных вопросов реализован в перспективных ЭВМ пятого поколения либо находится в стадии технической проработки, другие — в стадии теоретических исследований и поисков.

1.4 Представление данных в памяти компьютера

Данные в компьютере представляют собой двоичный код. Поэтому возникает проблема представления произвольного набора данных в двоичном виде.

Представление целых беззнаковых чисел

Проще всего эта проблема решается для случая целых беззнаковых (то есть, все данные имеют только один знак, который поэтому можно опустить) чисел. Перевод такого числа из десятичной системы в двоичную можно осуществить с помощью целочисленного деления по следующему алгоритму:

---

1. 
   Если текущее число меньше 2, то записать его в младший разряд результата, выполнение прекратить. Иначе, разделить текущее число с остатком на 2.
   
2. 
   Остаток записать в младший разряд результата.
   
3. 
   Применить пункт 1 к частному.
   

Это можно наглядно продемонстрировать с помощью деления «уголком».



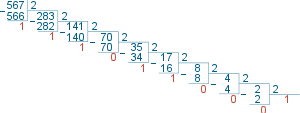
Деление «уголком»

Теперь достаточно записать справа налево выделенные цифры, и получится ответ: 10 00110111. Чтобы представить это число в системе с фиксированным числом разрядов (например, 16), нужно неиспользованные старшие разряды заполнить нулями: 00000010 00110111.

Обратный перевод осуществляется гораздо более тривиальным способом: необходимо просуммировать все цифры двоичного числа, умноженные на число 2^{номер разряда}, нумерация разрядов начинается с младшего (правого), которому соответствует номер 0. то есть:

1∙2⁹+0∙2⁸+0∙2⁷+0∙2⁶+1∙2⁵+1∙2⁴+0∙2³+1∙2²+1∙2¹+1∙2⁰=512+0+0+0+32+16+0+4+2+1=567.

Шестнадцатеричная система как удобная форма записи

Все эти вычисления занимают время и требуют большой внимательности при выполнении, поэтому использовать десятичную систему в программировании не очень удобно. Неудобно использовать также и двоичную систему из-за большого числа разрядов. Для того, чтобы представлять в удобочитаемой форме двоичные данные используется шестнадцатеричная система счисления. В ней используются цифры от 0 до 9 и латинские буквы от A до F.

010=016	810=816
110=116	910=916
210=216	1010=A16
310=316	1110=B16
410=416	1210=C16
510=516	1310=D16
610=616	1410=E16
710=716	1510=F16
810=816	1610=1016

---

Эта система счисления обладает очень важным свойством: любые четыре цифры двоичного числа (называемые тетрадой) всегда соответствуют одному шестнадцатеричному знаку:

00002=016	10002=816
00012=116	10012=916
00102=216	10102=A16
00112=316	10112=B16
01002=416	11002=C16
01012=516	11012=D16
01102=616	11102=E16
01112=716	11112=F16
10002=816	100002=1016

Поэтому совершенно тривиально осуществляется перевод из двоичной системы в шестнадцатеричную и обратно: достаточно запомнить эту таблицу, и просто заменять тетрады соответствующими знаками или наоборот. Таким образом, максимальное значение одного байта записывается как FF₁₆, а максимальное значение, с которым может работать 32-разрядный процессор без применения математического сопроцессора – FFFFFFFF₁₆.

Представление целых знаковых чисел

Прямой код


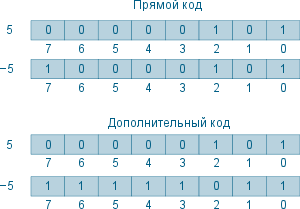
Прямой и дополнительный коды

Итак, представление целых беззнаковых чисел в двоичном коде проблемы не составляет. Возникает вопрос, что делать с целыми знаковыми числами. Первое и очевидное решение – это использовать старший бит двоичного числа для хранения знака: 0, если знак «+» и 1, если знак «−». Подобное решение называют прямым кодом. Например, для случая 8-разрядной системы, 65₁₀=01000001₂, а −65₁₀=11000001₂. Однако данная система создаёт серьёзную проблему: a−b≠a+(−b). Действительно: 00110010−00110010=0, а 00110010+10110010=11100100, что абсурдно. Значит, нужно на уровне процессора отдельно определять операции сложения и вычитания, всегда следить за тем, чтобы вычисления производились с числами одного знака. Знак же результата определять путём сравнения исходных чисел.

---

Дополнительный код

Существует другое, не вполне очевидное на первый взгляд, но очень эффективное решение – дополнительный код. Чтобы изменить знак числа в дополнительном коде, нужно выполнить такую операцию −a=ā+1, где черта над буквой – знак инверсии, замены всех нулей единицами, а единиц нулями. 65₁₀=01000001₂, а −65₁₀=10111110₂. Попробуем сложить эти два числа – получим 1 00000000₂, то есть, 256. Вспомним, однако, что мы работаем с 8-разрядной системой, а число 1 00000000₂ в ней записать невозможно. Поэтому старший бит 1 выйдет за границы числа, и в итоге останется 00000000₂, что является верным. Интересно заметить, что старший бит числа по-прежнему отвечает за знак, а потому можно использовать его значение для того, чтобы узнать знак числа. Но уже нельзя использовать простую инверсию старшего бита для смены знака. Тем не менее, такое небольшое усложнение операции смены знака ведёт к огромному упрощению остальных операций – их можно производить, не задумываясь о знаке, результат всегда будет верным.

Представление чисел с фиксированной запятой

Следующим этапом усложнения типов представляемых данных является представление десятичных дробей. Исторически первым явилось решение представлять их в формате с фиксированной запятой (точкой) ^[1]. При этом определённое количество бит числа отдаётся под целую часть, а остальные разряды – под дробную. Несложно заметить, что такое представление данных является во многом искусственным, поскольку достаточно домножить все вводимые данные на 2^{число бит дробной части}, чтобы полностью избавиться от необходимости применения записи с фиксированной запятой. К тому же, такая запись сильно ограничивает диапазон возможных значений чисел.

Представление чисел с плавающей запятой

31 30 . . . 23 22 . . . 0

---