Файл: Реферат Дисциплина Теоретические основы обеспечения надежности систем автоматизации и модулей мехатронных систем.rtf
Добавлен: 08.11.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
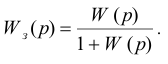
Приравняв знаменатель нулю, получим характеристическое уравнение замкнутой системы
Обозначим
Представим передаточную функцию разомкнутой системы в виде отношения двух полиномов
где
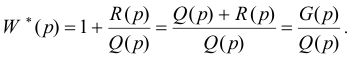
Заметим, что в этом выражении степени полиномов числителя и знаменателя одинаковы и равны
Пусть
тогда

Предположим, что разомкнутая система неустойчива и ее характеристическое уравнение имеет
Для того, чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми, то есть

Так как в соответствии с выражением (3) функции
Дадим теперь следующую формулировку критерия устойчивости Найквиста. Для того, чтобы замкнутая система была устойчивой при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФЧХ разомкнутой системы
На Рисунке 8 изображена АФЧХ устойчивой системы в замкнутом состоянии, которая в разомкнутом состоянии была неустойчива и имела два правых корня. А на рисунке 9 - АФЧХ неустойчивой системы
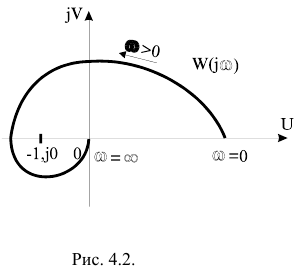
Рисунок 7
На практике обычно дается следующая формулировка критерия Найквиста. Если разомкнутая САУ устойчива, то замкнутая система будет устойчива , если АФЧХ разомкнутой системы
не охватывает точку с координатами
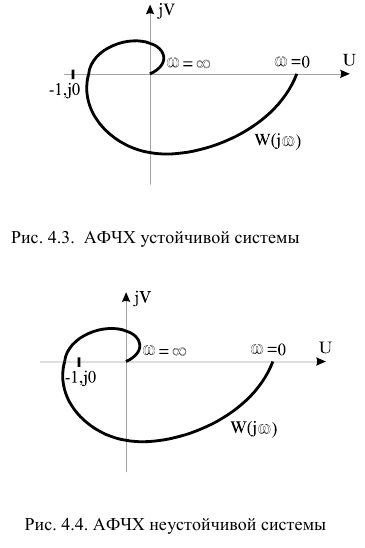
Рисунок 8

Рисунок 9
Если
Рассмотренные выше АФЧХ относятся к статическим САУ . У астатических систем, содержащих интегрирующие звенья, АФЧХ при
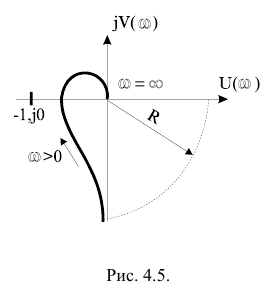
Рисунок 10
На Рисунке 10 приведена АФЧХ разомкнутой устойчивой системы с астатизмом первого порядка. Замкнутая система в этом случае также устойчива . На Рисунке 11 показана АФЧХ разомкнутой неустойчивой системы с астатизмом второго порядка . Для этого случая замкнутая система неустойчива, так как точка с координатами
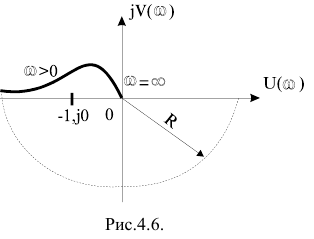
Рисунок 11
На практике широкое применение получил критерий устойчивости Найквиста с применением вместо АФЧХ логарифмических амплитудно-частотных характеристик.
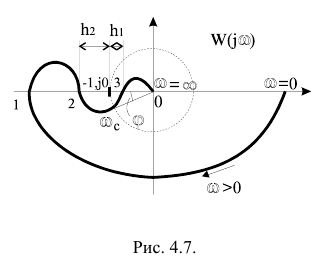
Рисунок 12
Устойчивость САУ связана с числом пересечений АФЧХ отрезка

Рисунок 13
точки
Поэтому область отрицательных ЛAЧX при исследовании устойчивости не рассматривается. Интерес представляет только область положительных ЛAЧX.
Сформулируем критерий Найквиста. Для того, чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы разность между числом положительных (на Рисунке 13 сверху вниз) и отрицательных переходов (снизу вверх) ЛЧX прямой
Если разомкнутая система устойчива, то и замкнутая система будет устойчивой (Рисунок 12 и 13), так как
.
Заключение
На практике более широкое применение, по сравнению с критерием Михайлова, нашел частотный критерий Найквиста, который позволяет судить об устойчивости замкнутой системы по частотным характеристикам этой системы в разомкнутом состоянии.
Список литературы
1. Гальперин М.В. Автоматическое управление: Учебник для студентов учреждений среднего профессионального образования.-М.: Форум: ИНФРА-М, 2010
2. Келим Ю.М. Электромеханические и магнитные элементы систем автоматики. Учебное пособие для средних профессиональных учебных заведений. 2-е изд., исправл. и доп. -М.: Высшая школа, 2009
3. Востриков А.С. Теория автоматического регулирования. Учебное пособие для вузов. 2-е изд.- М.: высшая школа, 2009.
4. Савин М.М. Теория автоматического управления. - Ростов-на-Дону: Феникс, 2010
5. Шишмарев В.Ю. Типовые элементы систем автоматического управления : учебник для студентов учреждений среднего профессионального образования. – 3-е изд. – М.: издательский центр «Академия», 2010
6. Певзнер Л.Д. Практикум по теории автоматического управления. - М.: Высшая школа, 2010
7. Никулин Е.А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем: учебное пособие для вузов.- СПБ: БХВ- Петербург, 2009