Файл: Реферат Дисциплина Теоретические основы обеспечения надежности систем автоматизации и модулей мехатронных систем.rtf

Министерство науки и высшего образования Российской Федерации

Смоленский казачий институт промышленных технологий и бизнеса (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Московский государственный университет технологий и управления имени К.Г. Разумовского

(Первый казачий университет)»

в г. Вязьме Смоленской области

Реферат

Дисциплина: «Теоретические основы обеспечения надежности систем автоматизации и модулей мехатронных систем»

Тема: «Критерии устойчивости Михайлова и Найквиста»

Направление: 15.02.07 «Автоматизация технологических процессов и производств»

Курс: САз-41(9)

Форма обучения: заочная

Студент: Райков Иван Владимирович

Преподаватель: Алекперов Закир Афтандилович

Вязьма, 2022

Оглавление

Введение

На практике более широкое применение по сравнению с критерием Михайлова получил критерий Н. Найквиста, который был разработан в 1932 г. для проверки устойчивости усилителей с отрицательной обратной связью, а затем обобщен на системы автоматического управления. Возможно, что именно этот результат послужил толчком к бурному развитию частотного метода в теории автоматического управления.

1. Исследование линейных систем на устойчивость с помощью критерия Михайлова

Критерий устойчивости Михайлова относится к частотным критериям в основе которых лежит принцип аргумента, заключающийся в следующем. Известно, что характеристический полином системы

---

может быть представлен в виде



где   — корни характеристического уравнения



Рассмотрим  -й сомножитель в (2)   и представим его на комплексной плоскости. Корень   может быть изображен в виде вектора, проведенного из начала координат в точку pj9 причем длина вектора равна его модулю, то есть  , а угол, образованный с положительным направлением действительной оси — аргументу комплексного числа   то есть   (Рисунок 1).



Рисунок 1

Аналогично на комплексной плоскости может быть изображен и вектор  , проведенный в произвольную точку этой плоскости. Тогда сомножитель   представим в виде разности двух рассмотренных векторов. В частном случае при  , где   представляет собой частоту колебаний, соответствующих мнимому корню характеристического уравнения, характеристический полином примет вид



Тогда концы векторов 

---

 будут располагаться на мнимой оси в точке   (Рисунок 2).



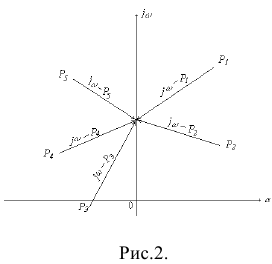
Рисунок 2

Необходимо отметить, что в (4)   представляет собой вектор, модуль которого равен



и аргумент



При изменении частоты   каждый элементарный вектор   в (4) будет поворачиваться, изменяя и модуль   в соответствии с (5) и фазу (аргумент)   в соответствии с (6). Считая поворот вектора против часовой стрелки положительным, при изменении   от   до   каждый элементарный вектор в (4) повернется на угол  , если его начало координат, то есть корень  , расположено слева от мнимой оси, и на угол  , если корень расположен справа от мнимой оси. Такой поворот элементарных векторов   изображен на Рисунке 3.



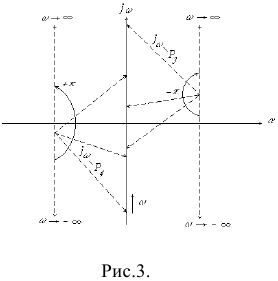
Рисунок 3

Если характеристический полином имеет   правых и 

---

 левых корней, то при изменении со от   до   вектор   повернется на угол, равный сумме поворотов элементарных векторов  , то есть изменение аргумента равно



Сформулируем принцип аргумента: изменение аргумента   при изменении частоты   от   до   равно разности между числом левых и правых корней характеристического уравнения, умноженной на  .

При изменении   от 0 до   изменение аргумента вектора   будет вдвое меньше



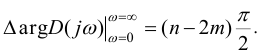
В 1936 г. на основании принципа аргумента (8) А.В. Михайловым был сформулирован следующий критерий устойчивости: для того чтобы система   — го порядка была устойчива, необходимо и достаточно, чтобы вектор  , описывающий кривую Михайлова, при изменении частоты   от 0 до   повернулся вокруг начала координат против часовой стрелки

---

, нигде не обращаясь в 0 на угол  .

Заметим, что кривая (годограф) Михайлова для устойчивых систем всегда должна начинаться на вещественной положительной полуоси, поскольку при   из (1) следует, что   на основании необходимого условия устойчивости.

Для построения кривой Михайлова необходимо представить характеристический полином в виде



где   — вещественная, а   — мнимая функции Михайлова и строить кривую Михайлова на комплексной плоскости с осью ординат   и осью абсцисс  .

Для устойчивых систем кривая Михайлова имеет плавную спиралевидную форму и уходит в бесконечность в том квадранте координатной плоскости, номер которого равен порядку характеристического уравнения. На Рисунке 4 изображены кривые Михайлова, соответствующие устойчивым системам, а на Рисунке 5 — кривые неустойчивых систем.



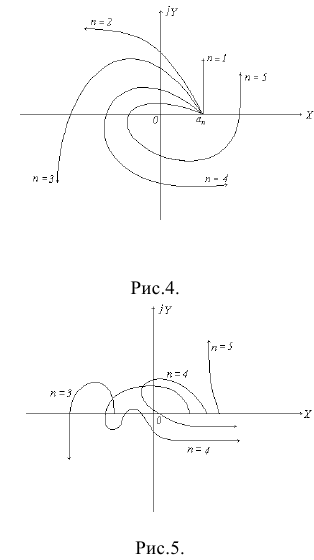
Рисунок 4



Рисунок 5

2. Исследование устойчивости САУ с помощью критерии Найквиста

Критерий Найквиста относится к частотным критериям устойчивости, был разработан американским ученым Г. Найквистом в 1932 году и позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы. Рассмотрим систему



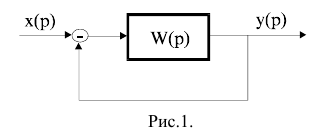
Рисунок 6

Здесь   — передаточная функция разомкнутой системы. Тогда передаточная функция замкнутой системы имеет вид

---