Файл: Практикум по программированию задач матричного исчисления. Все задачи касаются выполнения определенных действий над матрицами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 68
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №1
Задание:
Написать и отладить программу, выполняющую произведение двух матриц с комплексными коэффициентами, представленными в показательной форме записи (Aejφ).
Цель лабораторной работы
Получить навыки работы на персональной ЭВМ в среде программирования Quick Basic или Turbo Pascal, а также практикум по программированию задач матричного исчисления.
Все задачи касаются выполнения определенных действий над матрицами. Примерный список задач:
-
сложение матриц с комплексными коэффициентами; -
перемножение матриц с вещественными коэффициентами; -
перемножение матриц с комплексными коэффициентами; -
вычисление нормы матрицы; -
вычисление определителя матрицы; -
вычисление обратной матрицы; -
вычисление ранга матрицы; -
возведение матрицы в целую степень.
Краткие теоретические сведения, необходимые для решения поставленной задачи
Комплексные числа представляют собой расширение множества действительных чисел и являются суммой действительных и мнимых чисел. Мнимыми являются числа, квадрат которых отрицателен. Мнимая единица, квадрат которой дает –1, обозначается i или j. Соответственно, комплексное число Z можно представить как сумму
Z = X + jY,
где X = Re Z – действительня часть числа Z,
Y = Im Z – мнимая часть числа Z.
При этом Xи Y – действительные числа.
Существует также показательная форма записи комплексного числа
Z = Aej,
где
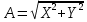 – модуль числа Z,
– модуль числа Z,φ – аргумент Z. В зависимости от знаков X и Y φ = arctg(Y/ X) или
φ = arctg(Y/ X) + π.
При этом
X = Acos φ,
Y = Asin φ.
Как мнимая, так и действительная части комплексного числа могут быть равными нулю. В первом случае (X = 0) комплексное число вырождается в чисто мнимое, во втором (Y = 0) – в действительное.
Матрица – математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы.
Пусть имеются две матрицы A и B размерности nA × mA и nB × mB (n – число строк, m – число столбцов) и с элементами aij и bij. Произведением матриц A и B называется матрица C, элементы которой равны
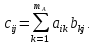
При этом необходимо, чтобы mA = nB.
Блок-схема алгоритма программы
Блок-схемы алгоритма программы и ее подпрограмм приведены на рисунках 1–5.
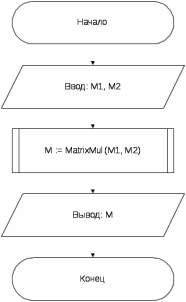
Рисунок 1 – Блок-схема алгоритма программы

Рисунок 2 – Блок-схема алгоритма подпрограммы умножения матриц с комплексными элементами

Рисунок 3 – Блок-схема алгоритма подпрограммы сложения комплексных чисел

Рисунок 4 – Блок-схема алгоритма подпрограммы сложения комплексных чисел
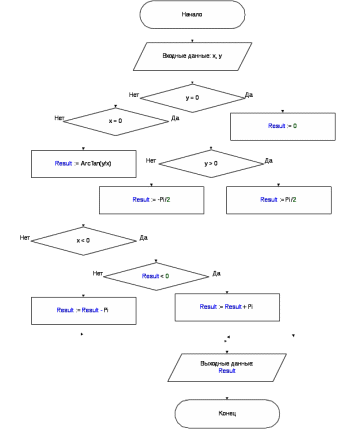
Рисунок 5 – Блок-схема алгоритма подпрограммы вычисления арктангенса с учетом знаков катетов
Текст программы
Program Lab1;
Type
// Комплексное число
Complex = record
A, // модуль
phi: Real; // аргумент
end;
// Матрица комплексных чисел
Matrix = array[,] of Complex;
// Арктангенс с учетом знаков сторон
function ArcTan(x, y: Real): Real;
begin
if y = 0 then Result := 0
else if x = 0 then
if y > 0 then Result := Pi/2
else Result := -Pi/2
else Result := ArcTan(y/x);
if x < 0 then
if Result < 0 then
Result := Result + Pi
else
Result := Result - Pi;
end;
// Сложение комплексных чисел
function ComplexPlus(C1, C2: Complex): Complex;
var x, y, x1, x2, y1, y2: Real;
begin
x1 := C1.A * cos(C1.phi);
y1 := C1.A * sin(C1.phi);
x2 := C2.A * cos(C2.phi);
y2 := C2.A * sin(C2.phi);
x := x1 + x2;
y := y1 + y2;
Result.A := sqrt(x*x + y*y);
Result.phi := arctan(x, y);
end;
// Умножение комплексных чисел
function ComplexMul(C1, C2: Complex): Complex;
begin
Result.A := C1.A * C2.A;
Result.phi := C1.Phi + C2.Phi;
end;
// Умножение матриц
function MatrixMul(M1, M2: Matrix): Matrix;
var L, L1, L2: Integer;
C: Complex;
begin
if (Length(M1, 1) <> Length(M2, 0))
then begin
writeln('Ошибка. Размерности матриц должны соответствовать.');
halt(1);
end;
L1 := Length(M1, 0);
L2 := Length(M2, 1);
L := Length(M2, 0);
SetLength(Result, L1, L2);
for var i: Integer := 0 to L1 - 1 do
for var j: Integer :=0 to L2 - 1 do begin
Result[i, j].A := 0;
Result[i, j].Phi := 0;
for var k: Integer :=0 to L-1 do begin
C := ComplexMul(M1[i, k], M2[k, j]);
Result[i, j] := ComplexPlus(Result[i, j], C);
end;
end;
end;
// Представление комплексного числа
function ComplexString(C: Complex; Len: Integer := 0): String;
begin
if C.A = 0 then Result := '0'
else begin
Result := C.A.ToString;
if C.phi <> 0 then begin
Result := Result + ' * exp(';
if C.phi < 0 then
Result := Result + '-';
Result := Result + 'j' + abs(C.phi).ToString + ')';
end;
end;
while Length(Result) < Len do Result := ' ' + Result;
end;
// Вывод комплексного числа
Procedure ComplexPrint(C: Complex; Len: Integer := 0);
begin
write(ComplexString(C, Len), #9#9);
end;
// Вывод матрицы комплексных чисел
Procedure MatrixPrint(M: Matrix);
var MaxLength: array of Integer;
Cols, L: Integer;
begin
Cols := Length(M, 1);
SetLength(MaxLength, Cols);
for var i: Integer := 0 to Cols - 1 do begin
MaxLength[i] := 0;
for var j: Integer := 0 to Length(M, 0) - 1 do begin
L := Length(ComplexString(M[j, i]));
if L > MaxLength[i] then
MaxLength[i] := L;
end;
end;
for var i: Integer := 0 to Length(M, 0) - 1 do begin
for var j: Integer := 0 to Cols - 1 do begin
ComplexPrint(M[i, j], MaxLength[j]);
Write(' ');
end;
writeln;
end;
end;
// Ввод комплексного числа
function ComplexRead: Complex;
begin
Write('Введите модуль комплексного числа: ');
Read(Result.A);
Write('Введите аргумент комплексного числа: ');
Read(Result.phi);
end;
// Ввод матрицы комплексных чисел
function MatrixRead(L1, L2: Integer): Matrix;
begin
SetLength(Result, L1, L2);
Writeln('Ввод матрицы ' + L1 + ' x ' + L2);
for var i: Integer := 1 to L1 do
for var j: Integer := 1 to L2 do begin
writeln('Ввод элемента [', i, ', ', j, ']');
Result[i-1, j-1] := ComplexRead;
end;
end;
var M1, M2, M: Matrix;
n1, n2: Integer;
begin
Writeln('Программа вычисления произведение двух матриц ' +
'с комплексными коэффициентами,');
Writeln('представленными в показательной форме записи (A exp (j phi)).');
Write('Введите число строк матрицы 1: ');
Readln(n1);
Write('Введите число столбцов матрицы 1: ');
Readln(n2);
M1 := MatrixRead(n1, n2);
Writeln('Матрица M1:');
MatrixPrint(M1);
Write('Введите число строк матрицы 2: ');
Readln(n1);
if n1 <> n2 then begin
writeln('Ошибка. Размерности матриц должны соответствовать.');
halt(1);
end;
Write('Введите число столбцов матрицы 2: ');
Readln(n2);
M2 := MatrixRead(n1, n2);
Writeln('Матрица M2:');
MatrixPrint(M2);
M := MatrixMul(M1, M2);
Writeln('Матрица M = M1 * M2:');
MatrixPrint(M);
end.
Инструкция оператору
Программа предназначена для вычисления произведение двух матриц с комплексными коэффициентами, представленными в показательной форме записи (Aejφ).
При запуске программа выдает сообщение «Программа вычисления произведение двух матриц с комплексными коэффициентами, представленными в показательной форме записи (A exp (j phi)).»
По запросу необходимо ввести перемножаемые матрицы. После ввода каждой матрицы они выводятся на экран для контроля. Затем осуществляется вычисление матриц и вывод результата.
Ввод матрицы осуществляется в следующем порядке.
-
По запросу «Введите число строк матрицы N:» необходимо ввести число строк матрицы N, где N может быть 1 или 2. -
По запросу «Введите число столбцов матрицы N:» необходимо ввести число столбцов матрицы N, где N может быть 1 или 2. -
Далее в цикле по запросам вида «Ввод элемента [i, j]» (i, j – номер строки и столбца, соответственно) осуществляется ввод комплексного элемента матрицы.
Ввод комплексного числа осуществляется в следующем порядке.
-
По запросу «Введите модуль комплексного числа» вводится модуль числа. -
По запросу «Введите аргумент комплексного числа» вводится аргумент (мнимый показатель) числа.
Контрольный пример
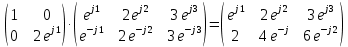
На рисунке 6 показан скриншот расчета тестового примера. Видно, что результат расчета правильный.
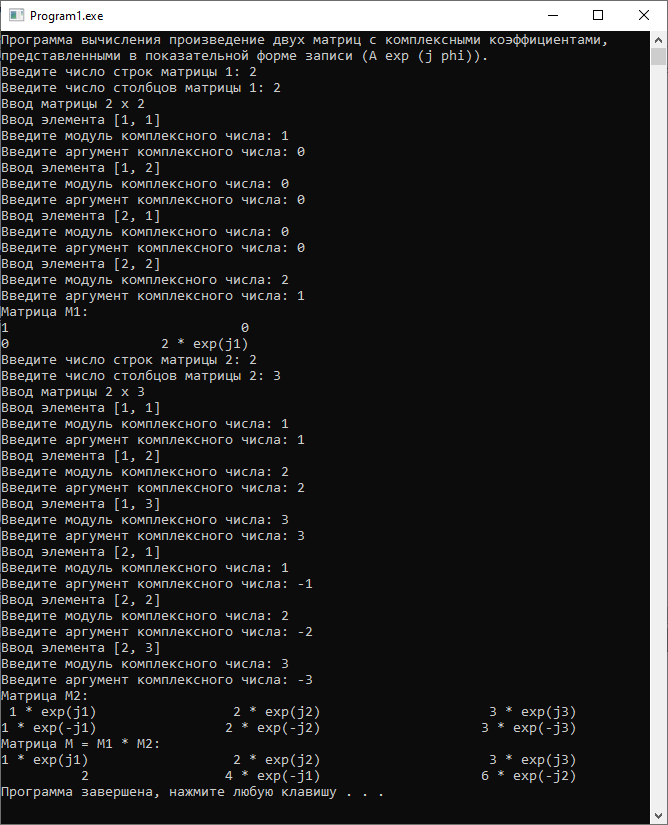
Рисунок 6 – Скриншот расчета тестового примера
Вывод
В ходе выполнения работы на языке программирования Pascal ABC написана и отлажена программа, выполняющая произведение двух матриц с комплексными коэффициентами, представленными в показательной форме записи (Aejφ). Приведены блок-схемы вычислительных алгоритмов программы, разработана инструкция оператору. Решение тестового задания подтвердило корректную работу программы.