Файл: Измерение временной сложности алгоритма в эксперименте на эвм.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 45
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра Вычислительной техники
Пояснительная записка
к курсовой работе
по дисциплине «Алгоритмы и структуры данных»
Тема: Измерение временной сложности алгоритма в эксперименте на ЭВМ
| | | |
| Студент гр. *** | | *** |
| Преподаватель | | Колинько П. Г. |
Санкт-Петербург
2023
Цель работы.
Выполнение статистического эксперимента для измерения фактической временной сложности реализованного алгоритма обработки множеств и последовательностей.
Используемая структура данных
Эксперимент проводится на дереве двоичного поиска с хранением в каждом узле мощности поддерева и с автобалансировкой, с реализованным интерфейсом для работы с множествами и последовательностями. Исследуется временная оценка выполнения следующей цепочки операций:
-
Объединение множеств -
Разность множеств -
Симметрическая разность множеств -
Слияние последовательностей (MERGE) -
Сцепление последовательностей (CONCAT) -
Включение одной последовательности в другую (SUBST)
Теоретическая оценка сложности алгоритмов
Все двуместные операции на множествах состоят из просмотра дерева за O(n) и вставку каждого элемента в результирующее дерево время за O(log n), таким образом каждая двуместная операция выполняется за O(n log n).
Операции с последовательностями имеют сложность O(n log n), так как они состоят из:
-
восстановления последовательностей – сложность O(n) -
манипуляций с последовательностями – сложность O(n log n) для операции MERGE и O(n) для CONCAT и SUBST -
преобразование последовательности (результата операции) обратно в дерево – сложность O(n log n)
В итоге, теоретической оценкой сложности выполнения всей цепочки операций над множествами и последовательностями является O(n log n).
Стратегия и результаты эксперимента
Для статистического эксперимента генерируемые значения ключей для узлов были ограничены сверху значением 1000. Было выполнено 200 испытаний с увеличением параметра входа. Мощность множеств случайно генерировалась от 9 до 28, и с каждой итерацией обе границы сдвигались на 5 (14 и 33, 19 и 38 и так далее).
Таким образом работа программы была оценена с значениями мощностей от 9 до около 1000.
Результаты эксперимента
В приложении №1 к курсовой работе приведены результаты программы за все 200 экспериментов. На рисунке 1 приведён результат статистической обработки этих данных.
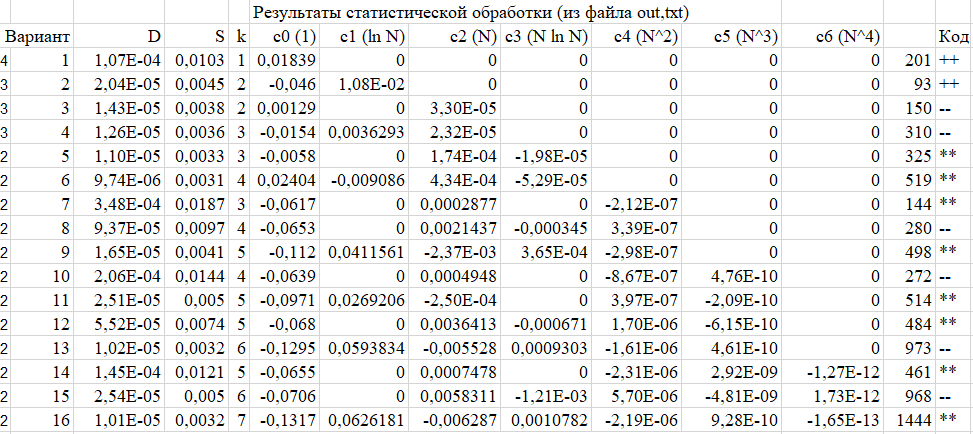
Рис. 1 Результат обработки данных
По полученным данным была составлена таблица отношений выборочной дисперсии (рис. 2) для определения подходящей модели и его регрессионного уравнения. С учётом кол-ва экспериментов квантиль Фишера = 1,26/1,39.
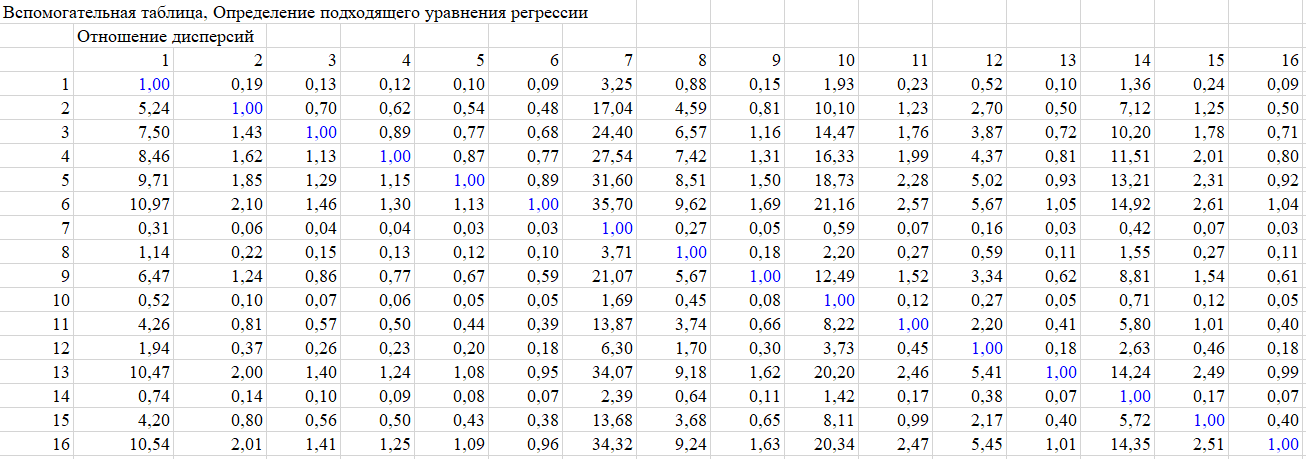
Рис. 2 Таблица отношений ВД.
Как видно из таблицы, в модели №4 отношения дисперсий перестают быть значимыми, они меньше обоих значения квантиля Фишера. Такая модель соответствует сложности O(n + ln n). Уравнение регрессии:
0,0000232296 * n + 0,00362927 * ln(n) - 0,015366
График зависимости времени от входа представлен на Рис. 3

Рис. 3 Результат статистического эксперимента.
Вывод.
При выполнении работы программа, составленная в гл. 3, была доработано таким образом, чтобы она генерировала деревья мощностью от 1 до 1000, было замерено время выполнения операций над множествами и последовательности для деревьев разной мощности и выполнен статистический эксперимент по измерению фактической временной сложности алгоритма обработки данных.
Фактической сложностью программы оказалась O(n + ln n), что отличается от теоретически расчитанной сложности программы O(n * log n).
Приложение
1 Результаты эксперимента (файл in.txt)
| 17 0,0002661 20 0,0003032 22 0,0003122 29 0,0005181 39 0,0011882 39 0,000689 47 0,0008391 46 0,0008203 58 0,001207 67 0,0014143 69 0,0014274 66 0,0014326 86 0,0020298 84 0,0019162 91 0,0020018 92 0,0020575 99 0,0028361 104 0,0027612 106 0,0024901 111 0,0027864 126 0,00324 120 0,003527 132 0,0033294 142 0,0048663 147 0,0039468 136 0,0036983 150 0,004063 151 0,0042613 168 0,004576 163 0,0047098 175 0,0056639 169 0,0051879 169 0,0062168 184 0,0056764 186 0,0056547 184 0,0055069 191 0,0052008 204 0,0062202 206 0,0065351 209 0,0063274 225 0,0080123 214 0,0088411 223 0,0077116 239 0,0081172 232 0,0073497 234 0,0077452 245 0,0078879 248 0,008614 253 0,0082032 263 0,008195 274 0,0090479 268 0,0099556 274 0,0092325 290 0,0099549 279 0,0093866 287 0,0103218 292 0,0096622 299 0,0102625 304 0,0111005 309 0,0126342 316 0,0123102 326 0,0113106 327 0,0115425 327 0,0114063 336 0,011654 340 0,0127982 341 0,0135816 352 0,0122678 366 0,0141008 356 0,0123717 375 0,013588 382 0,0135326 371 0,014042 379 0,015511 380 0,0141224 396 0,0149263 396 0,015308 396 0,0138815 401 0,0148883 421 0,0158078 419 0,0138967 414 0,0145021 435 0,0164387 433 0,0159955 431 0,0155861 436 0,0160471 452 0,0156964 450 0,0164604 453 0,0177128 466 0,0166892 475 0,0173418 476 0,0165927 488 0,0181721 489 0,017555 483 0,0175101 494 0,0203078 505 0,0257966 508 0,0253792 510 0,0181328 523 0,0338959 517 0,0250561 520 0,0307562 526 0,0301694 534 0,0278989 530 0,0272838 544 0,0252606 554 0,0200357 547 0,031186 567 0,034702 570 0,0362507 568 0,0209601 566 0,0198045 572 0,0206944 576 0,0219619 595 0,0355958 587 0,0221528 593 0,0238438 612 0,0210044 607 0,021535 604 0,0211709 622 0,0245075 625 0,0357583 622 0,0217495 631 0,0355263 647 0,0331163 651 0,0286508 653 0,0330348 659 0,0220365 668 0,02235 665 0,0231144 674 0,0233577 666 0,0223522 681 0,0252488 681 0,0238392 693 0,0242183 693 0,0247663 691 0,0233304 694 0,0230417 699 0,0235794 708 0,0235136 717 0,0239226 730 0,0263021 724 0,0254414 725 0,0239711 745 0,0269398 741 0,0253044 750 0,0243847 763 0,024829 765 0,0248065 772 0,0250612 774 0,024995 780 0,0257727 779 0,0246068 786 0,026204 787 0,0257923 801 0,0261424 793 0,0262731 796 0,0263945 799 0,0277308 817 0,0272814 828 0,0286734 832 0,028422 830 0,0270179 835 0,026817 836 0,0268274 834 0,0271135 844 0,0266082 854 0,0288528 864 0,0275984 860 0,0269271 870 0,0278064 865 0,0280509 884 0,0293477 888 0,0288502 887 0,0284124 890 0,0299705 892 0,0288325 906 0,02851 900 0,0290161 923 0,0282724 915 0,0316923 930 0,0288157 921 0,0309564 932 0,0293172 934 0,0292519 946 0,0311436 942 0,0296035 948 0,0302065 958 0,0297541 954 0,0291808 977 0,0301864 976 0,0305514 969 0,0304943 982 0,030687 981 0,0306853 994 0,0306542 996 0,0306917 999 0,0307213 1013 0,0317765 1022 0,0319445 | 17 0,0002661 20 0,0003032 22 0,0003122 29 0,0005181 39 0,0011882 39 0,000689 47 0,0008391 46 0,0008203 58 0,001207 67 0,0014143 69 0,0014274 66 0,0014326 86 0,0020298 84 0,0019162 91 0,0020018 92 0,0020575 99 0,0028361 104 0,0027612 106 0,0024901 111 0,0027864 126 0,00324 120 0,003527 132 0,0033294 142 0,0048663 147 0,0039468 136 0,0036983 150 0,004063 151 0,0042613 168 0,004576 163 0,0047098 175 0,0056639 169 0,0051879 169 0,0062168 184 0,0056764 186 0,0056547 184 0,0055069 191 0,0052008 204 0,0062202 206 0,0065351 209 0,0063274 225 0,0080123 214 0,0088411 223 0,0077116 239 0,0081172 232 0,0073497 234 0,0077452 245 0,0078879 248 0,008614 253 0,0082032 263 0,008195 274 0,0090479 268 0,0099556 274 0,0092325 290 0,0099549 279 0,0093866 287 0,0103218 292 0,0096622 299 0,0102625 304 0,0111005 309 0,0126342 316 0,0123102 326 0,0113106 327 0,0115425 327 0,0114063 336 0,011654 340 0,0127982 341 0,0135816 352 0,0122678 366 0,0141008 356 0,0123717 375 0,013588 382 0,0135326 371 0,014042 379 0,015511 380 0,0141224 396 0,0149263 396 0,015308 396 0,0138815 401 0,0148883 421 0,0158078 419 0,0138967 414 0,0145021 435 0,0164387 433 0,0159955 431 0,0155861 436 0,0160471 452 0,0156964 450 0,0164604 453 0,0177128 466 0,0166892 475 0,0173418 476 0,0165927 488 0,0181721 489 0,017555 483 0,0175101 494 0,0203078 505 0,0257966 508 0,0253792 510 0,0181328 523 0,0338959 517 0,0250561 520 0,0307562 526 0,0301694 534 0,0278989 530 0,0272838 544 0,0252606 554 0,0200357 547 0,031186 567 0,034702 570 0,0362507 568 0,0209601 566 0,0198045 572 0,0206944 576 0,0219619 595 0,0355958 587 0,0221528 593 0,0238438 612 0,0210044 607 0,021535 604 0,0211709 622 0,0245075 625 0,0357583 622 0,0217495 631 0,0355263 647 0,0331163 651 0,0286508 653 0,0330348 659 0,0220365 668 0,02235 665 0,0231144 674 0,0233577 666 0,0223522 681 0,0252488 681 0,0238392 693 0,0242183 693 0,0247663 691 0,0233304 694 0,0230417 699 0,0235794 708 0,0235136 717 0,0239226 730 0,0263021 724 0,0254414 725 0,0239711 745 0,0269398 741 0,0253044 750 0,0243847 763 0,024829 765 0,0248065 772 0,0250612 774 0,024995 780 0,0257727 779 0,0246068 786 0,026204 787 0,0257923 801 0,0261424 793 0,0262731 796 0,0263945 799 0,0277308 817 0,0272814 828 0,0286734 832 0,028422 830 0,0270179 835 0,026817 836 0,0268274 834 0,0271135 844 0,0266082 854 0,0288528 864 0,0275984 860 0,0269271 870 0,0278064 865 0,0280509 884 0,0293477 888 0,0288502 887 0,0284124 890 0,0299705 892 0,0288325 906 0,02851 900 0,0290161 923 0,0282724 915 0,0316923 930 0,0288157 921 0,0309564 932 0,0293172 934 0,0292519 946 0,0311436 942 0,0296035 948 0,0302065 958 0,0297541 954 0,0291808 977 0,0301864 976 0,0305514 969 0,0304943 982 0,030687 981 0,0306853 994 0,0306542 996 0,0306917 999 0,0307213 1013 0,0317765 1022 0,0319445 | 17 0,0002661 20 0,0003032 22 0,0003122 29 0,0005181 39 0,0011882 39 0,000689 47 0,0008391 46 0,0008203 58 0,001207 67 0,0014143 69 0,0014274 66 0,0014326 86 0,0020298 84 0,0019162 91 0,0020018 92 0,0020575 99 0,0028361 104 0,0027612 106 0,0024901 111 0,0027864 126 0,00324 120 0,003527 132 0,0033294 142 0,0048663 147 0,0039468 136 0,0036983 150 0,004063 151 0,0042613 168 0,004576 163 0,0047098 175 0,0056639 169 0,0051879 169 0,0062168 184 0,0056764 186 0,0056547 184 0,0055069 191 0,0052008 204 0,0062202 206 0,0065351 209 0,0063274 225 0,0080123 214 0,0088411 223 0,0077116 239 0,0081172 232 0,0073497 234 0,0077452 245 0,0078879 248 0,008614 253 0,0082032 263 0,008195 274 0,0090479 268 0,0099556 274 0,0092325 290 0,0099549 279 0,0093866 287 0,0103218 292 0,0096622 299 0,0102625 304 0,0111005 309 0,0126342 316 0,0123102 326 0,0113106 327 0,0115425 327 0,0114063 336 0,011654 340 0,0127982 341 0,0135816 352 0,0122678 366 0,0141008 356 0,0123717 375 0,013588 382 0,0135326 371 0,014042 379 0,015511 380 0,0141224 396 0,0149263 396 0,015308 396 0,0138815 401 0,0148883 421 0,0158078 419 0,0138967 414 0,0145021 435 0,0164387 433 0,0159955 431 0,0155861 436 0,0160471 452 0,0156964 450 0,0164604 453 0,0177128 466 0,0166892 475 0,0173418 476 0,0165927 488 0,0181721 489 0,017555 483 0,0175101 494 0,0203078 505 0,0257966 508 0,0253792 510 0,0181328 523 0,0338959 517 0,0250561 520 0,0307562 526 0,0301694 534 0,0278989 530 0,0272838 544 0,0252606 554 0,0200357 547 0,031186 567 0,034702 570 0,0362507 568 0,0209601 566 0,0198045 572 0,0206944 576 0,0219619 595 0,0355958 587 0,0221528 593 0,0238438 612 0,0210044 607 0,021535 604 0,0211709 622 0,0245075 625 0,0357583 622 0,0217495 631 0,0355263 647 0,0331163 651 0,0286508 653 0,0330348 659 0,0220365 668 0,02235 665 0,0231144 674 0,0233577 666 0,0223522 681 0,0252488 681 0,0238392 693 0,0242183 693 0,0247663 691 0,0233304 694 0,0230417 699 0,0235794 708 0,0235136 717 0,0239226 730 0,0263021 724 0,0254414 725 0,0239711 745 0,0269398 741 0,0253044 750 0,0243847 763 0,024829 765 0,0248065 772 0,0250612 774 0,024995 780 0,0257727 779 0,0246068 786 0,026204 787 0,0257923 801 0,0261424 793 0,0262731 796 0,0263945 799 0,0277308 817 0,0272814 828 0,0286734 832 0,028422 830 0,0270179 835 0,026817 836 0,0268274 834 0,0271135 844 0,0266082 854 0,0288528 864 0,0275984 860 0,0269271 870 0,0278064 865 0,0280509 884 0,0293477 888 0,0288502 887 0,0284124 890 0,0299705 892 0,0288325 906 0,02851 900 0,0290161 923 0,0282724 915 0,0316923 930 0,0288157 921 0,0309564 932 0,0293172 934 0,0292519 946 0,0311436 942 0,0296035 948 0,0302065 958 0,0297541 954 0,0291808 977 0,0301864 976 0,0305514 969 0,0304943 982 0,030687 981 0,0306853 994 0,0306542 996 0,0306917 999 0,0307213 1013 0,0317765 1022 0,0319445 | 17 0,0002661 20 0,0003032 22 0,0003122 29 0,0005181 39 0,0011882 39 0,000689 47 0,0008391 46 0,0008203 58 0,001207 67 0,0014143 69 0,0014274 66 0,0014326 86 0,0020298 84 0,0019162 91 0,0020018 92 0,0020575 99 0,0028361 104 0,0027612 106 0,0024901 111 0,0027864 126 0,00324 120 0,003527 132 0,0033294 142 0,0048663 147 0,0039468 136 0,0036983 150 0,004063 151 0,0042613 168 0,004576 163 0,0047098 175 0,0056639 169 0,0051879 169 0,0062168 184 0,0056764 186 0,0056547 184 0,0055069 191 0,0052008 204 0,0062202 206 0,0065351 209 0,0063274 225 0,0080123 214 0,0088411 223 0,0077116 239 0,0081172 232 0,0073497 234 0,0077452 245 0,0078879 248 0,008614 253 0,0082032 263 0,008195 274 0,0090479 268 0,0099556 274 0,0092325 290 0,0099549 279 0,0093866 287 0,0103218 292 0,0096622 299 0,0102625 304 0,0111005 309 0,0126342 316 0,0123102 326 0,0113106 327 0,0115425 327 0,0114063 336 0,011654 340 0,0127982 341 0,0135816 352 0,0122678 366 0,0141008 356 0,0123717 375 0,013588 382 0,0135326 371 0,014042 379 0,015511 380 0,0141224 396 0,0149263 396 0,015308 396 0,0138815 401 0,0148883 421 0,0158078 419 0,0138967 414 0,0145021 435 0,0164387 433 0,0159955 431 0,0155861 436 0,0160471 452 0,0156964 450 0,0164604 453 0,0177128 466 0,0166892 475 0,0173418 476 0,0165927 488 0,0181721 489 0,017555 483 0,0175101 494 0,0203078 505 0,0257966 508 0,0253792 510 0,0181328 523 0,0338959 517 0,0250561 520 0,0307562 526 0,0301694 534 0,0278989 530 0,0272838 544 0,0252606 554 0,0200357 547 0,031186 567 0,034702 570 0,0362507 568 0,0209601 566 0,0198045 572 0,0206944 576 0,0219619 595 0,0355958 587 0,0221528 593 0,0238438 612 0,0210044 607 0,021535 604 0,0211709 622 0,0245075 625 0,0357583 622 0,0217495 631 0,0355263 647 0,0331163 651 0,0286508 653 0,0330348 659 0,0220365 668 0,02235 665 0,0231144 674 0,0233577 666 0,0223522 681 0,0252488 681 0,0238392 693 0,0242183 693 0,0247663 691 0,0233304 694 0,0230417 699 0,0235794 708 0,0235136 717 0,0239226 730 0,0263021 724 0,0254414 725 0,0239711 745 0,0269398 741 0,0253044 750 0,0243847 763 0,024829 765 0,0248065 772 0,0250612 774 0,024995 780 0,0257727 779 0,0246068 786 0,026204 787 0,0257923 801 0,0261424 793 0,0262731 796 0,0263945 799 0,0277308 817 0,0272814 828 0,0286734 832 0,028422 830 0,0270179 835 0,026817 836 0,0268274 834 0,0271135 844 0,0266082 854 0,0288528 864 0,0275984 860 0,0269271 870 0,0278064 865 0,0280509 884 0,0293477 888 0,0288502 887 0,0284124 890 0,0299705 892 0,0288325 906 0,02851 900 0,0290161 923 0,0282724 915 0,0316923 930 0,0288157 921 0,0309564 932 0,0293172 934 0,0292519 946 0,0311436 942 0,0296035 948 0,0302065 958 0,0297541 954 0,0291808 977 0,0301864 976 0,0305514 969 0,0304943 982 0,030687 981 0,0306853 994 0,0306542 996 0,0306917 999 0,0307213 1013 0,0317765 1022 0,0319445 | 17 0,0002661 20 0,0003032 22 0,0003122 29 0,0005181 39 0,0011882 39 0,000689 47 0,0008391 46 0,0008203 58 0,001207 67 0,0014143 69 0,0014274 66 0,0014326 86 0,0020298 84 0,0019162 91 0,0020018 92 0,0020575 99 0,0028361 104 0,0027612 106 0,0024901 111 0,0027864 126 0,00324 120 0,003527 132 0,0033294 142 0,0048663 147 0,0039468 136 0,0036983 150 0,004063 151 0,0042613 168 0,004576 163 0,0047098 175 0,0056639 169 0,0051879 169 0,0062168 184 0,0056764 186 0,0056547 184 0,0055069 191 0,0052008 204 0,0062202 206 0,0065351 209 0,0063274 225 0,0080123 214 0,0088411 223 0,0077116 239 0,0081172 232 0,0073497 234 0,0077452 245 0,0078879 248 0,008614 253 0,0082032 263 0,008195 274 0,0090479 268 0,0099556 274 0,0092325 290 0,0099549 279 0,0093866 287 0,0103218 292 0,0096622 299 0,0102625 304 0,0111005 309 0,0126342 316 0,0123102 326 0,0113106 327 0,0115425 327 0,0114063 336 0,011654 340 0,0127982 341 0,0135816 352 0,0122678 366 0,0141008 356 0,0123717 375 0,013588 382 0,0135326 371 0,014042 379 0,015511 380 0,0141224 396 0,0149263 396 0,015308 396 0,0138815 401 0,0148883 421 0,0158078 419 0,0138967 414 0,0145021 435 0,0164387 433 0,0159955 431 0,0155861 436 0,0160471 452 0,0156964 450 0,0164604 453 0,0177128 466 0,0166892 475 0,0173418 476 0,0165927 488 0,0181721 489 0,017555 483 0,0175101 494 0,0203078 505 0,0257966 508 0,0253792 510 0,0181328 523 0,0338959 517 0,0250561 520 0,0307562 526 0,0301694 534 0,0278989 530 0,0272838 544 0,0252606 554 0,0200357 547 0,031186 567 0,034702 570 0,0362507 568 0,0209601 566 0,0198045 572 0,0206944 576 0,0219619 595 0,0355958 587 0,0221528 593 0,0238438 612 0,0210044 607 0,021535 604 0,0211709 622 0,0245075 625 0,0357583 622 0,0217495 631 0,0355263 647 0,0331163 651 0,0286508 653 0,0330348 659 0,0220365 668 0,02235 665 0,0231144 674 0,0233577 666 0,0223522 681 0,0252488 681 0,0238392 693 0,0242183 693 0,0247663 691 0,0233304 694 0,0230417 699 0,0235794 708 0,0235136 717 0,0239226 730 0,0263021 724 0,0254414 725 0,0239711 745 0,0269398 741 0,0253044 750 0,0243847 763 0,024829 765 0,0248065 772 0,0250612 774 0,024995 780 0,0257727 779 0,0246068 786 0,026204 787 0,0257923 801 0,0261424 793 0,0262731 796 0,0263945 799 0,0277308 817 0,0272814 828 0,0286734 832 0,028422 830 0,0270179 835 0,026817 836 0,0268274 834 0,0271135 844 0,0266082 854 0,0288528 864 0,0275984 860 0,0269271 870 0,0278064 865 0,0280509 884 0,0293477 888 0,0288502 887 0,0284124 890 0,0299705 892 0,0288325 906 0,02851 900 0,0290161 923 0,0282724 915 0,0316923 930 0,0288157 921 0,0309564 932 0,0293172 934 0,0292519 946 0,0311436 942 0,0296035 948 0,0302065 958 0,0297541 954 0,0291808 977 0,0301864 976 0,0305514 969 0,0304943 982 0,030687 981 0,0306853 994 0,0306542 996 0,0306917 999 0,0307213 1013 0,0317765 1022 0,0319445 |