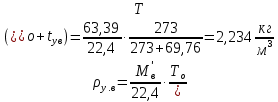ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 270
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3. РАСЧЁТ РЕКТИФИКАЦИОННОЙ КОЛОННЫ
3.1. Материальный баланс процесса массообмена
3.2. Определение минимального флегмового числа
3.3. Определение условно – оптимального флегмового числа
3.4. Расчёт средних массовых потоков жидкости и пара
3.5. Расчёт максимально допустимой скорости пара и диаметра колонны
3.7. Расчет гидравлического сопротивления колонны
4. РАСЧЁТ ВСПОМОГАТЕЛЬНОГО ОБОРУДОВАНИЯ
4.2. Расчёт диаметров трубопроводов
4.4. Подбор ёмкостей для сбора продуктов и хранения сырья
4.5. Подбор конденсатоотводчиков
3.2. Определение минимального флегмового числа
Для смеси ацетон-толуол (Методическое пособие ПАХТ) выписываем равновесные составы жидкости и пара при 760 мм.рт.ст.
| x, мол. доли | y, мол. доли | t,°С |
| 0 | 0 | 109,9216 |
| 0,006726 | 0,052556 | 108,1663 |
| 0,013883 | 0,105056 | 106,3609 |
| 0,021633 | 0,157471 | 104,4885 |
| 0,030171 | 0,209764 | 102,5331 |
| 0,039723 | 0,26188 | 100,4809 |
| 0,050326 | 0,313794 | 98,33786 |
| 0,062353 | 0,365396 | 96,08464 |
| 0,076 | 0,416593 | 93,72164 |
| 0,091505 | 0,467259 | 91,24972 |
| 0,109611 | 0,517054 | 88,65198 |
| 0,130706 | 0,565659 | 85,94443 |
| 0,155584 | 0,61244 | 83,1452 |
| 0,18471 | 0,656701 | 80,30371 |
| 0,218577 | 0,69745 | 77,49444 |
| 0,257108 | 0,73382 | 74,81411 |
| 0,299716 | 0,765316 | 72,35319 |
| 0,345482 | 0,792015 | 70,16746 |
| 0,393469 | 0,81448 | 68,26808 |
| 0,442929 | 0,833484 | 66,63434 |
| 0,493322 | 0,849852 | 65,22637 |
| 0,544299 | 0,864303 | 64,00229 |
| 0,595624 | 0,877459 | 62,92234 |
| 0,647136 | 0,889865 | 61,95172 |
| 0,698708 | 0,902019 | 61,06067 |
| 0,750225 | 0,914408 | 60,22508 |
| 0,801557 | 0,927537 | 59,42653 |
| 0,852538 | 0,941972 | 58,65265 |
| 0,902922 | 0,958369 | 57,89809 |
| 0,95234 | 0,977482 | 57,16623 |
| 1 | 1 | 56,47439 |
Построим равновесную кривую между жидкостью и паром. На построенной фазовой диаграмме проведем диагональ квадрата.
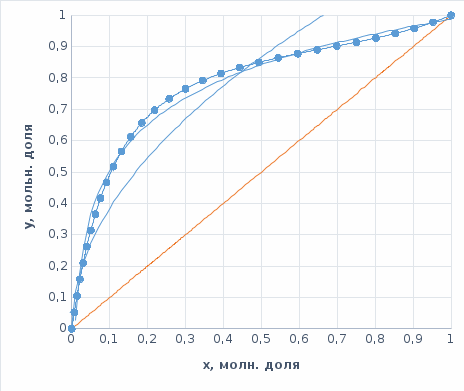
Рис.1 Х-У диаграмма смеси ацетон-толуол
Минимальное флегмовое число определяется уравнением:
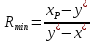
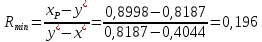
3.3. Определение условно – оптимального флегмового числа
При определении условно - оптимального флегмового числа R, учитывающего оптимизацию затрат задаются различными значениями
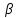 (избытка флегмы), рассчитывают уравнения рабочих линий колонны, производят их построение на Y-X-диаграмме и определяют фактор затрат, равный
(избытка флегмы), рассчитывают уравнения рабочих линий колонны, производят их построение на Y-X-диаграмме и определяют фактор затрат, равный 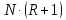 , где
, где 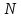 – число теоретических тарелок колонны. По зависимости
– число теоретических тарелок колонны. По зависимости 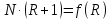 определяют оптимальные значения коэффициента β и числа R.
определяют оптимальные значения коэффициента β и числа R.Зададимся различными значениями коэффициента избытка флегмы и определим соответствующие флегмовые числа по формуле:
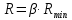
По формуле 7.6 [2, стр. 320] запишем уравнение рабочей линии верхней
(укрепляющей) части колонны:
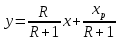
Отложив на оси ординат свободный член
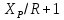 , наносим рабочую линию для верхней (укрепляющей) части колонны. Через точку (Xw; Yw) и точку пересечения линии питания и рабочей линии для укрепляющей части колонны (точка питания) проводим рабочую линию для исчерпывающей части колонны.
, наносим рабочую линию для верхней (укрепляющей) части колонны. Через точку (Xw; Yw) и точку пересечения линии питания и рабочей линии для укрепляющей части колонны (точка питания) проводим рабочую линию для исчерпывающей части колонны.Графическим построением ступеней изменения концентраций между равновесной и рабочими линиями на диаграмме Х-Y находим N. Для нахождения условно-оптимального флегмового числа определим минимальное произведение N(R+1) пропорциональное объёму ректификационной колонны (N - число ступеней изменения концентраций или теоретических тарелок, определяющее высоту колонны, а (R+1) - расход пара и, следовательно, сечение колонны). По результатам расчётов оптимальное значение коэффициента избытка флегмы составило
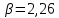 .
. 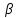 | R | N | N(R+1) |
| 1,30 | 6,95 | 0,25 | 8,7 |
| 1,40 | 6,59 | 0,27 | 8,4 |
| 1,50 | 6,01 | 0,29 | 7,8 |
| 1,60 | 5,95 | 0,31 | 7,8 |
| 1,70 | 5,88 | 0,33 | 7,8 |
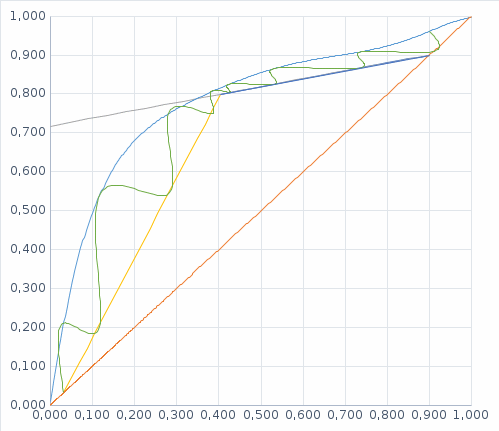
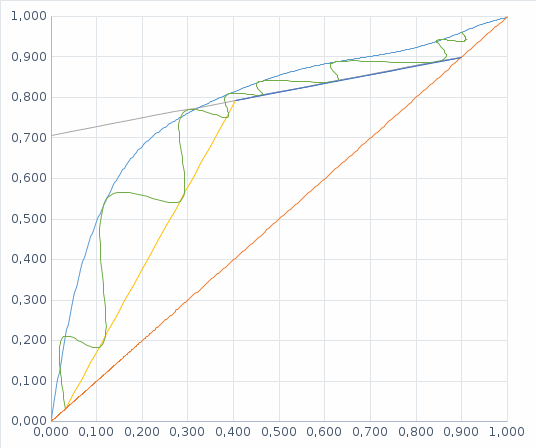
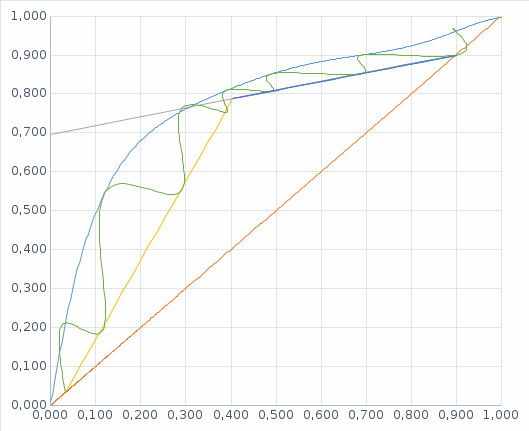
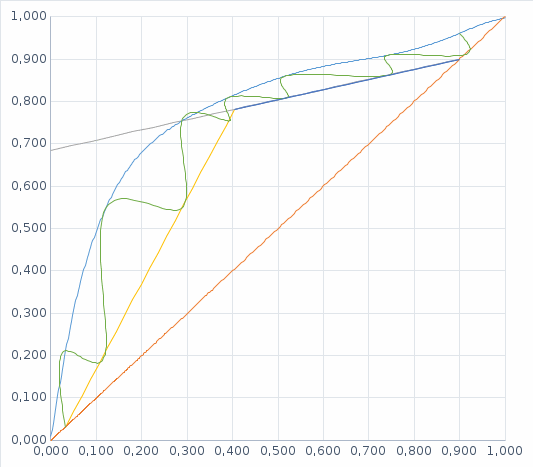
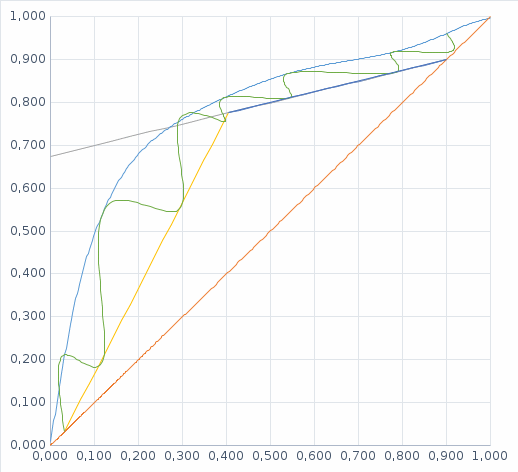
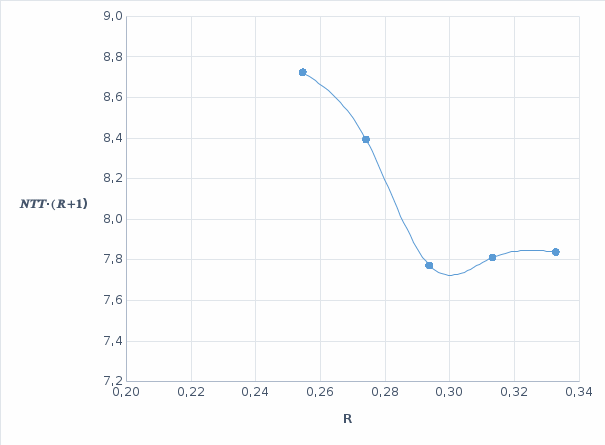
Рис 2. Определение оптимального флегмового числа
Минимальное произведение N(R+1) соответствует R = 0,293.
3.4. Расчёт средних массовых потоков жидкости и пара
Определим средний мольный состав жидкости соответственно в верхней и нижней части колонны:
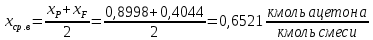
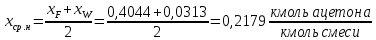
Средний массовый состав жидкости:

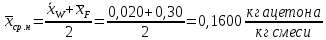
Средние мольные массы жидкости в верхней и нижней части колонны определим по формуле 6.6 [3, стр. 230]:
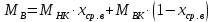
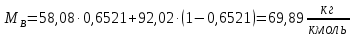
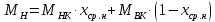
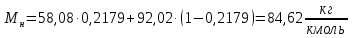
Средние массовые расходы по жидкости для верхней и нижней части колонны определим по формуле 6.4-6.5 [3, стр. 229]:
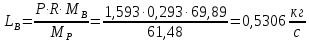
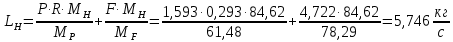
Определим средний мольный состав пара соответственно в верхней и нижней части колонны:
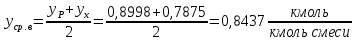
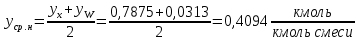
Средние мольные массы паров в верхней и нижней части колонны определим по формуле 6.8 [3, стр. 230]:
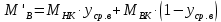
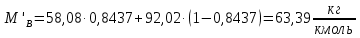
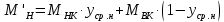
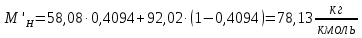
Средние массовые потоки пара в верхней и нижней части колонны определим по формуле 6.7 [3, стр. 230]
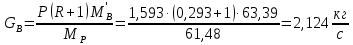
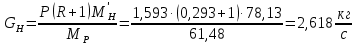
3.4.1. Расчет физико-химических свойств
Средние температуры жидкости определим по диаграмме t-(x,y) [1]:
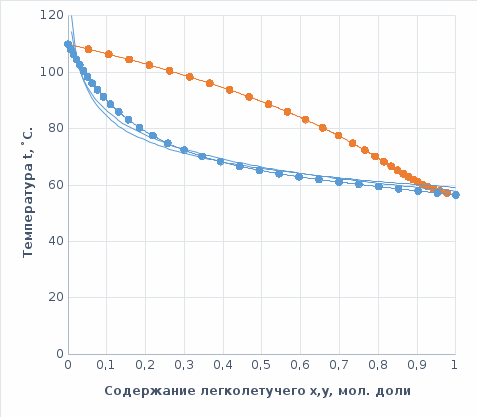
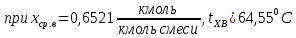
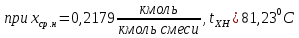
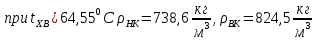
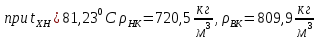
Плотность жидких смесей определим по формуле 1.3 [2, стр. 12]
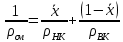
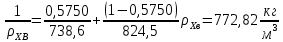
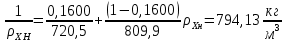
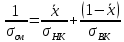
Определим поверхностное натяжение жидкости в верхней и нижней части колонны
Поверхностное натяжение [10] при температурах:
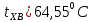
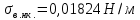
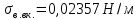
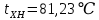
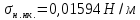
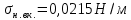
Для верхней части колонны:
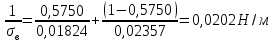
Для нижней части колонны:
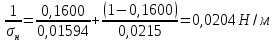
Определим вязкость жидкости по формуле 1.14 [2, стр. 15]:
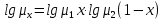
Для верхней части колонны:
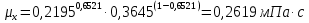
Для нижней части колонны:
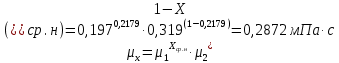
Средние температуры паров определим по диаграмме t–(x,y) [1, стр. 644]:
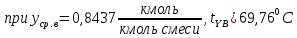
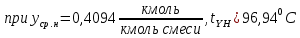
Плотность пара в верхней и нижней части колонны определим по уравнению Клапейрона (формула 1.5 [2, стр. 13]) с учетом того, что
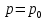 :
: