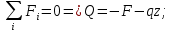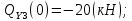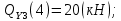Файл: Расчет нагрузок несущих конструкций.docx

АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ОБРАЗОВАНИЯ.

МЕЖДУНАРОДНЫЙ ИНСТИТУТ КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
КУРСОВАЯ РАБОТА
по дисциплине «Прикладная механика»

Тема: «Расчет нагрузок несущих конструкций»

Выполнил: студент группы АСПо-211

Сиротин Роман Владимирович

Проверил: доцент кафедры ЕН и ГД

Окрачков А.А.
Дата: 17.05.2023

Подпись: ___________________


ВОРОНЕЖ

2023
Содержание

1. Построение эпюр при растяжении и сжатии

Стальной двухступенчатый брус (рис 1.) нагружен силами: 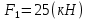, , 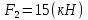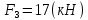. Площади поперечных сечений: 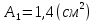, 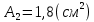; модуль упругости материала 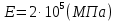. Построить эпюры продольных сил и нормальных напряжений по длине бруса, а также эпюру перемещений поперечных сечений бруса.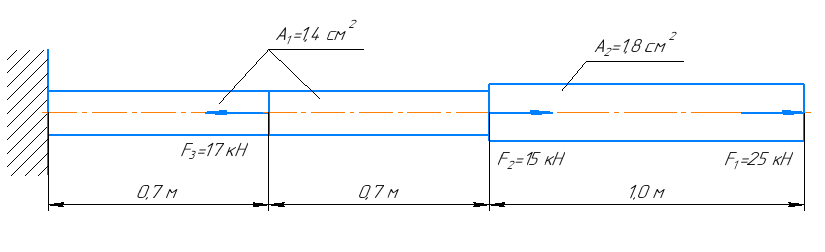



Рисунок 1 – Расчетная схема бруса

Разбиваем брус на участки. Границами участков являются сечения, в которых приложены действующие внешние силы, а также места изменения поперечного сечения бруса. В данном случае имеется три участка, которые номеруются справа-налево (от свободного конца балки). С помощью метода сечений определяем продольные силы N на каждом участке.

Участок 1.

Рассекаем брус на две части, так чтобы сечение находилось в пределах первого участка, и рассмотрим равновесие правой части бруса.

---

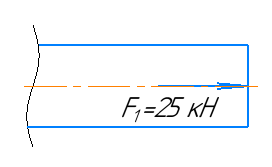
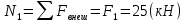
Участок 2.

Рассекаем брус на две части сечением, находящимся в пределах второго участка.





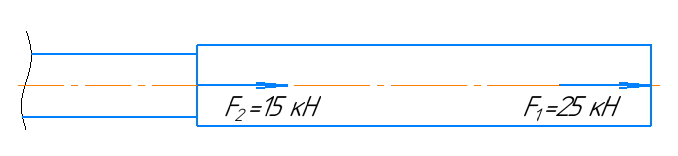
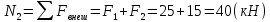
Участок 3.

Рассекаем брус на две части сечением, находящимся в пределах третьего участка, и рассмотрим равновесие правой части бруса.

П 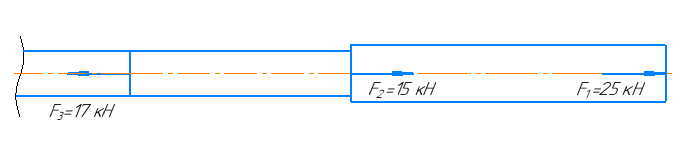равило знаков для продольной силы при растяжении (сжатии):
Если внешняя сила направлена от сечения продольная сила берется со знаком (+). Если внешняя сила направлена к сечению, то продольная сила N берется со знаком (-). При этом (+) соответствует растяжению, а (-) сжатию.



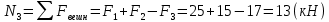
Эпюра продольной силы приведена на рисунке 2.

Рассчитываем величины нормальных напряжений δ по формуле:

,

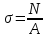где А – площадь поперечного сечения бруса.

Участок 1:

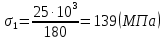
Участок 2:

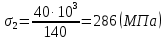
Участок 3:

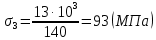
Определяем удлинения участок бруса по формуле:

,

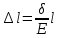где l–первоначальная длина соответствующего участка.

Участок 1:

Участок 2:

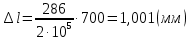
Участок 3:

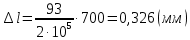
Строим эпюры продольной силы, нормального напряжения и перемещений (рисунок 2).


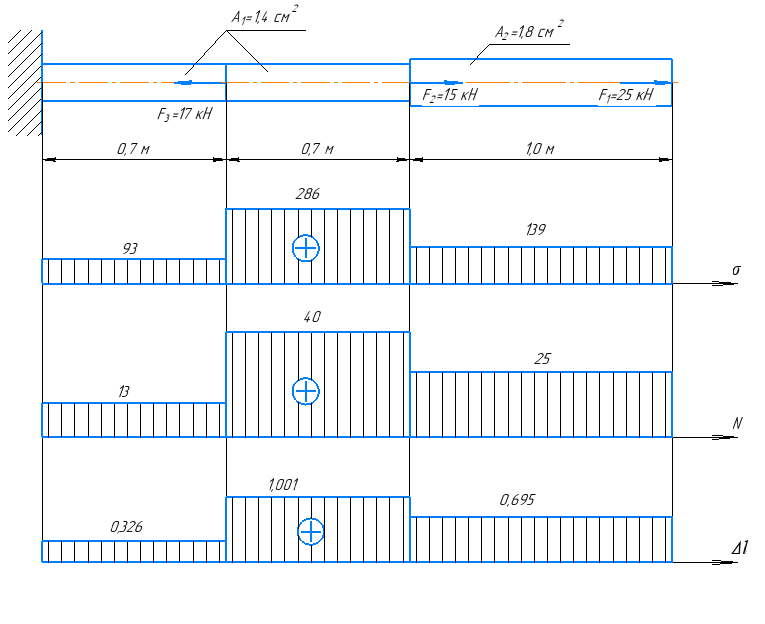
Рисунок 2 – Эпюры бруса

2. Расчет вала круглого поперечного сечения на прочность и жесткость.

Даны крутящие моменты мощности

---

угловая скорость вращения вала 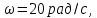допустимый угол закручивания 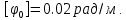Материал вала – сталь, допустимое касательное напряжение при кручении 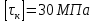, модуль сдвига 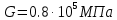. Определить диаметр вала из расчета на прочность и жесткость. Расчетная схема представлена на рис 3.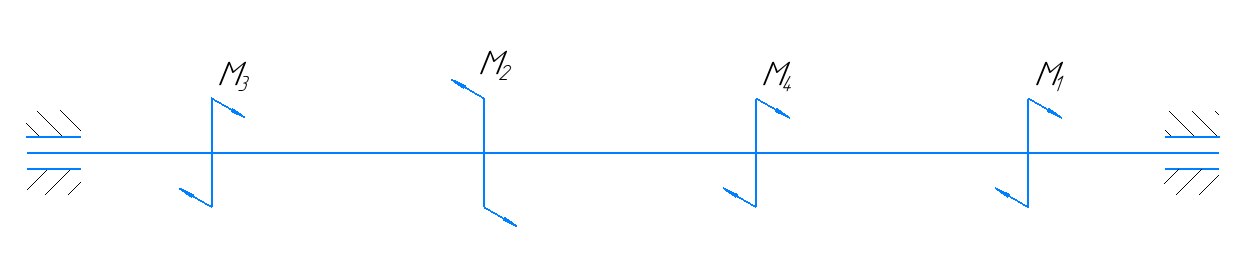



Рисунок 3 – Расчетная схема вала

Крутящий момент мощности и угловая скорость вала определяется по формуле:

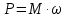
Поэтому:







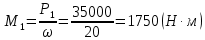
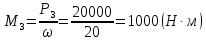
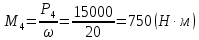
Рассмотрим динамические равновесия вала:





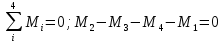
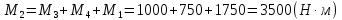
Разбиваем вал на 5 участков и рассматриваем равновесие.

Участок 1.

Рассекаем вал на две части так, чтобы сечение находилось в пределах первого участка, и рассматриваем равновесие левой части:






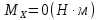
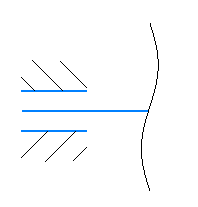
Участок 2.

Рассекаем вал на две части так, чтобы сечение находилось в пределах первого участка, и рассматриваем равновесие левой части:






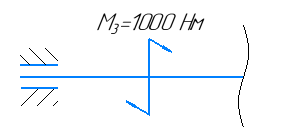
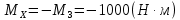
Участок 3.

Рассекаем вал на две части так, чтобы сечение находилось в пределах первого участка, и рассматриваем равновесие левой части:

---

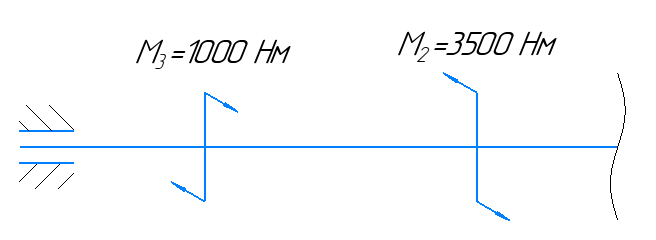
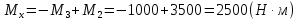
Участок 4.

Рассекаем вал на две части так, чтобы сечение находилось в пределах первого участка, и рассматриваем равновесие левой части:





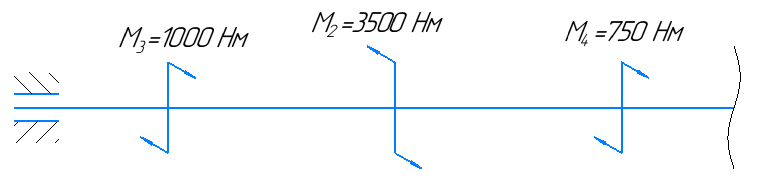
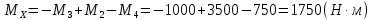
Участок 5.

Р ассекаем пятый участок и рассматриваем его правую часть:



Эпюра крутящего момента 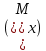, построенная по результатам расчетов, представлена на рисунке 4.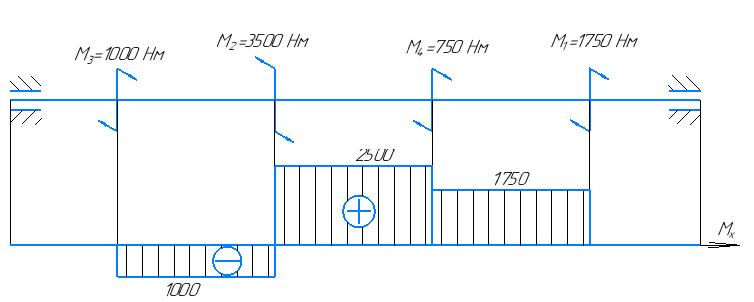



Рисунок 4 – Эпюра крутящего момента

Определяем диаметр вала из расчета на прочность и жесткость.

Условие жесткости записывается в виде:
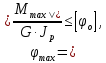
где 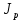- полярный момент инерции поперечного сечения вала.

Для вала круглого поперечного сечения он определяется следующим образом:

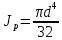
Следовательно:



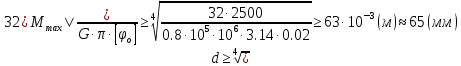
Условие прочности записывается в виде:
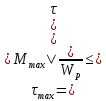
где 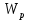– полярный момент сопротивления поперечного сечения вала.

Для круглого поперечного сечения 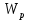определяется следующим образом: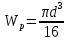

Следовательно:



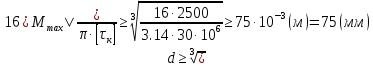
Таким образом, диаметр вала, который обеспечивает необходимую прочность и жесткость при данном распределении крутящих моментов, равен 75 мм.

3.Расчет консольной балки на прочность.

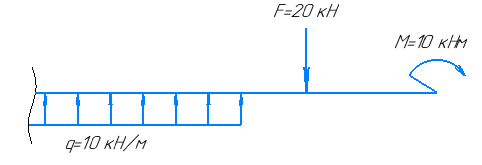
Рассматриваемая балка представлена на рисунке 5. Даны исходные данные:


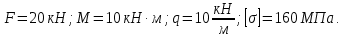
Произвести расчет нагрузки на балку для вариантов балки:

1. 
   Поперечное сечение балки в виде прямоугольника ( );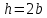
   
2. 
   Поперечное сечение в виде двутавра.
   

---

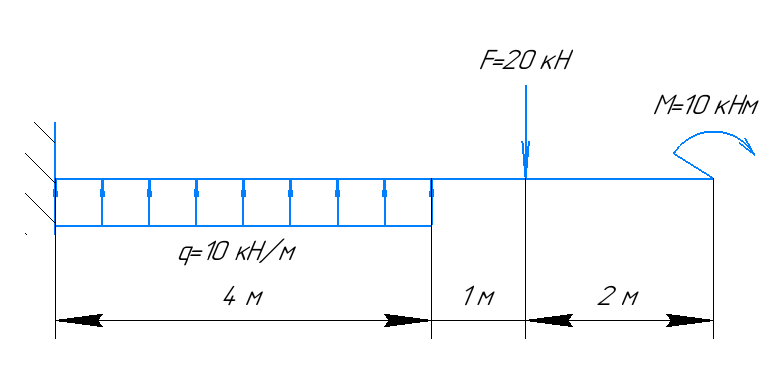
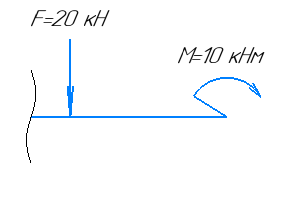
Рисунок 5 – Расчетная схема балки

Разбиваем балку на участки, используем метод сечений. Границами участков являются сечения, в которых приложена внешняя нагрузка. Рассчитываем на каждом участке величины силы 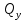и изгибающих моментов 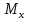. Нумерацию участков производим справа налево.

Правило знаков для построения эпюр при изгибе:

• 
  Для изгибающих моментов: если равнодействующая внешних сил пытается загнуть свободный конец балки вверх, относительно сечения, то изгибающий момент считается положительным, если вниз, то отрицательным
  
• 
  Для поперечной силы: внешние силы, поворачивающие рассматриваемую часть балки относительно сечения по часовой стрелке, соответствуют положительным значениям поперечной силы, против часовой стрелки – отрицательным.
  

Участок 1. (0≤Z≤2)

Рассекаем на две части, так чтобы сечение находилось на расстоянии Х от правого конца балки. Рассматриваем условия равновесия правой части балки.







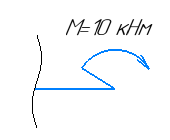
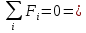
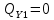
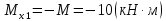
Участок 2. (0≤Z≤1)

Рассекаем балку на две части, так чтобы сечения находились в пределах второго участка.











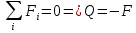
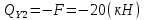
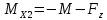
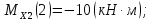
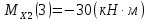
Участок 3. (0≤Z≤4)

---