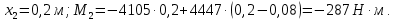ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 75
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
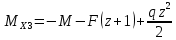
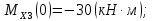
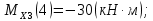
Правило знаков для распределенной нагрузки при построении эпюры моментов приведено на рисунке 6.
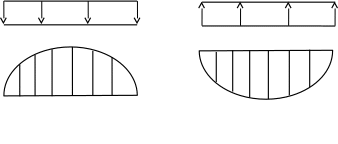
Рис 6.
Зависимость Mz(x) квадратичная.
Для нахождения точки экстремума используется условие равенства нулю производной от функции Mz(x):
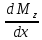 =0
=0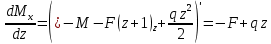 ;
;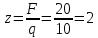 (м);
(м);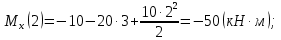
Эпюры поперечных сил и изгибающих моментов приведены на рисунке 7.
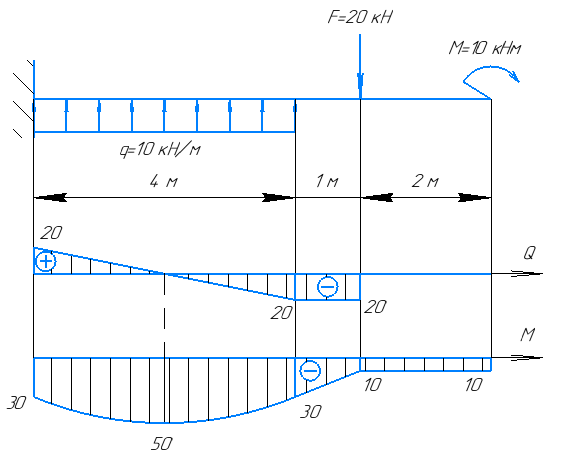
Рисунок 7 – Эпюры внутренних усилий
Определяем необходимые размеры поперечного сечения балки из расчета на прочность.
Условие прочности при изгибе балок из пластичных материалов записывается в виде:
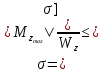
Следовательно:
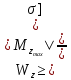
-
Поперечное сечение в виде прямоугольника
Для прямоугольника справедливо:
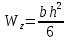 . C учетом того, что
. C учетом того, что  :
: 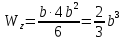
Таким образом:
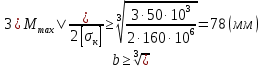
Окончательно принимаем
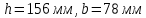
-
Параллельное сечение в виде двутавра.
Все параметры двутавров приведены в ГОСТе, поэтому выбираем требуемый двутавр, соответствующий требуемому моменту сопротивления.
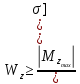
В соответствии с ГОСТ 8239-72 выбирается двутавр номер 27, у которого
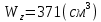
Площадь поперечного сечения в случае использования прямоугольного сечения составляет:
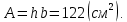
Площадь поперечного сечения двутавра номер 27:
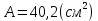 (ГОСТ 8239-72)
(ГОСТ 8239-72)Таким образом, расход материала в случае использования двутавра в 3 раза меньше.
4.Расчет двухопорной балки на прочность
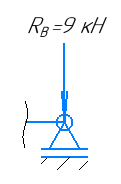
На рисунке 8 изображена двухопорная балка. Определить реакции опор, построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения из условия прочности.
Рассмотреть два варианта:
-
поперечное сечение в виде прямоугольника -
поперечное сечение в виде круга с диаметром d.
Сравнить варианты по расходу материала. В расчётах принять: [σ]=150(МПа), F1=20 (кH), F2=10 (кH), M=12 (кH
 м)
м)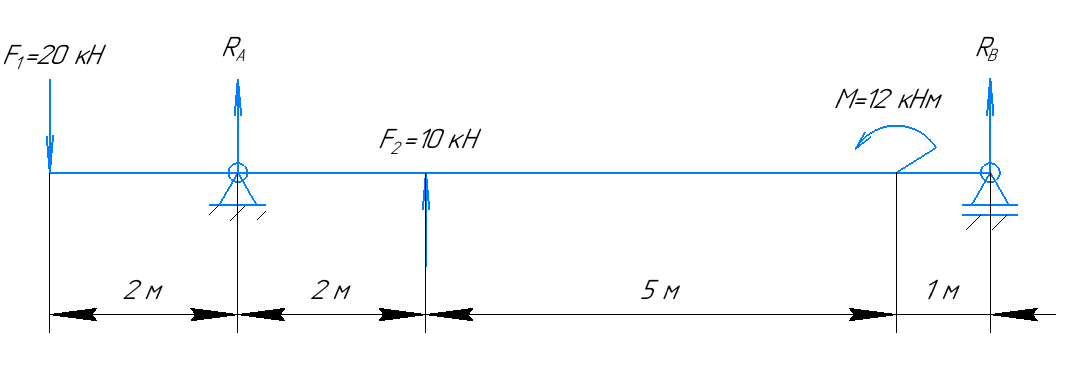
Рисунок 8 – Расчетная схема балки
Определяем реакции опор. Объект равновесия – вся балка.
Записываем условие равновесия:
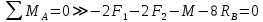
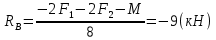
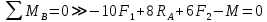
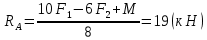
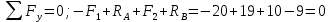
Разбиваем балку на участки, границами участков являются сечения, в которых приложена внешняя нагрузка. С помощью метода сечений найдём величину поперечной силы QY и изгибающий момент MZ на каждом участке
Участок 1.
Рассекаем балку так, чтобы сечение находилось в пределах 1-го участка, на расстоянии X от правого края балки. При условии
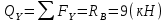
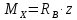
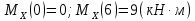
Участок 2.
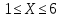
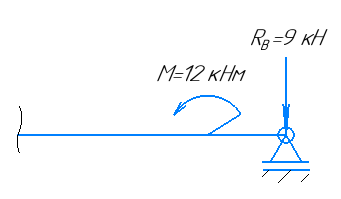
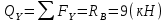
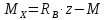
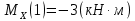
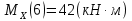
Участок 3.
Рассекаем балку так, чтобы сечение находилось в пределах 3-го участка, на расстоянии X от правого края балки. При условии:
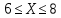

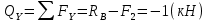
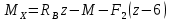
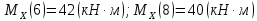
Участок 4.
Рассекаем балку так, чтобы сечение находилось в пределах 4-го участка, на расстоянии X от левого края балки. При условии:
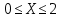
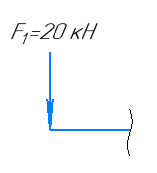
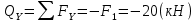
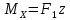
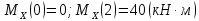
Эпюры поперечных сил и изгибающих моментов выглядят следующим образом:
Рисунок 9 – Эпюры внутренних усилий
Определяем необходимые размеры поперечного сечения балки из расчёта на прочность. Условие прочности при изгибе балок из пластичных материалов определяется:

Следовательно:

-
Поперечное сечение в виде прямоугольника h=2b.
Для прямоугольника справедливо:
 . С учетом того, что
. С учетом того, что  :
: 
Таким образом:
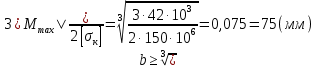
Окончательно принимаем b=75(мм); h=150(мм). При этом площадь поперечного сечения равняется: S=11250(мм2).
-
Сечение в виде круга с диаметром d. Для круга: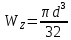
Откуда следует:
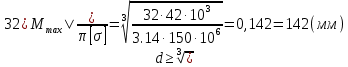
Окончательно принимаем d=145(мм). При этом площадь поперечного сечения S=228(мм2).
Таким образом, при использовании сечения балки в виде прямоугольника расход материала примерно в 49 раза выше.
5.Расчет бруса круглого поперечного сечения на изгиб с кручением
Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами (рисунок 10), передающего мощность
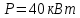 , при угловой скорости
, при угловой скорости 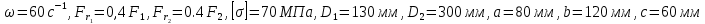 . Рассчитать диаметр, исходя из условия прочности.
. Рассчитать диаметр, исходя из условия прочности.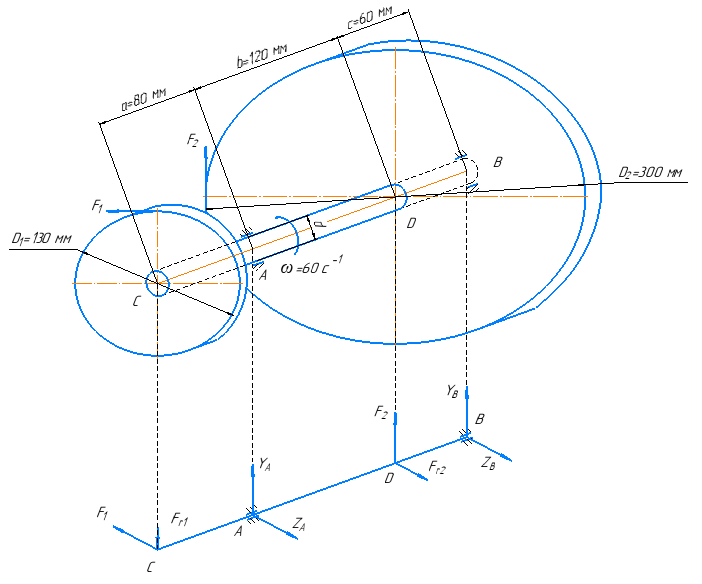
Рисунок 10 – Расчетная схема вала
Расчетная схема вала составлена при условии того, что действующая нагрузка приведена к оси вала.
При этом учтены следующие свойства сил:
-
Сила есть скользящий вектор, следовательно, силы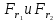 перенесены вдоль линий действия и приложены к оси.
перенесены вдоль линий действия и приложены к оси. -
При параллельном переносе силы добавлена “присоединяющая” пара сил, момент которой равен моменту силы относительно новой точки приложения. Поэтому при переносе сил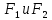 на ось вала, добавлены пары сил, моменты которых соответственно равны:
на ось вала, добавлены пары сил, моменты которых соответственно равны: 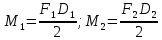
Данные моменты характеризуют вращательное действие на вал со стороны зубчатых колес, при этом
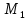 является движущим моментом (его направление совпадает с направлением вращения вала), а
является движущим моментом (его направление совпадает с направлением вращения вала), а 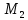 – момент сопротивления.
– момент сопротивления.Реакция подшипников А и В обозначены
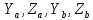 соответственно. Величины и направления реакции опор неизвестны, поэтому они указаны в произвольных направлениях (в положительных направлениях осей Y и Z).
соответственно. Величины и направления реакции опор неизвестны, поэтому они указаны в произвольных направлениях (в положительных направлениях осей Y и Z).Определяем вращающий момент, действующий на вал. Так как вал вращается с постоянной скоростью, то движущий момент
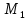 уравновешивается моментом сопротивления
уравновешивается моментом сопротивления 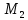
.
Передаваемая валом мощность и момент связаны соотношением:
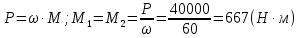
Рассчитываем величины сил, действующих на вал:
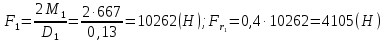
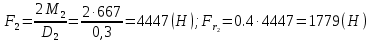
Определяем реакции опор. Расчетную схему вала будем рассматривать в вертикальной и горизонтальной плоскостях раздельно.
Расчетная схема вала в вертикальной плоскости представлена на рисунке 11.

Рисунок 11 – Расчетная схема вала в вертикальной плоскости
Для определения реакции опоры
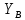 воспользуемся условием равновесия:
воспользуемся условием равновесия: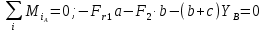
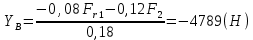
Для определения реакции опоры
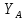 воспользуемся условием равновесия:
воспользуемся условием равновесия: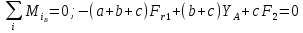
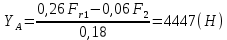
Проверка:
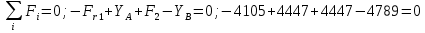
Для построения эпюр в вертикальной плоскости рассчитываем поперечные силы и изгибающие моменты, при этом разбиваем вал на три участка слева - направо. При проведении сечения первого участка рассматриваем левую часть вала. При проведении сечения третьего участка, рассматриваем правую часть вала.
Участок 1: 0≤
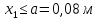
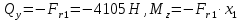
при
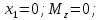
при
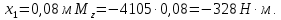
Участок 2: 0,08 м ≤
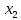 ≤
≤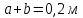
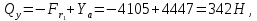
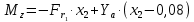
при
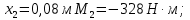
при