Файл: Джеймс Максвелл.docx

где 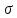– электропроводность среды.
Видно, что уравнения Максвелла – это дифференциальные уравнения в частных производных по времени и координатам, так как операторы векторного анализа , и др. – пространственные производные.
Надо заметить, что уравнения (3) и (4) – это теорема Остроградского Гаусса для электрической и магнитной 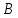индукций. Поэтому их можно объединить в одно: [2]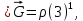



где 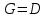при или при .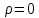
В этом случае вместо четырех уравнений будет три: (1), (2), (3).

Кроме того, уравнения (3) и (4) есть основание рассматривать как следствие уравнений (1) и (2). Действительно, если из (1) и (2) взять дивергенцию, а затем проинтегрировать по времени и учесть для (1) уравнение непрерывности, а для (2) факт, то получим (3) и (4). Поэтому можно считать два первых уравнения Максвелла основными, а остальные – вспомогательными.

Любая задача электродинамики решается с помощью уравнений Максвелла и использования граничных и начальных условий. Кстати, граничные условия получены тоже с помощью уравнений Максвелла. Они – основа волновой оптики. С их участием удалось количественно подтвердить волновой принцип Гюйгенса, сформулированный ученым еще 1,5 века тому назад. Хотя в природе и нет магнитных зарядов и токов, но замкнутая рамка с электрическим током эквивалентна магнитному диполю, перпендикулярному плоскости рамки. Эта эквивалентность имеет место на расстояниях много больших размеров рамки. В свою очередь магнитный диполь эквивалентен элементу проводника с магнитным током. Так появляются магнитные заряды и токи, которые со знаком «минус» вводят в уравнения (2) и (4) соответственно. [3]

Теперь уравнения Максвелла стали симметричными. При этом отдельно их составляют для магнитных зарядов и токов. Потом получая нужные характеристики, в частности граничные условия. Из них следует, что

---

можно представить плотностью электрического тока, а 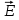– плотностью магнитного тока. Тогда любая точка пространства с радиоволнами, характеризуемая вектором Пойтинга, эквивалентна двум диполям Герца – электрическому и магнитному, которые взаимно перпендикулярны и служат источником вторичных радиоволн, распространяющихся в направлении вектора Пойтинга. [1]

Диаграмма направленности такого источника является однонаправленной в виде кардиоиды, что и подтверждает принцип Гюйгенса количественно. В теории антенн рассматривается не точка, а бесконечно малая площадка с вектором Пойтинга, называемая элементом Гюйгенса. Это – основа расчёта рупорных и других поверхностных антенн, хотя и нет в природе магнитных зарядов и токов. И тут ещё один элемент диалектики. [3]

Уравнения Максвелла позволяют получить теорию цепей. Тем не менее теория с самого начала завоёвывала свои позиции с большим трудом, поскольку к ней относились скептически многие учёные того времени и вот почему.

Тогда господствовал принцип относительности Галилея – один из важнейших законов всей классической физики. Уравнения, не изменяющиеся при преобразовании Галилея, называются инвариантными, и они справедливы, как, например, уравнения механики Ньютона. Уравнения Максвелла – не инвариантны относительно преобразований Галилея, что и было основанием для скептицизма. [1]

Физики XIX века вслед за Максвеллом считали, что электромагнитные волны распространяются в особой среде, подобно тому, как звуковые волны распространяются в воздухе. Поэтому предполагали, что уравнения Максвелла справедливы в координатной системе, связанной с эфиром. В связи с этим надо было установить, увлекается ли эфир движущимися в нём телами или остаётся неподвижным относительно абсолютно покоящегося пустого пространства.

Опыт Майкельсона показал, что наблюдения не только над механическими, но и электромагнитными явлениями, производимыми внутри системы тел, не могут обнаружить её поступательного равномерного движения. Поэтому принципы относительности и постоянства скорости света послужили исходными положениями для построения частной теории относительности, которая начинается с преобразований Лоренца, переходящих при малых скоростях в преобразования Галилея. Свои открытия голландец сделал при изучении трансформационных свойств уравнений Максвелла, поэтому они инвариантны относительно преобразований Лоренца. [3]

---

Заключение

Поправка Максвелла – основа его уравнений – получена в результате обобщения закона Ампера на случай переменных токов с учетом закона сохранения заряда и теоремы Остроградского-Гаусса. Первое и второе уравнения Максвелла являются основными.

Уравнения Максвелла явились мощным толчком к созданию и обоснованию теории относительности, одной из самых значимых теорий XX века. Она исходит из того, что для распространения света (электромагнитных волн) не требуется никакой материальной светоносной среды (эфира), свет может распространяться даже в вакууме.

Заметим, что в истории физики стык XIX и XX веков был самым продуктивным, весьма богатым на открытия и изобретения. Сюда можно отнести и другие области физики, которыми занимался Максвелл, давая очень плодотворные результаты. В кинетическую теорию им были введены «распределение Максвелла» и «статистика Максвелла-Больцмана», изобретён «диск Максвелла». Он нашёл термодинамический парадокс, много лет не дававший покоя физикам – «дьявол Максвелла». Его перу принадлежат изящные исследования по устойчивости колец Сатурна, за что он получил академическую медаль и стал признанным лидером математических физиков.

Кроме того, Максвелл создал множество небольших шедевров на самые разнообразные темы – от осуществления первой в мире цветной фотографии до разработки способа радикального выведения с одежды жирных пятен.

Но главная память о Максвелле, вероятно, единственном в истории человеке, в честь которого наука зафиксировала столько именных названий: «уравнения Максвелла», «электродинамика Максвелла», «поправка Максвелла», «ток Максвелла» и, помимо прочего, «максвелл» – единица магнитного потока в системе CGS.

Список использованных источников

1. Бордонская Л.А., Серебрякова С.С. К 150-летию создания Джеймсом Клерком Максвеллом теории электромагнитного поля. // Ученые записки Забайкальского государственного университета. - 2015. № 3 (62). - С. 143-148.

2. Волков А.А. Истоки и величие уравнений максвелла. // Мир транспорта. - 2011. Т. 9. № 2 (35). - С. 176-182.

3. Гуслякова О.И., Левин Ю.И. Джеймс Клерк Максвелл: две знаменательные даты. // Известия высших учебных заведений. Прикладная нелинейная динамика. - 2014. Т. 22. № 6. - С. 108-126.

4. Томилин К.А. Уравнения электродинамики у ДЖ.К. Максвелла и Г. Герца. // В сборнике: Исследования по истории физики и механики 2016-2018. Институт истории естествознания и техники им. С.И. Вавилова РАН. Москва. - 2019. - С. 481-515.

---