Добавлен: 24.11.2023
Просмотров: 84
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Петербургский государственный университет путей сообщения
Императора Александра I»
(ФГБОУ ВО ПГУПС)
Факультет «Автоматизация и интеллектуальные технологии»
Кафедра «Автоматика и телемеханика на железных дорогах»
Специальность 23.05.05 Системы обеспечения движения поездов
Специализация Автоматика и телемеханика на железнодорожном транспорте
КУРСОВАЯ РАБОТА
по дисциплине «Основы теории надежности"
на тему: «Методы расчета показателей надежности СЖАТ»
| Обучающийся Курс V Группа | подпись, дата | |
| Руководитель | подпись, дата | |
Санкт-Петербург
2023

Оглавление
1. Особенности надежности и безопасности СЖАТ 3
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем 5
3. Методы расчета показателей надежности СЖАТ 6
3.1 Статистические оценки показателей надежности 6
3.2 Расчет надежности комбинационных схем 15
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов 20
3.6 Расчет эксплуатационной надежности СЖАТ 31
4. Выводы об особенностях применения и эффективности использования различных методов при расчетах надежности СЖАТ 40
5. Способы повышения надежности и безопасности устройств и систем ЖАТ 43
Заключение 45
Литература 47
1. Особенности надежности и безопасности СЖАТ
При разработке и обслуживании в процессе эксплуатации систем автоматики, телемеханики и связи инженер должен обеспечивать выполнение алгоритма функционирования и определённый уровень надёжности.
Надёжность важнейшая характеристика любого технического объекта, от которой зависит целесообразность его использования по назначению. При разработке и внедрении новой аппаратуры обычно определяют показатели её надёжности.
Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонта, хранения и транспортирования.
Надёжность объекта оценивается не только во время непосредственной эксплуатации, но и во время хранения, транспортировки и ремонта. Поэтому надёжность является сложным свойством и состоит из сочетания следующих свойств: безотказности, долговечности, ремонтопригодности и сохраняемости.
Надежность связана со всеми этапами проектирования, изготовления и использования изделия. Каждый из этих этапов вносит свою лепту в решение трудной задачи создание изделия требуемого уровня надёжности с наименьшими затратами времени и средств. При проектировании и расчёте изделия закладывается его надёжность. Она зависит от конструкции, применяемых материалов, методов защиты от различных вредных воздействий, системы смазки, приспособленности к ремонтам и обслуживанию и других конструктивных особенностей.
При изготовлении изделия обеспечивается его надёжность. Она зависит от качества изготовленных деталей, методов контроля выпускаемой продукции, возможностей управления ходом технологического процесса, от качества сборки изделия и его узлов, методов испытания готовой продукции и других показателей технологического процесса.
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
Показателями надежности называются количественные характеристики одного или нескольких свойств, составляющих надежность системы. Выбор тех или иных показателей продиктован видом исследуемой системы. В теории надежности различают восстанавливаемые и невосстанавливаемые системы. К невосстанавливаемым относят системы, восстановление которых непосредственно после отказа считается нецелесообразным или невозможным, а к восстанавливаемым – в которых проводится восстановление непосредственно после отказа.
Показателями надежности восстанавливаемых систем являются: функция готовности, коэффициент готовности, наработка на отказ, параметр потока отказов.
К показателям надежности невосстанавливаемых систем
относятся: интегральный закон распределения времени безотказной работы; интегральный закон распределения времени до отказа; дифференциальный закон распределения времени исправной работы устройства до первого отказа; среднее время безотказной работы (средняя наработка до отказа); интенсивность отказов.
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.1.1 Построение функции распределения и функции плотности распределения по статистической выборке
На основании статистической выборки из 30 значений построить гистограмму частот. Используя критерий Пирсона, убедиться в экспоненциальном законе распределения времени наработки до отказа t. Построить теоретическую функцию плотности распределения a(t).
| № варианта | Статистическая выборка времени наработки до отказа T, дней | ||||||||||||||
| 18 | 1034 | 2283 | 2472 | 945 | 107 | 15 | 3803 | 235 | 3699 | 2350 | 5466 | 1506 | 851 | 788 | 2762 |
| 21 | 3011 | 1977 | 532 | 263 | 4359 | 3415 | 641 | 1126 | 5887 | 2199 | 162 | 811 | 1754 | 1040 | 111 |
Переведем время наработки до отказа в часы, в результате статистика примет следующий вид (таблица 1.1). (*24)
Таблица 1.1
| № варианта | Статистическая выборка времени наработки до отказа T, ч | ||||||||||||||
| 18 | 24816 | 54792 | 59328 | 22680 | 2568 | 360 | 91272 | 5640 | 88776 | 56400 | 131184 | 36144 | 20424 | 18912 | 66288 |
| 21 | 72264 | 47448 | 12768 | 6312 | 104616 | 81960 | 15384 | 27024 | 141288 | 52776 | 3888 | 19464 | 42096 | 24960 | 2664 |
Статистический ряд для данной выборки, а также номер интервала, в который попадает определенное значение представлены в таблице 2.
Таблица 2
| 360 | 2568 | 2664 | 3888 | 5640 | 6312 | 12768 | 15384 | 18912 | 19464 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 |
| 20424 | 22680 | 24816 | 24960 | 27024 | 36144 | 42096 | 47448 | 52776 | 54792 |
| 2 | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 |
| 56400 | 59328 | 66288 | 72264 | 81960 | 88776 | 91272 | 104616 | 131184 | 141288 |
| 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 10 | 10 |
Возьмем диапазон значений случайной величины от 360 до 141288.
Диапазон значений случайной величины t:
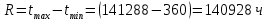
Количество интервалов K:
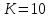
Интервал
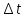
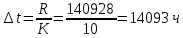
Частота попадания в i-й интервал
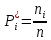
1.
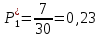
2.
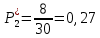
3.
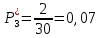
4.
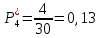
5.
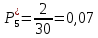
6.