Файл: Федеральное государственное казенное общеобразовательное.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 107
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тип урока: комплексное применение знаний.
Основное содержание темы, понятия, термины показательная функция, показательные неравенства.
Оборудование: проектор, интерактивная доска, презентация, карточки с заданиями.
| | Этапы работы | Содержание | этапа |
| Деятельность преподавателя | Деятельность обучающихся | ||
| 1. | Организационный момент, включающий:
| ||
| 2. | Устная работа | Проводит опрос кадет: | Вступают в диалог, отвечают |
| |
| 1.Какую функцию называют показательной? | на вопросы. |
| |
| 2.Какие типы показательных неравенств вы знаете? | |
| |
опроса. |
| |
| 3. | Повторение и обобщение теоретического материала
| При решении показательныx неравенств используются следующие утверждения:
Аналогично, аf x < аg x равносильно f(x) < g(x).
аf(x) > аg(x) равносильно неравенству f(x) Аналогично, аf x < аg x равносильно f(x) > g(x).
равносильно совокупности систем | Фиксируют информацию в тетрадях и устной речи. |
| | | неравенств h(x) > 1, f(x) > g(x), 0 < h(x) < 1, f(x) < g(x). | |
| 4. | Закрепление учебного материала
нового учебного материала; | Приводит примеры решения тестовых задач и критерии оценивания (приложение 1) Организует работу в группах по закреплению решения показательных неравенств. | Обсуждают решение заданий. Работают в группах по 3-4 человека. Решают задания (приложение 2) |
| 6. | Задание на дом. | | |
Приложение 1
-
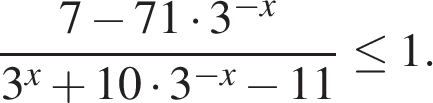 Решите неравенство
Решите неравенство
Решение.
Пусть
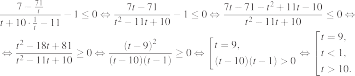
Перейдем к переменной x.
Итак, искомые значения х:
О т в е т :
-
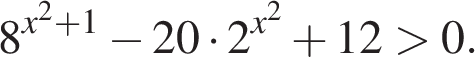 Решите неравенство
Решите неравенство
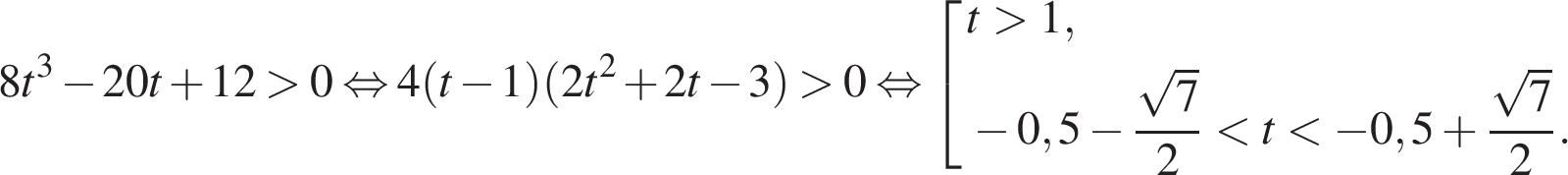 Пусть тогда
Пусть тогдаВернемся к исходной переменной:
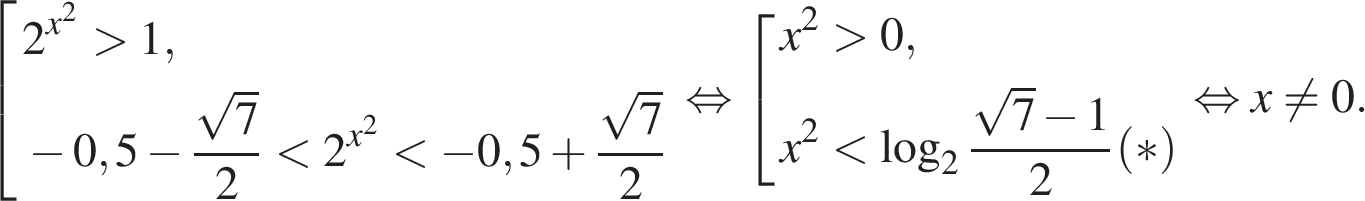
Вы получите 1 балл из 2, если:
-
Допущена единичная ошибка, возможно, приведшая к неверному ответу, но при этом имеется верная последовательность всех шагов решения
Приложение 2
-
группа
1)
3)
Ответы: 1)
2)
3)
-
группа
Решите неравенство с полным обоснованием решения:
1)
2)
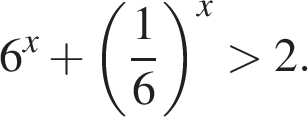
3)
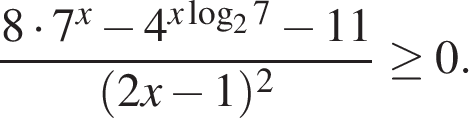
Ответы: 1)
2)
2 группа
Решите неравенство с полным обоснованием решения:
1)
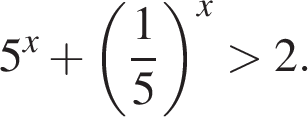
3)
Ответы: 1)
2)
3)
 Проверочная работа (в одном варианте)
Проверочная работа (в одном варианте)
Решите неравенства:
1)
2)
5)
6)
7)
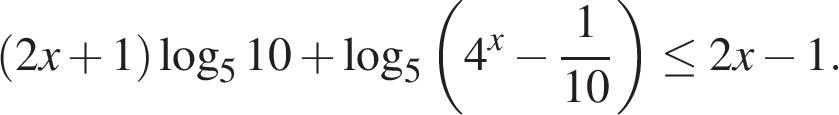
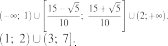 Ответы:
Ответы:1)
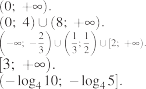 2)
2)3)
4)
5)
6)
7)
Задания С-3 ЕГЭ проверяют высокий уровень владения материалом. Кадеты должны показать знания теорем о равносильности неравенств определѐнного вида, умения использовать стандартные и нестандартные методы решения.
Целью данной работы является систематизация, обобщение основных приѐмов решения неравенств и систем неравенств повышенного уровня сложности.
При изучении данной темы кадеты (имеющие особые способности к изучению математики, так как базовый уровень знаний не является достаточным для усвоения данного материала) научились применять теоремы о равносильности неравенств определенного вида, познакомились со стандартными и нестандартными методами решения неравенств. Применили эти способы при