Файл: Численное моделирование ламинарного потока в канале.docx

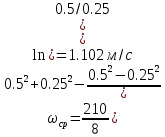
Re=200:





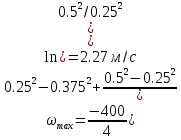
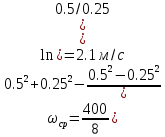
Re=400:





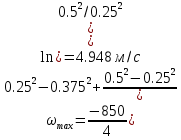
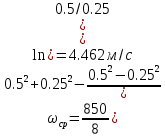
Таблица 3 – сравнение расчётных и аналитических значений скоростей потока для разных чисел Рейнольдса

Re	100	200	400
Vmax, м/с	1.501	2.997	5.893
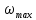, м/с	1.222	2.27	4.948
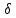, %	19	22	16

где Vmax – расчётная максимальная скорость, 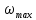— аналитически найденная максимальная скорость потока, 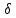– погрешность.

Таблица 4 – сравнение расчётных и аналитических значений средних скоростей потока для разных чисел Рейнольдса

Re	100	200	400
Vср, м/с	1	2	4
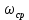, м/с	1.102	2.1	4.462
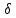, %	10	5	11

где Vср – расчётная максимальная скорость, 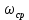— аналитически найденная максимальная скорость потока, 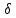– погрешность.
Данные решения можно назвать только приближенными в связи с тем, что некоторые величины рассчитаны не аналитическим способом. Полученные значения максимальной скорости получились достаточно точными, погрешность не превышает 11%.

---

Теоретические значения коэффициентов сопротивления 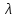определялись по формуле [2]: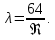



Тогда:

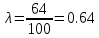— для Re=100.

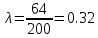— для Re=200.

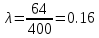— для Re=400.

Численное значение коэффициента сопротивления 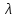определялось по формуле с использованием значений, полученных в Ansys CFD-Post: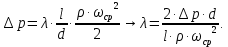



где 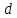— гидравлический диаметр трубы (d = d_внеш – d_внутр); — длина исследуемого участка с установившемся течением; — плотность; — средняя скорость потока, рассчитываемая по формуле:

Тогда расчётный коэффициент сопротивления для исследуемых чисел Рейнольдса:

Re=100:

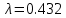
Re=200:

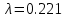
Re=400:

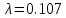
Таблица 4 – сравнение расчётных и аналитических значений коэффициентов сопротивления потока для разных чисел Рейнольдса

Re	100	200	400
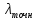	0.64	0.32	0.16
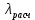	0.432	0.221	0.107
, %	32	30	33

---

где
– расчётный коэффициент сопротивления потока, — аналитически найденный коэффициент сопротивления потока, – погрешность.

Вывод

В данной работе был проведён численный расчет стационарного ламинарного течения вязкой несжимаемой жидкости в трубки кольцеобразного сечения для разных значений числа Рейнольдса: 100, 200, 400 с использованием расчётной программы Fluent.

Были построены геометрия, расчётная сетка, проанализированы поля скоростей в потоке, профили скорости и построены распределения давления и касательных напряжений на внутренней и внешней стенках трубы.

Были рассчитаны и вычислены аналитически средняя скорость (максимальная погрешность составила 11%), максимальная скорость (максимальная погрешность составила 22%), а также коэффициент сопротивления потока (максимальная погрешность составила 33%).

Список литературы

1. 
   Лойцянский Л. Г. (1950). Механика жидкости и газа. Ленинград: Гоосударственное издательство технико-теоретической литературы.
   

---