Добавлен: 03.12.2023
Просмотров: 325
Скачиваний: 6
СОДЕРЖАНИЕ
1. Классификация многогранников
1.1. Основные понятия и определения
1.2. Классификация многогранников по количеству граней
1.3. Классификация многогранников по регулярности
2.1. Определение правильных многогранников
2.2. Существование и единственность правильных многогранников
2.3. Построение правильных многогранников
2.4. Примеры правильных многогранников
3.1. Определение неправильных многогранников
3.2. Классификация неправильных многогранников
3.3. Построение неправильных многогранников
3.4. Примеры неправильных многогранников
4.1 Описание основных особенностей многогранников
4.3. Формула Эйлера для многогранников
4.4. Дуальность многогранников
5.1. Геометрические приложения многогранников
5.2. Использование многогранников в науке и технике
Тема: Многогранники
Титульный лист
Содержание
Введение 4
1. Классификация многогранников 6
1.1. Основные понятия и определения 6
1.2. Классификация многогранников по количеству граней 8
1.3. Классификация многогранников по регулярности 11
2. Правильные многогранники 12
2.1. Определение правильных многогранников 12
2.2. Существование и единственность правильных многогранников 12
2.3. Построение правильных многогранников 13
2.4. Примеры правильных многогранников 14
3. Неправильные многогранники 15
3.1. Определение неправильных многогранников 15
3.2. Классификация неправильных многогранников 15
3.3. Построение неправильных многогранников 17
3.4. Примеры неправильных многогранников 18
4. Особенности многогранников 20
4.1 Описание основных особенностей многогранников 20
4.2. Понятие рёберного графа 21
4.3. Формула Эйлера для многогранников 21
4.4. Дуальность многогранников 22
5. Применения многогранников 23
5.1. Геометрические приложения многогранников 23
5.2. Использование многогранников в науке и технике 24
5.3. Применение многогранников в искусстве 24
Заключение 26
Список используемых источников 27
Введение
Многогранник - это геометрическое тело, ограниченное плоскими многоугольниками, называемыми гранями. Каждая грань соединяется с другими гранями по рёбрам, которые являются линейными отрезками. Точки пересечения рёбер называются вершинами многогранника.
Многогранники могут быть трехмерными, четырехмерными и т.д. В трехмерном пространстве наиболее известными многогранниками являются куб, тетраэдр, октаэдр, додекаэдр, икосаэдр и т.д.
Многогранники имеют важное значение в геометрии и других науках, таких как математика, физика, химия и технические науки. Они широко используются в архитектуре, дизайне и искусстве как формы для создания объектов и композиций.
Изучение многогранников имеет длинную историю, которая начинается с античности. Одним из первых ученых, которые изучали многогранники, был греческий математик Евклид. В его знаменитой книге "Начала" были описаны основные свойства многогранников, включая правильные многогранники.
Следующий важный вклад в исследование многогранников был сделан в XVI веке немецким математиком Юргеном Штевио. Он разработал теорию многогранников и предложил свой метод их классификации.
В XIX веке Георг Клейн изучал многогранники как часть своей работы по теории групп. Он опубликовал множество работ, в которых рассматривал различные свойства многогранников и классификацию их симметрий.
С начала XX века многогранники стали активно изучаться в контексте топологии, геометрии и комбинаторики. Наиболее известные ученые, которые внесли вклад в исследование многогранников, это Джордж Биркхофф, Петер Мюнд и Бруно Бауэр.
В 1960-х годах многогранники получили новый импульс в исследованиях благодаря появлению компьютеров и возможности компьютерного моделирования. Это привело к развитию новых алгоритмов, которые позволили быстро и эффективно исследовать свойства многогранников в различных размерностях.
В настоящее время многогранники продолжают привлекать внимание ученых и находят широкое применение в различных областях науки и техники, таких как компьютерная графика, кристаллография, теория кодирования и другие.
1. Классификация многогранников
1.1. Основные понятия и определения
Для того чтобы лучше понимать многогранники, необходимо знать основные понятия и определения, связанные с этой темой. Рассмотрим некоторые из них:
1. Вершина. Вершина многогранника - это точка, где сходятся не менее трех ребер.
2. Ребро. Ребро многогранника - это отрезок, соединяющий две вершины.
3. Грань. Грань многогранника - это многогранник, образованный пересечением плоскости с многогранником. Грани могут быть треугольниками, четырехугольниками и т.д (Рисунок 1).
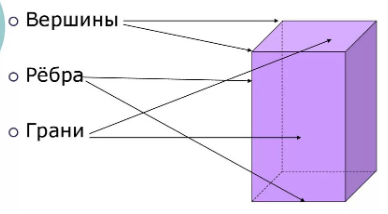
Рисунок 1 – Элементы многогранника
4. Размерность. Размерность многогранника - это число, указывающее на количество координат, необходимых для его описания. Например, для трехмерного многогранника необходимо три координаты.
5. Полиэдр. Полиэдр - это многогранник, все грани которого являются плоскими многоугольниками.
6. Правильный многогранник. Правильный многогранник - это многогранник, у которого все грани правильные многоугольники и все углы между гранями равны.
7. Дуальный многогранник. Дуальный многогранник - это многогранник, полученный из исходного многогранника путем замены вершин гранями и граней вершинами (Рисунок 2).
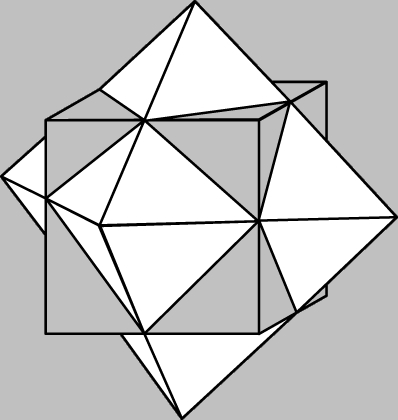
Рисунок 2 – Октаэдр двойственен кубу
8. Плоский граф. Плоский граф - это граф, который можно нарисовать на плоскости без пересечения ребер.
9. Графический полиэдр. Графический полиэдр - это полиэдр, построенный на основе плоского графа, где каждой вершине графа соответствует вершина многогранника, а каждому ребру - ребро многогранника.
Это лишь некоторые из основных понятий и определений, связанных с многогранниками. Знание этих понятий поможет лучше понять структуру многогранников и их свойства.
1.2. Классификация многогранников по количеству граней
Многогранники могут быть классифицированы по количеству граней, которые они имеют. Вот некоторые из наиболее распространенных классов многогранников по количеству граней:
1. Тетраэдр. Тетраэдр - это многогранник, у которого 4 грани. (Рисунок 3)

Рисунок 3 – Тетраэдр
2. Гексаэдр (куб). Гексаэдр, также известный как куб, - это многогранник, у которого 6 граней. (Рисунок 4)
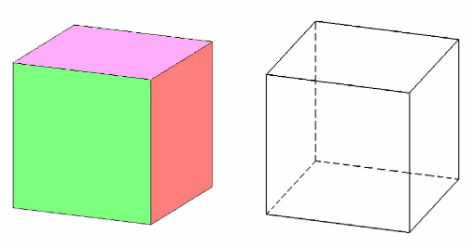
Рисунок 4 – Гексаэдр (куб)
3. Октаэдр. Октаэдр - это многогранник, у которого 8 граней. (Рисунок 5)
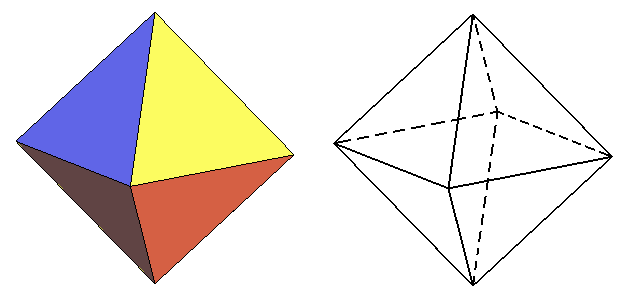
Рисунок 5 – Октаэдр
4. Додекаэдр. Додекаэдр - это многогранник, у которого 12 граней. (Рисунок 6)
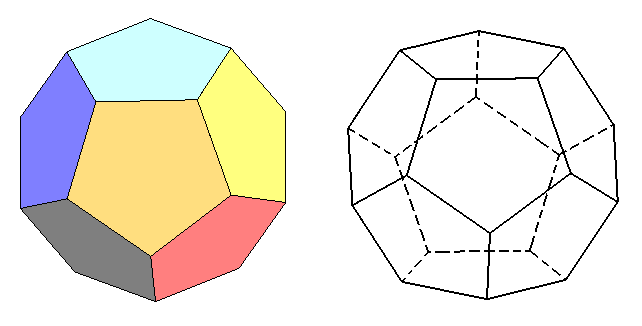
Рисунок 6 – Додекаэдр
5. Икосаэдр. Икосаэдр - это многогранник, у которого 20 граней. (Рисунок 7)
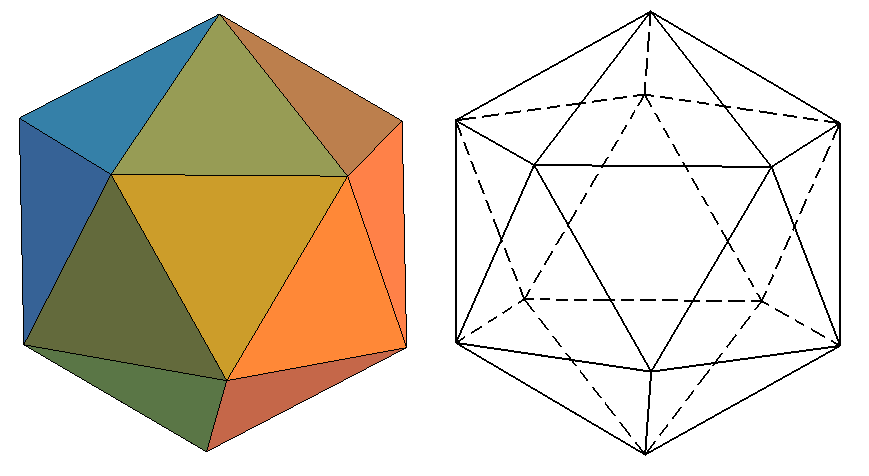
Рисунок 7 – Икосаэдр
6. Пирамида. Пирамида - это многогранник, у которого одна грань (основание) является многоугольником, а все остальные грани являются треугольниками.
7. Призма. Призма - это многогранник, у которого две параллельные грани (основания) являются многоугольниками, а все остальные грани являются прямоугольниками.
8. Антипризма. Антипризма - это многогранник, у которого две параллельные грани (основания) являются правильными многоугольниками, а все остальные грани являются равнобедренными треугольниками.
Антипризмы похожи на призмы, за исключением того, что основания скручены относительно друг друга, и что боковые грани (соединяющие основания) представляют собой 2n треугольников, а не n четырехугольников.
Это лишь некоторые из возможных многогранников, их разновидностей и типов, которые можно выделить в зависимости от количества граней. Классификация многогранников по количеству граней имеет большое значение в геометрии и математике, так как позволяет систематизировать знания и делает возможным более глубокое изучение свойств многогранников.
1.3. Классификация многогранников по регулярности
Многогранники могут быть классифицированы по степени их регулярности. Регулярные многогранники имеют все грани правильных многоугольников одинакового размера и формы, а также все углы между гранями равны между собой. Нерегулярные многогранники могут иметь различные размеры и формы граней, а также различные углы между гранями.
Регулярные многогранники можно классифицировать следующим образом:
1. Тетраэдр. Тетраэдр является регулярным многогранником, так как у него 4 правильные треугольные грани.
2. Гексаэдр (куб). Гексаэдр, также известный как куб, является регулярным многогранником, так как у него 6 квадратных граней.
3. Октаэдр. Октаэдр является регулярным многогранником, так как у него 8 правильных треугольных граней.
4. Додекаэдр. Додекаэдр является регулярным многогранником, так как у него 12 правильных пятиугольных граней.
5. Икосаэдр. Икосаэдр является регулярным многогранником, так как у него 20 правильных треугольных граней.
Кроме того, регулярные многогранники могут быть классифицированы по количеству вершин, которые они имеют. Для каждого числа вершин существует только определенное количество регулярных многогранников.
Таким образом, классификация многогранников по их регулярности является важной частью геометрии и математики, так как она помогает определить свойства и структуру многогранников.
2. Правильные многогранники
2.1. Определение правильных многогранников
Правильный многогранник - это многогранник, у которого все грани равны и правильны (то есть имеют одинаковую форму и размер), а также все углы между гранями равны между собой.
Например, правильный тетраэдр имеет 4 правильных треугольных грани, правильный гексаэдр (куб) имеет 6 квадратных граней, правильный октаэдр имеет 8 правильных треугольных граней, правильный додекаэдр имеет 12 правильных пятиугольных граней, а правильный икосаэдр имеет 20 правильных треугольных граней.
Правильные многогранники имеют множество интересных свойств и структурных особенностей, которые делают их важными в геометрии и других науках. Например, правильные многогранники могут быть использованы в кристаллографии для описания структуры кристаллов, в топологии для изучения поверхностей, и в математике для изучения симметрий и групп симметрии.
2.2. Существование и единственность правильных многогранников
Существование правильных многогранников зависит от количества граней, угла между гранями и размера многогранника. Есть только пять видов правильных многогранников в трехмерном пространстве: тетраэдр, куб (гексаэдр), октаэдр, додекаэдр и икосаэдр. Каждый из этих многогранников имеет одинаковые грани и равные углы между ними.
Единственность правильных многогранников также зависит от их количества граней и угла между ними. Существует только один правильный тетраэдр, один правильный куб, один правильный октаэдр, один правильный додекаэдр и один правильный икосаэдр. Это значит, что если многогранник имеет такое же количество граней и такой же угол между ними, как правильный многогранник, то он будет точно таким же, как правильный многогранник.
Существует формула Эйлера, которая связывает количество вершин, граней и ребер многогранника: V - E + F = 2, где V - количество вершин, E - количество ребер и F - количество граней. Эта формула позволяет вычислять количество граней, ребер и вершин правильных многогранников с заданным количеством граней.
Однако не все многогранники могут быть правильными. Например, существуют многогранники, у которых одна или несколько граней выпуклы, но не равны, и/или углы между гранями не равны между собой. Такие многогранники называются неправильными.
2.3. Построение правильных многогранников
Правильные многогранники могут быть построены различными способами, но самый распространенный способ - это использование геометрических преобразований, таких как повороты, симметрии и переносы, для получения правильной формы.
Например, куб может быть построен путем соединения 8 вершин равномерными отрезками и построения 6 граней, каждая из которых является квадратом. Другой способ построения куба - это использование правильного тетраэдра, вращение его вокруг оси, проходящей через центры двух противоположных граней, и соединение полученных вершин равномерными отрезками.
Октаэдр может быть построен путем соединения 6 вершин, каждая из которых является вершиной правильного треугольника, и построения 8 граней, каждая из которых является правильным треугольником. Другой способ построения октаэдра - это использование куба, соединение его диагоналей и усечение углов, чтобы получить правильные треугольники.
Икосаэдр и додекаэдр могут быть построены путем соединения вершин правильного пятиугольника и построения соответствующих граней. Эти многогранники могут быть построены также путем использования правильного треугольника и построения новых граней путем соединения его вершин.