Файл: Тема Многогранники Титульный лист Содержание.docx

Все эти построения требуют точности и внимательности, но с помощью них можно получить правильные многогранники.

2.4. Примеры правильных многогранников

Примеры правильных многогранников в трехмерном пространстве:

1. Тетраэдр - имеет 4 правильных треугольных грани и 4 равных равнобедренных треугольных грани.

2. Куб - имеет 6 квадратных граней, каждая из которых является правильной и имеет равную длину сторон.

3. Октаэдр - имеет 8 правильных треугольных граней.

4. Додекаэдр - имеет 12 правильных пятиугольных граней.

5. Икосаэдр - имеет 20 правильных треугольных граней.

Примеры правильных многогранников в более высоких размерностях:

1. Симплекс - это правильный треугольник в двумерном пространстве, правильный тетраэдр в трехмерном пространстве, и т.д.

2. Гиперкуб - это правильный куб в четырехмерном пространстве, а его аналоги в более высоких размерностях называются гиперкубами.

3. 120-гранник - это правильный многогранник в четырехмерном пространстве, имеющий 120 правильных пятиугольных граней.

4. 600-гранник - это правильный многогранник в четырехмерном пространстве, имеющий 600 правильных треугольных граней.

5. 120-мерный симплекс - это правильный симплекс в 120-мерном пространстве, имеющий 121 вершину и 7260 граней.

3. Неправильные многогранники

3.1. Определение неправильных многогранников

Неправильные многогранники - это многогранники, у которых не все грани равны и не все углы между гранями равны. Такие многогранники могут иметь различные формы и размеры граней, а также различные углы между гранями.

Например, если взять куб и рассмотреть его грани как равнобедренные трапеции, то получится неправильный многогранник, у которого грани не являются правильными квадратами, а углы между гранями не являются прямыми.

Неправильные многогранники могут быть более сложными и иметь различные комбинации граней и углов. Их структура и форма зависят от числа граней, их формы и взаимного расположения.

3.2. Классификация неправильных многогранников

Неправильные многогранники можно классифицировать по различным признакам, например:

1. По числу граней:

- Триакис-тетраэдр - имеет 12 граней, каждая из которых является равнобедренной трапецией. (Рисунок 8)



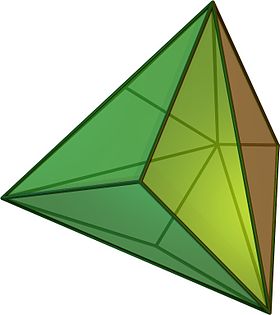
Рисунок 8 – Триакис-тетраэдр

---

- Пентакис-додекаэдр - имеет 60 граней, каждая из которых является равнобедренной трапецией.

2. По типу граней:

- Тетрагонально-додекаэдр - имеет 12 правильных пятиугольных граней и 4 правильных треугольных грани.

- Шестиугольно-додекаэдр - имеет 12 правильных пятиугольных граней и 6 правильных шестиугольных граней.

3. По степени симметрии:

- Комбинированный додекаэдр - имеет различные грани и не обладает никакой особым симметрией.

- Триаконтагексаэдр - обладает 32-кратной симметрией и имеет 62 грани, каждая из которых является равнобедренной трапецией.

4. По форме:

- Ромбический додекаэдр - имеет 12 ромбических граней и выглядит как утолщенный куб.

- Ромбоэдрический икосаэдр - имеет 20 ромбических граней и выглядит как утолщенный икосаэдр.

Это лишь некоторые примеры классификации неправильных многогранников, поскольку их разнообразие очень велико и они могут быть очень различными по своим характеристикам.

3.3. Построение неправильных многогранников

Построение неправильных многогранников - это процесс, при котором нарушаются условия правильности многогранника, например, углы между гранями могут быть различными, грани могут иметь разные размеры, формы и т.д.

Существует несколько методов построения неправильных многогранников, вот некоторые из них:

1. Метод "секущих плоскостей":

Этот метод заключается в том, чтобы применять секущие плоскости к правильному многограннику под определенным углом и затем отбрасывать все те части многогранника, которые находятся за плоскостями. Этот процесс может быть продолжен до тех пор, пока не будет получен неправильный многогранник.

2. Метод "сращивания граней":

В этом методе различные грани правильного многогранника сращиваются вместе, чтобы создать новые грани и изменить форму многогранника.

3. Метод "склеивания многогранников":

В этом методе несколько правильных многогранников склеиваются вместе, чтобы создать новый многогранник, который может быть неправильным.

4. Метод "модификации граней":

В этом методе грани правильного многогранника модифицируются, например, путем удаления части грани или добавления новых участков, чтобы создать новый многогранник.

Важно отметить, что некоторые неправильные многогранники могут быть получены путем комбинации нескольких методов, а некоторые могут быть созданы только при помощи сложных алгоритмов, например, при моделировании молекул.

3.4. Примеры неправильных многогранников

---

Вот несколько примеров неправильных многогранников:

1. Тетраэдр

Тетраэдр - это простейший многогранник, который состоит из четырех треугольных граней. Он является правильным многогранником, но если изменить размеры его граней, то можно получить неправильный тетраэдр.

2. Кубооктаэдр

Кубооктаэдр - это многогранник, который имеет 14 граней: 8 равносторонних треугольников и 6 квадратов. Он является неправильным многогранником, так как у него нет одинаковых граней.

3. Икосаэдр

Икосаэдр - это многогранник, который имеет 20 граней: 12 правильных пятиугольников и 8 правильных треугольников. Он является правильным многогранником, но если изменить форму его граней, то можно получить неправильный икосаэдр.

4. Кусочно-правильный тетраэдр

Кусочно-правильный тетраэдр - это многогранник, который состоит из четырех равносторонних треугольных граней, но при этом имеет разные длины ребер и разные углы между гранями. Он является неправильным многогранником.

5. Квартика

Квартика - это многогранник, который имеет 24 грани: 8 правильных треугольников и 16 равных выпуклых пятиугольников. Он является неправильным многогранником, так как у него нет одинаковых граней и не выполняются условия правильности.

4. Особенности многогранников

4.1 Описание основных особенностей многогранников

Многогранники - это геометрические фигуры, которые имеют три или более размерности и обладают следующими особенностями:

1. Грани: многогранники состоят из граней - плоских фигур, которые ограничивают многогранник.

2. Ребра: многогранники имеют ребра - отрезки, которые соединяют вершины многогранника и образуют его каркас.

3. Вершины: многогранники имеют вершины - точки, в которых сходятся ребра многогранника.

4. Размерность: многогранники могут быть трехмерными (как куб или икосаэдр), четырехмерными (как гиперкуб или тессеракт) или иметь более высокую размерность.

5. Правильность: многогранники могут быть правильными, если все их грани являются правильными полигонами и все углы и ребра равны, или неправильными, если хотя бы одна грань не является правильной или у них не все грани равны.

6. Количество граней: многогранники могут иметь разное количество граней, что приводит к различной сложности их построения и изучения.

7. Симметрия: многогранники могут иметь различную степень симметрии, которая определяется количеством и типом поворотов, которые сохраняют их форму.

---

8. Пространственная форма: многогранники могут иметь различные формы в пространстве, такие как сферические, конические, цилиндрические и т.д.

9. Приложения: многогранники находят применение в различных областях, таких как математика, физика, химия, компьютерная графика и дизайн.

4.2. Понятие рёберного графа

Рёберный граф (также называемый графом рёбер или линейным графом) многогранника является графом, вершины которого соответствуют ребрам многогранника, а ребра графа - граням многогранника.

В рёберном графе каждая вершина соединена ребром с теми гранями многогранника, которые содержат соответствующее ребро. Ребра графа образуют циклы, называемые циклами графа или циклами Эйлера.

Рёберный граф помогает исследовать структуру многогранника, его свойства и характеристики, такие как количество граней, вершин и ребер, а также симметрии и свойства его рёбер и граней.

Рёберный граф также находит применение в комбинаторике и теории графов, где может быть использован для решения различных задач, таких как поиск циклов и путей в графах, определение свойств графов и т.д.

4.3. Формула Эйлера для многогранников

Формула Эйлера для многогранников является одной из основных формул теории многогранников и связывает число вершин, рёбер и граней многогранника. Формула выглядит следующим образом:

V - E + F = 2,

где V - число вершин, E - число рёбер, F - число граней многогранника.

Формула Эйлера для многогранников доказывается с использованием рёберного графа многогранника. Для этого рассматривается сумма степеней вершин рёберного графа, которая равна удвоенному числу рёбер графа. С другой стороны, эта сумма равна также числу граней, умноженному на среднее число рёбер на грань (или, что равносильно, на число рёбер, инцидентных каждой грани). Затем, используя формулу Эйлера для плоских графов, получаем:

2E = Vd_1 + 2d_2 + ... + kd_k,

где d_i - степень вершины i, k - число вершин.

Из этого следует, что

2E = 2F + V - k.

Из этого равенства и формулы Эйлера для плоских графов (V - E + F = 2) получаем формулу Эйлера для многогранников:

V - E + F = 2.

4.4. Дуальность многогранников

Дуальность многогранников - это свойство многогранников, при котором каждой грани исходного многогранника соответствует вершина двойственного многогранника, и наоборот. То есть, если рассмотреть плоскую фигуру и построить ее двойственную фигуру, то каждой грани первой фигуры будет соответствовать вершина второй фигуры.

---

Более формально, двойственный многогранник получается следующим образом: каждой грани исходного многогранника ставится в соответствие вершина двойственного многогранника, а каждой вершине исходного многогранника - грань двойственного многогранника. Ребро двойственного многогранника проводится между вершинами, соответствующими граням, которые имеют общую вершину в исходном многограннике.

Дуальность многогранников является важным инструментом в теории многогранников и имеет множество приложений в различных областях математики и физики. Например, двойственность многогранников используется при построении топологических моделей молекул, при решении задач комбинаторной оптимизации, а также в кристаллографии для определения симметрии кристаллов.

Примером двойственности многогранников является пара правильных многогранников - октаэдр и куб. В октаэдре 6 вершин, 12 ребер и 8 граней, а в кубе - 8 вершин, 12 ребер и 6 граней. Двойственный многогранник к октаэдру будет куб, а к кубу - октаэдр. В кубе вершинами являются центры граней октаэдра, а в октаэдре - центры граней куба.

5. Применения многогранников

5.1. Геометрические приложения многогранников

Многогранники имеют множество геометрических приложений в различных областях. Некоторые из них включают:

1. Кристаллография: Многогранники используются для описания кристаллических структур и кристаллических решеток. Кристаллические структуры могут быть представлены в виде комбинации правильных и неправильных многогранников.

2. Архитектура: Правильные многогранники и их производные используются в архитектуре для создания необычных форм зданий и сооружений.

3. Графика: Многогранники используются в трехмерной графике и компьютерной графике для создания 3D-моделей объектов.

4. Геодезия: Многогранники используются в геодезии для измерения и описания формы Земли и других планет.

5. Физика: Многогранники используются в физике для описания кристаллических структур и симметрий в кристаллах, а также для описания элементарных частиц и их взаимодействия.

6. Химия: Многогранники используются в химии для описания структур молекул и кристаллических решеток.

7. Игры: Многогранники используются в играх, таких как кости и кубики, для создания интересных форм и структур.

8. Дизайн: Многогранники используются в дизайне для создания интересных и необычных форм и структур.

9. Математическое исследование: Многогранники являются объектом исследования в математике и теории графов, и многие из их свойств и связанных с ними теорем являются предметом математических исследований.

---