Файл: Методические указания к практическим занятиям по диисциплине основы теории надежности.docx

Министерство образования и науки Российской Федерации
Государственное бюджетное образовательное учреждение высшего профессионального образования

«Владимирский государственный университет имени Александра Григорьевича и Николя Григорьевича Столетовых»

Кафедра УКТР

методические указания к практическим занятиям по диисциплине «основы теории надежности»
модуль 1. «Количественные характеристики надежности. Расчет характеристик надежности невосстанавливаемых изделий при основном соединении элементов»


Специальность 220501 «Управление качеством», заочная форма обучения.


Составитель:

З.В. мищенко

Владимир 2012
1. КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
1.1. ТИПОВЫЕ ПРИМЕРЫ И ИХ РЕШЕНИЯ
Задачи, которые встречаются при определении количественных характеристик надежности, могут быть разбиты на следующие группы:

1) определение количественных характеристик на­дежности по статистическим данным об отказах изделия;

2) определение количественных характеристик на­дежности изделия при известном аналитическом выра­жении одной какой-либо характеристики.

При решении задач первой группы используются статистические определения количественных характеристик надежности, при решении задач второй группы - вероятностные определения характеристик и аналитические зависимости между ними.

В настоящей главе при определении количественных характеристик надежности технических устройств по статистическим данным об их отказах не учитывается до­стоверность полученных результатов. По этой причине иногда в примерах и задачах исходные данные о числе испытуемых образцов и количестве отказов приводятся без учета требований достоверности получения количест­венных характеристик надежности. Вопросы достоверно­сти результатов испытаний рассматриваются в пятой главе.

Следует иметь в виду, что частота, интенсивность от­казов и параметр потока отказов, вычисленные по фор­мулам (1.4), (1.6) и (1.13), являются постоянными в диапазоне интервала времени ∆t, а функции

---

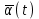
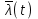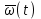, , - ступенчатыми кривыми или гистограммами.

Для удобства изложения в дальнейшем при решении задач на определение частоты, интенсивности и параметра потока отказов по статистическим данным об отказах изделий ответы относятся к середине интервала ∆t. При этом результаты вычислений графически представляются не в виде гистограмм, а в виде точек, отнесенных к середи­не интервалов ∆t_i и соединенных плавной кривой.

Рассмотрим типовые примеры.

Пример 1.1. На испытание поставлено N₀= 400 изделий. За время t = 3000 ч отказало n(t) = 200 изделий, за интервал времени ∆t =100 чотказало n(∆t) = 100 изделий (рис. 1.3). Требуется определить , , , .
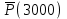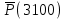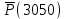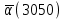
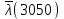t = 0t = 3000 ч ∆t = 1000 ч




N₀ = 400n(t) = 200n(∆t) = 100

N_i= 200N_i+1= 100
Рис. 1.3. Временной график к примеру 1.1.
Решение: 1. По формуле (1.2) найдем вероятность безотказной работы:

для t_Н = 3000 ч (начало интервала)

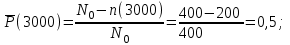
для t_К = 3100 ч (конец интервала)

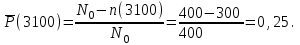
Определим среднее число исправно работающих образ­цов в интервале ∆t

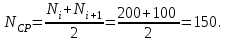
Число отказавших изделий за время t= 3050 ч


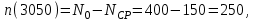
тогда

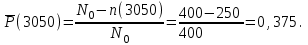
2. По формуле (1.4) определяем частоту отказа:

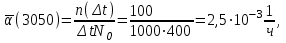
3. По формуле (1.6) определяем частоту отказа:

---

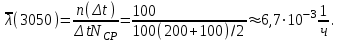
Интенсивность отказа можно также определить по формуле (1.7):


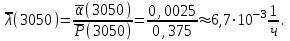
Пример 1.2. Производилось наблюдение за работой трех экземпляров однотипной аппаратуры. За период на­блюдения было зафиксировано по первому экземпляру аппаратуры 6 отказов, по второму и третьему - 11 и 8 отказов соответственно. Наработка первого экземпляра составила 181 час, второго - 329 и третьего - 245 ч. Требуется определить наработку аппаратуры на отказ.
Решение. 1. Определяем суммарную наработку трех образцов аппаратуры:
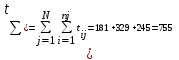ч.

2. 
   Определяем суммарное количество отказов:
   

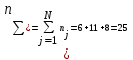отказов.
3. Находим среднюю наработку на отказ по формуле (1.19):
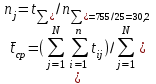ч.
Пример 1.3. Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый прибор отказал 34 раза в течение 952 ч работы, второй - 24 раза в течение 960 ч работы, а остальные приборы в течение 210 ч работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов.

Решение. Для решения данной задачи воспользуем­ся следующими соотношениям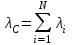и:
и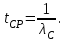
1. Определим интенсивность отказов для каждого прибора:


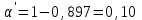
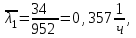
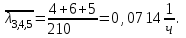
2. Интенсивность отказов системы будет

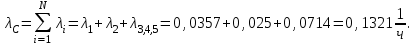
3. Средняя наработка на отказ системы равна
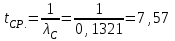ч.

Пример 1.4. Пусть время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром λ = 2,5- 10^-5 1/ч.

Требуется вычислить количественные характеристики надежности элемента P(t), a(t), Т_ср ,если t= 500, 1000, 2000 ч.

Решение. Используем формулы для P(t), a(t) и Т_ср, приведенные в табл. 1.1.

---

1. 
   Вычислим вероятность безотказной работы:
   

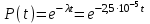
Используя данные табл. П. 7.14 [9], получим:

2. 
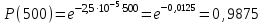
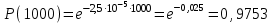
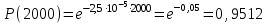
   Вычислим частоту отказа:
   

,




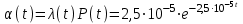
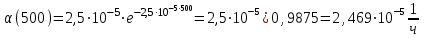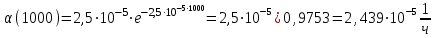
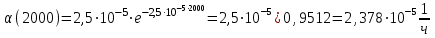
3. Вычислим среднюю наработку до первого отказа:
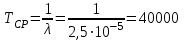ч.

1.2. Задачи
1.1. Допустим, что на испытание поставлено 1000 однотипных изделий. За первые 3000 ч отказало 80 изделий. За интервал времени 3000 - 4000 ч отказало еще 50. Требуется определить частоту и интенсивность отказов изделий в промежутке времени 3000 – 4000 ч.



1.2. В течение 1000 ч из 10 гироскопов отказало 2. За интервал времени 1000 – 1100 ч отказал еще один гироскоп. Требуется найти частоту и интенсивность отказов гироскопов в промежутке времени 1000 – 1100 ч.



1.3. На испытание поставлено 400 резисторов. За время наработки 10000 ч отказало 4 резистора. За последующие 1000 ч отказал еще 1 резистор. Определить частоту и интенсивность отказов резисторов в промежутке времени 10000 – 11000 ч.





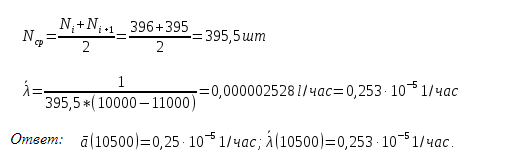
1.4. На испытание поставлено N₀=1000 изделий. За время t=0 ч вышло из строя n(t)=0 штук изделий. За последующий интервал времени t =1000 ч вышло из строя n(t)=20 изделий. Необходимо вычислить вероятность безотказной работы за время t и t+t, частоту отказов и интенсивность отказов на интервале t.

1.5. Интенсивность отказов изделия 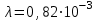1/ч = const. Необходимо найти вероятность безотказной работы системы в течение 6 ч

---

Р(6), частоту отказов а(100) при t=100 ч и среднюю наработку до первого отказа Т_ср.

Вероятность безотказной работы определим по формуле (1.8) [1]:
Р(t) = e - λt, тогда: Р(6) = exp(- 0,82·10-3·6) = e- 0,005 = 0,995.
А вероятность Р(100) = exp(- 0,82·10-3·100) = e- 0,082 = 0,921.
Из формулы (1.7) [1], находим частоту отказов а(t): а(t) = λ(t)·P(t), тогда:
а(100) = λ·Р(100) = 0,82·10-3·0,921 = 0,755·10-3 ,1/час.
При λ = const, из формулы (1.10) [1], можно получить формулу:
ТСР = 1/λ = 1/0,82·10-3 = 1219,5 ≈ 1220 час.
Ответ: Р(6) = 0,995; а(100) = 0,755·10-3, 1/час; ТСР = 1220 час.
1.6. Средняя наработка до первого отказа автоматической системы управления равна 640 ч. Предполагается, что справедлив экспоненциальный закон надежности. Необходимо определить вероятность безотказной работы в течение 120 ч, частоту отказов для момента времени 120 ч и интенсивность отказов.

В случае экспоненциального закона распределения для вычисления заданных количественных характеристик надежности системы применяются следующие формулы.
Вероятность безотказной работы P(t):
P(t) = e-λct, (1)
где λс – интенсивность отказов системы, 1/ч
Частота отказов f (t) системы:
f(t) =λс ·Р(t)=λс ·e-λct , (2)
При известном значении средней наработки до первого отказа Т0 интенсивность отказов системы λс можно определить по формуле:
λс =1Tc , (3)
λс =1Tc=1640 =0,00156 1/ч
Для t =120 ч
P(120) = e-λct=e-0,00156·120=0,829
f(120) =λс ·Р(t)=0,00156 ·0,829=0,00129 1/ч
Ответ: P(120) = 0,829; f(120) =0,00129 =1,29·10-3 1/ч;
λс =0,00156 =1,56·10-31/ч;
1.7. Средняя наработка изделия до первого отказа равна 1260 ч. Время исправной работы подчинено закону Релея. Необходимо найти его количественные характеристики надежности для t=1000 ч.

При распределении времени возникновения отказов по закону Релея основные показатели надежности определяются по следующим формулам.
Вероятность безотказной работы
P(t) = exp(-t2/2σt2), (1)
где σt – параметр закона распределения, ч
Вероятность отказа
Q(t) =1-P(t) =1- exp(-t2/2σt2), (2)
Частота отказов
f(t) =λ(t)∙P(t)=(t/σt2)exp(-t2/2σt2) , (3)
Интенсивность отказов
λ(t)=t/σt2, (4)
Cредняя наработка до первого отказа
mt = σtπ/2, (5)
Из формулы (4) при известном значении средней наработки изделия до первого отказа mt=1260 ч определим значение параметра σt:
σt=mtπ/2 =12603,14/2 =1006 ч
Подставив σt =1008 ч и t =1000 ч в формулы (1) ,(2) и (3), получим:
P(1000) = exp(-10002/2∙10062) = e-0,494= 0,61
Q(1000) =1-0,61=0,39
λ(1000)=1000/10062 =0,99∙10-3 1/ч
f(1000) = 0,99∙10-3·0,61= 0,6∙10-3 1/ч
Ответ: P(1000) =0,61 ; Q(1000) =0,39 ; f(1000) =0,6∙10-11/ ч ; mt=1260 ч
1.8. Вероятность безотказной работы гироскопа в течение t=150 ч равна 0,9. Время исправной работы подчинено закону Вейбулла с параметром k=2,6. Необходимо определить опасность отказов гироскопов для

---