Файл: Методические указания к практическим занятиям по диисциплине основы теории надежности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 683
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
t=150 ч. И среднюю наработку до первого отказа.
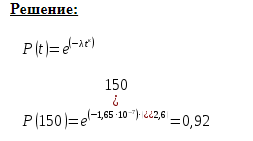
1.9. Частота отказов изделия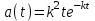 . Требуется определить параметр потока отказов (t).
. Требуется определить параметр потока отказов (t).
1. 10. При проведении форсированных испытаний изделия получена зависимость (t), приведенная на рис. 1.4. Необходимо найти вероятность безотказной работы в течение t=1000 ч, частоту отказов для t=1000 ч и среднюю наработку до первого отказа изделий.
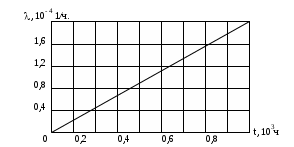
Рис. 1.4. Зависимость от t (к задаче 1.10)
1.11. Интенсивность отказов с сложной восстанавливаемой системы есть величина постоянная и равная 0,015 1/ч. Среднее время восстановления tв=100 ч. Необходимо вычислить вероятность застать систему в исправном состоянии в момент времени t=10 ч.
1.12. Коэффициент готовности сложного восстанавливаемого изделий Кг=0,9. Среднее время его восстановления tв=100 ч. Требуется найти вероятность застать изделие в исправном состоянии в момент времени t=12 ч.
1.13. Время работы изделия подчинено усеченному нормальному закону с параметрами Т1=8000 ч, 1=1000 ч. Требуется найти вероятность безотказно работы изделия в течение 8000 ч.
2. РАСЧЕТ ХАРАКТЕРИСТИК НАДЕЖНОСТИ
НЕВОССТАНАВЛИВАЕМЫХ ИЗДЕЛИЙ ПРИ ОСНОВНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ
2.1. ТИПОВЫЕ ПРИМЕРЫ
Пример 2.1. Система состоит из 12600 элементов, средняя интенсивность отказов которых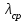 = 0,32.10-8 1/ч. Необходимо определить вероятность безотказной работы в течение t = 50 ч.
= 0,32.10-8 1/ч. Необходимо определить вероятность безотказной работы в течение t = 50 ч.
Решение. Интенсивность отказов системы по формуле (2.3) будет
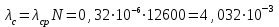 1/ч. Тогда на основании (2.2)
1/ч. Тогда на основании (2.2)
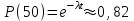
Пример 2.2. Система состоит из трех блоков, средняя наработка до первого отказа которых равна T1= 160 ч,T2= 320 ч,T3 = 600 ч. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднюю наработку до первого отказа системы.
Решение. Воспользуемся формулой (2.2) для средней наработки до первого отказа системы. В нашем случае
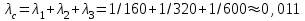 1/ч.
1/ч.
Тогда
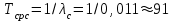 ч.
ч.
Пример 2.3. Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t=100 чравны: p1(100) =0,95; p2(100) = 0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы.
Решение. Найдем вероятность безотказной работы изделия: Pс(100) =p1(100).p2(100) =0,95-0,97 = 0,92.
Найдем интенсивность отказов изделия, воспользовавшись формулой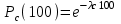 .
.
По таблице П. 7.14 [9] имеем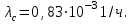 .
.
Тогда Тср с=1200 ч.
Пример 2.4. В системах могут быть использованы только элементы, интенсивность отказов которых равна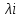 =10-5 1/ч.Системы имеют число элементов N1 = 500 и N2 = 2500. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа Рс(1).
=10-5 1/ч.Системы имеют число элементов N1 = 500 и N2 = 2500. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа Рс(1).
Решение. Интенсивность отказов систем соответственно будет
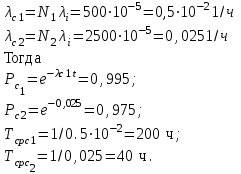
Тогда, задачу можно легко решить, используя номограмму приложения П. 1. 1 [9].
Пример 2.5. Система состоит из пяти приборов, вероятности исправной работы которых в течение времени t = 100 чравны: р1(100) =0,9996; р2(100) = 0,9998; p3 (100) = 0,9996; р4(100) =0,999; p5(100) =0,9998. Требуется определить частоту отказов системы в момент времени t= 100 ч.
Предполагается, что отказы приборов независимы •и для них справедлив экспоненциальный закон надежности.
Решение. По условию задачи отказы приборов независимы, поэтому вероятность безотказной работы системы равна произведению вероятностей безотказной работы приборов. Тогда по формуле (2.5) для случая высоконадежных систем имеем: P(100)=0,9978,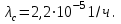
Тогда частота отказов в соответствии с формулой (2.4) будет
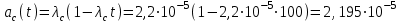 1/ч.
1/ч.
2.2. Задачи
2.1. Аппаратура связи состоит из 2000 элементов, средняя интенсивность отказов которых
ср=0,3310-5 1/ч. Необходимо определить вероятность безотказной работы аппаратуры в течение t= 200 ч и среднюю наработку до первого отказа.
2.2. Невосстанавливаемая в процессе радиоаппаратура сантиметрового диапазона состоит из 1000 элементов.
Требующиеся время непрерывной работы t= 200 ч. Определить вероятность безотказной работы и среднюю наработку до первого отказа, если l=0,110-5 1/ч.
2.3. Система состоит из N=20 приборов. Надежность приборов характеризуется вероятностью безотказной работы в течение времени t, которая равна: p1(t)=0,98; p2(t)=0,94; p3(t)=0,99; p4, 5, 6(t)=0,997; p7, 8, 9(t)=0,965; p10(t)=0,95; p11(t)=0,997; p12(t)=0,975; p13(t)=0,985; p14(t)=0,97; p15, 16, 17(t)=0,96; p18, 19(t)=0,995; p20(t)=0,945. Необходимо определить вероятность безотказной работы системы.
2.4. Система состоит из пяти приборов, средняя наработка до первого отказа которых равна: Т1=83 ч; Т2=220 ч; Т3=280 ч; Т4=400 ч; Т5=700 ч. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку доя первого отказа системы.
2.5. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени p1(50)=0,98; p2(50)=0,99; p3(50)=0,998; p4(50)=0,975; p5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку до первого отказа прибора.
2.6. Комплекс состоит из N=3 систем. Надежность отдельных систем характеризуется вероятностью безотказной работы в течение времени t, которая равна p1(t)=0,78, p2(t)=0,93, p3(t)=0,82. Определить вероятность безотказной работы комплекса.
2.7. Система состоит из двух блоков, средняя наработка до первого отказа которых равна Т1=200 ч; Т2=40 ч. Для блоков справедлив экспоненциальный закон надежности. Необходимо определить среднюю наработку системы до первого отказа.
2.8. Система состоит из трех устройств. Вероятность безотказной работы каждого из них в течение времени t= 100ч равна: p1(100)=0,95; p2(100)=0,96; p3(100)=0,97. Справедлив экспоненциальный закон надежности. Необходимо вычислить среднюю наработку до первого отказа системы.
Библиографический список
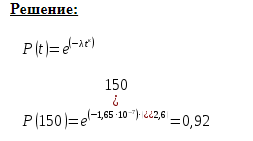
1.9. Частота отказов изделия
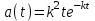 . Требуется определить параметр потока отказов (t).
. Требуется определить параметр потока отказов (t).1. 10. При проведении форсированных испытаний изделия получена зависимость (t), приведенная на рис. 1.4. Необходимо найти вероятность безотказной работы в течение t=1000 ч, частоту отказов для t=1000 ч и среднюю наработку до первого отказа изделий.

Рис. 1.4. Зависимость от t (к задаче 1.10)
1.11. Интенсивность отказов с сложной восстанавливаемой системы есть величина постоянная и равная 0,015 1/ч. Среднее время восстановления tв=100 ч. Необходимо вычислить вероятность застать систему в исправном состоянии в момент времени t=10 ч.
1.12. Коэффициент готовности сложного восстанавливаемого изделий Кг=0,9. Среднее время его восстановления tв=100 ч. Требуется найти вероятность застать изделие в исправном состоянии в момент времени t=12 ч.
1.13. Время работы изделия подчинено усеченному нормальному закону с параметрами Т1=8000 ч, 1=1000 ч. Требуется найти вероятность безотказно работы изделия в течение 8000 ч.
2. РАСЧЕТ ХАРАКТЕРИСТИК НАДЕЖНОСТИ
НЕВОССТАНАВЛИВАЕМЫХ ИЗДЕЛИЙ ПРИ ОСНОВНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ
2.1. ТИПОВЫЕ ПРИМЕРЫ
Пример 2.1. Система состоит из 12600 элементов, средняя интенсивность отказов которых
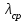 = 0,32.10-8 1/ч. Необходимо определить вероятность безотказной работы в течение t = 50 ч.
= 0,32.10-8 1/ч. Необходимо определить вероятность безотказной работы в течение t = 50 ч.Решение. Интенсивность отказов системы по формуле (2.3) будет
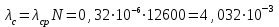 1/ч. Тогда на основании (2.2)
1/ч. Тогда на основании (2.2)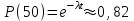
Пример 2.2. Система состоит из трех блоков, средняя наработка до первого отказа которых равна T1= 160 ч,T2= 320 ч,T3 = 600 ч. Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднюю наработку до первого отказа системы.
Решение. Воспользуемся формулой (2.2) для средней наработки до первого отказа системы. В нашем случае
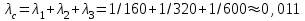 1/ч.
1/ч.Тогда
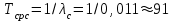 ч.
ч.Пример 2.3. Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t=100 чравны: p1(100) =0,95; p2(100) = 0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы.
Решение. Найдем вероятность безотказной работы изделия: Pс(100) =p1(100).p2(100) =0,95-0,97 = 0,92.
Найдем интенсивность отказов изделия, воспользовавшись формулой
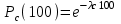 .
.По таблице П. 7.14 [9] имеем
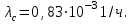 .
.Тогда Тср с=1200 ч.
Пример 2.4. В системах могут быть использованы только элементы, интенсивность отказов которых равна
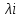 =10-5 1/ч.Системы имеют число элементов N1 = 500 и N2 = 2500. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа Рс(1).
=10-5 1/ч.Системы имеют число элементов N1 = 500 и N2 = 2500. Требуется определить среднюю наработку до первого отказа и вероятность безотказной работы в конце первого часа Рс(1).Решение. Интенсивность отказов систем соответственно будет
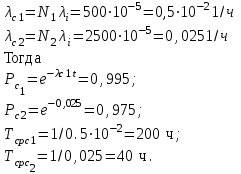
Тогда, задачу можно легко решить, используя номограмму приложения П. 1. 1 [9].
Пример 2.5. Система состоит из пяти приборов, вероятности исправной работы которых в течение времени t = 100 чравны: р1(100) =0,9996; р2(100) = 0,9998; p3 (100) = 0,9996; р4(100) =0,999; p5(100) =0,9998. Требуется определить частоту отказов системы в момент времени t= 100 ч.
Предполагается, что отказы приборов независимы •и для них справедлив экспоненциальный закон надежности.
Решение. По условию задачи отказы приборов независимы, поэтому вероятность безотказной работы системы равна произведению вероятностей безотказной работы приборов. Тогда по формуле (2.5) для случая высоконадежных систем имеем: P(100)=0,9978,
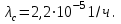
Тогда частота отказов в соответствии с формулой (2.4) будет
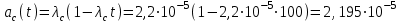 1/ч.
1/ч.2.2. Задачи
2.1. Аппаратура связи состоит из 2000 элементов, средняя интенсивность отказов которых
ср=0,3310-5 1/ч. Необходимо определить вероятность безотказной работы аппаратуры в течение t= 200 ч и среднюю наработку до первого отказа.
2.2. Невосстанавливаемая в процессе радиоаппаратура сантиметрового диапазона состоит из 1000 элементов.
Требующиеся время непрерывной работы t= 200 ч. Определить вероятность безотказной работы и среднюю наработку до первого отказа, если l=0,110-5 1/ч.
2.3. Система состоит из N=20 приборов. Надежность приборов характеризуется вероятностью безотказной работы в течение времени t, которая равна: p1(t)=0,98; p2(t)=0,94; p3(t)=0,99; p4, 5, 6(t)=0,997; p7, 8, 9(t)=0,965; p10(t)=0,95; p11(t)=0,997; p12(t)=0,975; p13(t)=0,985; p14(t)=0,97; p15, 16, 17(t)=0,96; p18, 19(t)=0,995; p20(t)=0,945. Необходимо определить вероятность безотказной работы системы.
2.4. Система состоит из пяти приборов, средняя наработка до первого отказа которых равна: Т1=83 ч; Т2=220 ч; Т3=280 ч; Т4=400 ч; Т5=700 ч. Для приборов справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку доя первого отказа системы.
2.5. Прибор состоит из пяти блоков. Вероятность безотказной работы каждого блока в течение времени p1(50)=0,98; p2(50)=0,99; p3(50)=0,998; p4(50)=0,975; p5(50)=0,985. Справедлив экспоненциальный закон надежности. Требуется найти среднюю наработку до первого отказа прибора.
2.6. Комплекс состоит из N=3 систем. Надежность отдельных систем характеризуется вероятностью безотказной работы в течение времени t, которая равна p1(t)=0,78, p2(t)=0,93, p3(t)=0,82. Определить вероятность безотказной работы комплекса.
2.7. Система состоит из двух блоков, средняя наработка до первого отказа которых равна Т1=200 ч; Т2=40 ч. Для блоков справедлив экспоненциальный закон надежности. Необходимо определить среднюю наработку системы до первого отказа.
2.8. Система состоит из трех устройств. Вероятность безотказной работы каждого из них в течение времени t= 100ч равна: p1(100)=0,95; p2(100)=0,96; p3(100)=0,97. Справедлив экспоненциальный закон надежности. Необходимо вычислить среднюю наработку до первого отказа системы.
Библиографический список
-
Острейковский В.А. Теория надежности: Учебник для ВУЗов. – М.: Высшая школа, 2003 г. – 345 с. -
Ястребенецкий М.А., Иванова Г.М. Надежность АСУТП: Учебное пособие для ВУЗов. – М.: Энергоатомиздат, 1989 г.- 264 с. -
Шураков В.В.Надежность программного обеспечения систем обработки данных: Учебник для ВУЗов. – М.: Энергоатомиздат, 1986 г. –272 с. -
Дружинин Г.В. Надежность автоматизированных производственных систем. – М.: Энергоатомиздат, 1986 г. – 480 с. -
Надежность и диагностирование технологического оборудования. М.: Наука, 1987 г. -
А.И. Кубарев. Надежность в машиностроении. Изд-во стандартов, 1989, 224 с. -
Б.Дилон, Ч. Сингх. Инженерные методы обеспечения надежности систем. Москва, Мир, 1984. -
Сборник задач по теории надежности. Под ред. А.М. Половко и И.М. Маликова. М., Изд-во «Советское радио», 1972, 408 стр. -
Шор Я.Б., Кузьмин Ф.Н. Таблицы для анализа и контроля надежности. Изд-во «Советское радио», 1968.
Оглавление
| Предисловие………………………………………………………………. | |
| 1. Количественные характеристики надежности……………………….. | |
| | |
| 1.1. Типовые примеры и их решения……………………………………. | |
| 1.2. Задачи………………………………………………………………… | |
| 2. Расчет характеристик надежности невосстанавливаемых изделий при основном соединении элементов…………………………………… | |
| | |
| 2.1. Типовые примеры и их решения……………………………………. | |
| 2.2. Задачи…………………………………………………………………. | |
| | |
| Библиографический список……………………………………………… | |