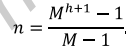Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 164

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВОПРОСЫ и ответы К ЭКЗАМЕНУ Комбинаторный признак умножения. Количество битовых строк длины k. Пусть задана последовательность событий E1, E2, E3, …, Em таких, что событие Е1осуществляется n1способами, и если события E1, E2, E3,...,Ек-1осуществились, то событие Ек может осуществиться nкспособами. Тогда существует n1х n2х n3х … х nтспособов осуществления всей последовательности событий.. Битовая строка – это строка, состоящая из элементов множества{0, 1}, т.е. каждый из элементов имеет значение 0 или 1. Сколько существует битовых строк длины 5? Сколько существует битовых строк длины k?Поскольку каждый символ строки может иметь значение 1 или 0, тосуществует два варианта выбора для каждой позиции. Следовательно, существует 2 x 2 x 2 x 2 x 2 = 25 битовых строк длины 5. По аналогичным соображениям, имеется 2k битовых строк длины k. Количество всех подмножеств k - элементного множества. Число всех подмножеств из элементов равно N(M(A))=2^n Комбинаторный признак сложения.  (Комбинаторный принцип сложения) Пусть S1, S 2, S3,... ,Sm – попарно непересекающиеся множества (т.е. SiSj = для всех i  j), и пусть для каждого i, множество Si содержит niэлементов. Количество вариантов вы­бора из S1 или S2или S3 или ... или Smравно n1 + n2 + n3+ … + nm. На языке теории множеств утверждение теоремы имеет вид |S1 S2 S3 ... Sm|= |S1| + |S2| + |S3| + ... + |Sm|, где |S| обозначает количество элементов множества S. Перестановки, размещения, сочетания без повторения. Перестановками -называются наборы состоящие из одного и того элементов,следования элементов. Pn=n!Размещение –называются упорядоченные наборы из элементов выбранных из n элементов, которые отличаются друг от друга, как порядком следования, так и составом элементов. mA =n!/(n-m)!nСочетание- называютсяэлементов выбранных из n элементов, которые отличаются другот друга составом элементов. mС =n!/m!(n-m)!n Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов. Формула бинома Ньютонадля натуральныхnимеет вид  , где   -биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).К примеру, известная формула сокращенного умножения "квадрат суммы" вида   есть частный случай бинома Ньютона приn=2.Выражение, которое находится в правой части формулы бинома Ньютона, называютразложениемвыражения(a+b)n, а выражение   называют(k+1)-ым членом разложения,k=0,1,2,…,n.Биномиальные коэффициенты для различныхnудобно представлять в виде таблицы, которая называется арифметическийтреугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид: Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральныхn: Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.Для коэффициентов бинома Ньютона справедливы следующие свойства: коэффициенты, равноудаленные от начала и конца разложения, равны между собой  ,p=0,1,2,…,n; ; сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона:  ; сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. Первые два свойства являются свойствами числа сочетаний. Перестановки, размещения, сочетания с повторениями. Перестановка – _ Размещение- Сочетание- 7. Признак клеток (Дирихле). Принцип Дирихле — простой, интуитивно понятный и часто полезный метод для доказательства утверждений о конечном множестве. Этот принцип часто используется в дискретной математике, где устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках данное утверждение известно как «принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики.Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, гдеn > mто, по крайней мере, в одной части будет более одного элемента.На языке отображений эта формулировка означает, чтоесли в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.Другая формулировка “ принципа Дирихле“:если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы двапредмета.В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “. [2] Признак математической индукции. Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному. Определение 2 9. Высказывания. Отрицание, конъюнкция, дизъюнкция, их таблицы истинности.Высказываниемназывается повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.Отрицаниемвысказывания  называется высказывание («не », «неверно, что »), которое истинно, когда ложно, и ложно, когда истинно.Таблица истинности для отрицания: Конъюнкцией (логическим умножением) двух высказываний  , называется высказывание (« и »), которое истинно только в том случае, когда и оба истинны.Таблица истинности для конъюнкций: Дизъюнкцией (логическим сложением) двух высказываний  , называется высказывание (« или »), которое истинно, когда хотя бы одно из них истинно.Таблица истинности для дизъюнкций: 10. Импликация и эквиваленция, таблицы их истинности.Импликацией двух высказываний  ,  называется высказывание  («если , то », « влечёт », «из следует », « имплицирует »), которое ложно тогда и только тогда, когда истинно, а ложно.Таблица истинности для импликаций:  Эквивалентностью высказываний  , называется высказывание (« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда  и  оба истинны или ложны.Таблица истинности для эквивалентности: 11. Эквивалентные высказывания. Теорема о свойствах логических эквивалентностей.Эквиваленцией (или эквивалентностью) двух высказываний Х, У называется новое высказывание, которое считается истинным, когда оба высказывания Х, У, либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.Эквиваленция высказываний Х, У обозначается символом  (или,

22. Булева алгебра.Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.23. Основные законы и свойства операций Булевой алгебры.Как любая алгебраическая система булева алгебра базируется на совокупности некоторых предположений, которые принято называть аксиомами, т.е предположениями не требующими доказательств. Аксиомы определяются для двух логических значений 1 ( "ИСТИНА" ) и 0 ( "ЛОЖЬ" ) и операций логического умножения (конъюнкции), которая обозначается " & ", " · " или не обозначается вовсе, логического сложения (дизъюнкции), которая обозначатся " v ", "+", и отрицания ( инверсии ), которая обозначается горизонтальной чертой (" - ") над переменной или выражением, например, . Булевой переменной, обозначаемой обычно xi , называется переменная принимающая два логических значения { 0, 1 }.Ниже приведены аксиомы булевой алгебры относительно дизъюнкции, конъюнкции и отрицания.Аксиомы конъюнкции 0·* 0 = 0 ; 1·* 1 = 1 ; 0·* 1 = 1·* 0 = 0 ;Аксиомы дизъюнкции 0 v 0 = 0 ; 1 v 1 = 1 ; 0 v 1 = 1 v 0 = 1 ;Аксиомы отрицания Если x = 0 , то ˆх = 1 ;Если x = 1 , то ˆх = 0 ;Следующие 5 правил обычно называют теоремами булевой алгебры. Особенностью теорем булевой алгебры является то, что для их доказательства пользуются простой подстановкой значений булевых переменных. Это обусловлено тем, что переменные могут принимать только 2 значения - 0 и 1.Операции с константами : Идемпотентность (тавтология, повторение) :  Для n переменных:  Противоречие :Правило "исключенного третьего" :Двойное отрицание (инволюция) :Следующие 4 правила обычно называют законами или тождествами булевой алгебры.Ассоциативность ( ассоциативный закон ) :   Коммутативность ( коммутативный закон ) :   11. Дистрибутивность ( дистрибутивный закон ) :конъюнкции относительно дизъюнкции: дизъюнкции относительно конъюнкции: 24. Отношения множеств. Область определения и множество значений отношения. Обратное отношение. Область определения отношения R – это подмножество всех элементов х множества Х, для которыхнайдется элемент y, связанный с данным элементом отношением R. Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R (). Пример: Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X. Итак, если R — отношение на множестве X, то R X X. Множество всех первых элементов пар из R называется областью определения отношения R. Множеством значений отношения R называется множество всех вторых элементов пар из R. Обратное отношение (отношение, обратное к R) — это двухместное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R. Обозначается: R−1. Для данного отношения и обратного ему верно равенство: (R−1)−1= R. Взаимо-обратные отношения(взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого. 25. Специальные свойства отношений на А. Частично упорядоченные множества.Бинарным отношением на множестве А называется подмножество его квадрата RÍ A2. Бинарным отношением между множествами А и В называются подмножество принадлежащее декартовому произведению 2-х множеств: RÍ АхВ.Если упорядоченная пара (а1, а2) принадлежит отношению R, то говорят что а1 R а2, то есть между элементом а1 и а2 уст-но отношение R.Областью определения бинарного отношения называется множество элементов а, в котором в принадлежит бинарному отношению: þR={a|bÎ aRb}.Областью значения бинарного отношения называют множество b, в котором а принадлежит бинарному значению:PR={b|aÎ aRb }.Обратное отношение для отношения R называется отношение: R-1={(b,a)|(a,b) Î R }.Отношение можно задать:-с помощью любого способа задания множеств-С помощью матрицы бинарного отношения. Матрица бинарного отношения это квадратная матрица R элементы которой определяются следующим образом rij=1, (ai,aj)Î R, 0 – в противном случае.-С использованием графа. Каждому бинарному отношению можно подставить в соответствие граф G(X,U), содержащий множество вершин Х, и множество ребер U. При этом вершины ajai соединяются дугой если упорядоченная пара ajai Î R. Так как отношения являются множеством упорядоченных пар, то для отношения можно определить те же операции, что и для множеств (объединение, пересечение, разность, дополнение, симметрическая разность).

Взвешенные графы

Ремарка



ans[start] = 0

q = очередь с приоритетом, хранящая пары (v, dst),

где dst - предполагаемое расстояние до v

добавить (start, 0) в q

пока q не пуста:

(v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё

извлечь (v, dst) из очереди

если ans[v] < dst: //мы уже обработали эту вершину, используя другой путь

перейти к следующей вершине

для каждой v -> u:

n_dst = dst + len(v -> u) //расстояние до u при прохождении через v

если n_dst < ans[u]: //если мы можем улучшить ответ

ans[u] = n_dst

добавить (u, n_dst) в q

Как видите, в очереди с приоритетом хранится не только номер вершины, но и вычисленное расстояние до неё, по которому и ведётся сортировка. Также возможна ситуация, при которой одна и та же вершина будет помещена в очередь несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам). В такой ситуации обрабатываем её только один раз (с минимальным возможным расстоянием).

57. Первый алгоритм Флойда-Уоршолла.

Алгоритм Флойда — Уоршелла — алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами с использованием метода динамического программирования. Это базовый алгоритм, так что тем кто его знает — можно дальше не читать.
Этот алгоритм был одновременно опубликован в статьях Роберта Флойда (Robert Floyd) и Стивена Уоршелла (Stephen Warshall) в 1962 г., хотя в 1959 г. Бернард Рой (Bernard Roy) опубликовал практически такой же алгоритм, но это осталось незамеченным.



Ремарка



Если граф не содержит рёбер с отрицательным весом, то для решения этой проблемы можно использовать алгоритм Дейкстры для нахождения кратчайшего пути от одной вершины до всех остальных, запустив его на каждой вершине. Время работы такого алгоритма зависит от типа данных, который мы будем использовать для алгоритма Дейкстры, это может быть как простая очередь с приоритетом, так и бинарная или фибоначчиева Куча, соответственно время работы будет варьироваться от O(V3) до O(V*E*log(V)), где V количество вершин, а E — рёбер. («О»-большое).

Если же есть рёбера с отрицательным весом, можно использовать алгоритм Беллмана — Форда. Но этот алгоритм, запущенный на всех вершинах графа, медленнее, время его работы O(V2*E), а в сильно «густых» графах аж O(V4).

58. Условия для графа быть деревом.

Граф называется деревом, если он связный и не имеет циклов.

Дерево — это связный ациклический граф.[1] Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.

59. Условия для графа быть корневым ориентированным деревом.

Корневое ориентированное дерево — это ориентированное дерево, в котором выделена одна вершина — корень (будем обозначать его ) так, что все вершины графа можно достичь из , двигаясь по ориентированным рёбрам.



60. Теоремы о m-арных ориентированных деревьях.


В теория графов, м-арное дерево (также известен как k-ари или же k-путь дерево) является укорененным дерево в котором каждый узел имеет не более м дети. А двоичное дерево это частный случай, когдам = 2, а тройное дерево другой случай с м = 3 это ограничивает количество его детей тремя.

  • А полныйм-арное дерево является м-арное дерево, где на каждом уровне каждый узел имеет либо 0, либо м дети.А полныйм-арное дерево является м-арное дерево, максимально занимающее пространство. Он должен быть полностью заполнен на всех уровнях, кроме последнего. Однако, если последний уровень не завершен, все узлы дерева должны быть «как можно дальше слева».[1]

  • А идеальном-арное дерево это полный[1]м-арное дерево, в котором все листовые узлы находятся на одной глубине.[2]

  М-арным назовем дерево у которого каждый из узлов кроме листьев содержит не более М деталей Если количество равно М то М-арное дерево будем называть полным.

Специальным случаем М-арног8о дерева является бинарное у которого М=2 несложно получить формулу для количество узлов полного М-арного дерева h:

Смотрите также файлы