Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 156
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ВОПРОСЫ и ответы К ЭКЗАМЕНУ
-
Комбинаторный признак умножения. Количество битовых строк длины k.
Пусть задана последовательность событий E1, E2, E3, …, Em таких, что событие Е1осуществляется n1способами, и если события E1, E2, E3,...,Ек-1осуществились, то событие Ек может осуществиться nкспособами. Тогда существует n1х n2х n3х … х nтспособов осуществления всей последовательности событий.
. Битовая строка – это строка, состоящая из элементов множества
{0, 1}, т.е. каждый из элементов имеет значение 0 или 1. Сколько существует битовых строк длины 5? Сколько существует битовых строк длины k?
Поскольку каждый символ строки может иметь значение 1 или 0, то
существует два варианта выбора для каждой позиции. Следовательно, существует 2 x 2 x 2 x 2 x 2 = 25 битовых строк длины 5. По аналогичным соображениям, имеется 2k битовых строк длины k.
-
Количество всех подмножеств k - элементного множества.
Число всех подмножеств из элементов равно N(M(A))=2^n
-
Комбинаторный признак сложения.
(Комбинаторный принцип сложения) Пусть S1, S 2, S3,... ,Sm – попарно непересекающиеся множества (т.е. SiSj = для всех i j), и пусть для каждого i, множество Si содержит niэлементов. Количество вариантов выбора из S1 или S2или S3 или ... или Smравно n1 + n2 + n3+ … + nm. На языке теории множеств утверждение теоремы имеет вид |S1 S2 S3 ... Sm|= |S1| + |S2| + |S3| + ... + |Sm|, где |S| обозначает количество элементов множества S.
-
Перестановки, размещения, сочетания без повторения.
Перестановками -называются наборы состоящие из одного и того элементов,следования элементов. Pn=n!
Размещение –называются упорядоченные наборы из элементов выбранных из n элементов, которые отличаются друг от друга, как порядком следования, так и составом элементов. m
A =n!/(n-m)!
n
Сочетание- называются
элементов выбранных из n элементов, которые отличаются друг
от друга составом элементов. m
С =n!/m!(n-m)!
n
-
Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов.
Формула бинома Ньютонадля натуральныхnимеет вид 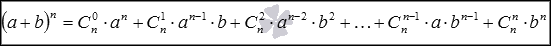 , где
, где 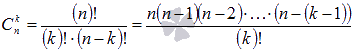 -биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).
-биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).
К примеру, известная формула сокращенного умножения "квадрат суммы" вида 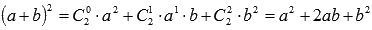 есть частный случай бинома Ньютона приn=2.
есть частный случай бинома Ньютона приn=2.
Выражение, которое находится в правой части формулы бинома Ньютона, называютразложениемвыражения(a+b)n, а выражение 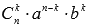 называют(k+1)-ым членом разложения,k=0,1,2,…,n.
называют(k+1)-ым членом разложения,k=0,1,2,…,n.
Биномиальные коэффициенты для различныхnудобно представлять в виде таблицы, которая называется арифметическийтреугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:
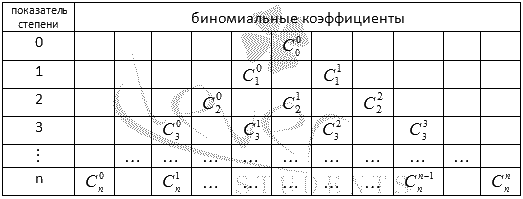
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральныхn:
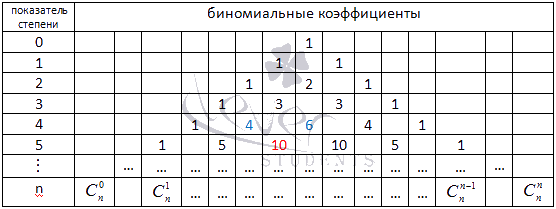
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Для коэффициентов бинома Ньютона справедливы следующие свойства:
-
коэффициенты, равноудаленные от начала и конца разложения, равны между собой 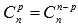 ,p=0,1,2,…,n;
,p=0,1,2,…,n;
-
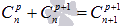 ;
;
-
сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона: 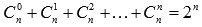 ;
;
-
сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Первые два свойства являются свойствами числа сочетаний.
-
Перестановки, размещения, сочетания с повторениями.
Перестановка – _
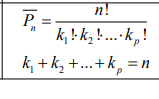
Размещение-
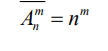
Сочетание-
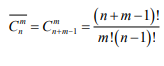
7. Признак клеток (Дирихле).
Принцип Дирихле — простой, интуитивно понятный и часто полезный метод для доказательства утверждений о конечном множестве. Этот принцип часто используется в дискретной математике, где устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках данное утверждение известно как «принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики.
Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, гдеn > mто, по крайней мере, в одной части будет более одного элемента.
На языке отображений эта формулировка означает, чтоесли в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.
Другая формулировка “ принципа Дирихле“:если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы двапредмета.
В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “. [2]
-
Признак математической индукции.
Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному. Определение 2

9. Высказывания. Отрицание, конъюнкция, дизъюнкция, их таблицы истинности.
Высказываниемназывается повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.
Отрицаниемвысказывания называется высказывание («не », «неверно, что »), которое истинно, когда ложно, и ложно, когда истинно.
Таблица истинности для отрицания:
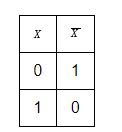
Конъюнкцией (логическим умножением) двух высказываний , называется высказывание (« и »), которое истинно только в том случае, когда и оба истинны.
Таблица истинности для конъюнкций:
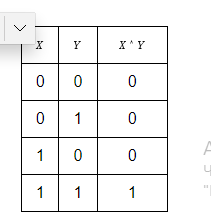
Дизъюнкцией (логическим сложением) двух высказываний , называется высказывание (« или »), которое истинно, когда хотя бы одно из них истинно.
Таблица истинности для дизъюнкций:
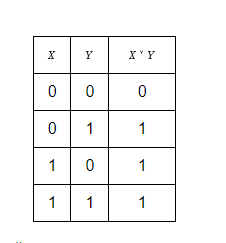
10. Импликация и эквиваленция, таблицы их истинности.
Импликацией двух высказываний , называется высказывание («если , то », « влечёт », «из следует », « имплицирует »), которое ложно тогда и только тогда, когда истинно, а ложно.
Таблица истинности для импликаций:
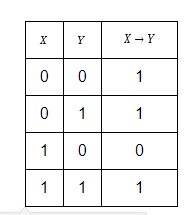
Эквивалентностью высказываний , называется высказывание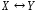 (« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда и оба истинны или ложны.
(« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда и оба истинны или ложны.
Таблица истинности для эквивалентности:
11. Эквивалентные высказывания. Теорема о свойствах логических эквивалентностей.
Эквиваленцией (или эквивалентностью) двух высказываний Х, У называется новое высказывание, которое считается истинным, когда оба высказывания Х, У, либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквиваленция высказываний Х, У обозначается символом  (или,
(или,
), читается «Х эквивалентно У» или « для того, чтобы Х, необходимо и достаточно, чтобы У», или «Х тогда и только тогда, когда У».
Комбинаторный признак умножения. Количество битовых строк длины k.
Количество всех подмножеств k - элементного множества.
Комбинаторный признак сложения.
Перестановки, размещения, сочетания без повторения.
Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов.
коэффициенты, равноудаленные от начала и конца разложения, равны между собой
сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона:
сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
Перестановки, размещения, сочетания с повторениями.
Признак математической индукции.
12. Тавтологии и противоречия, их свойства.
Формула называется тавтологией, если при любой интепретации она истинна; или противоречием, если при любой интепретации - ложна.
Теорема 3.1. Следующие формулы алгебры высказываний являются тавтологиями:
а) закон исключенного третьего;
б) закон отрицания противоречия;
в) закон двойного отрицания;
г) закон тождества;
д) закон контрапозиции;
е) закон силлогизма (правило цепного заключения);
ж) закон противоположности;
з) правило добавления антецедента ("истина из чего угодно");
и) правило "из ложного что угодно";
к) правило "модус поненс" (лат. modusponens);
л) правило "модус толленс" (лат. modustollens);
м) правило перестановки посылок;
н) правило объединения (и разъединения) посылок;
о) правило разбора случаев;
п) правило приведения к абсурду.
Доказательство. Отметим, что непосредственно из определений логических операций вытекает тождественная истинность формул а), б), в), г); для формулы д) доказательство имеется. Установим тождественную истинность формул л) и н) (для остальных проверьте самостоятельно).
Противоречие, как уже отмечалось, является одним из четырёх основных законов логики.
Причём, из определения закона видно, что в данном формально логическом законе имеется в виду не всякое противоречие. а только один из видов противоречия. а именно, противоречие формально-логическое. У логического противоречия нет точного прототипа в природе и обществе. Поэтому возникающее противоречие в процессе исследования на тавтологию
рассматриваемых в сравнении формул.
13. Умозаключения и правила вывода, доказательство от противного.
Умозаключения, как и понятия и суждения, являются формой абстрактного мышления. С помощью многообразных видов умозаключений опосредованно (т. е. не обращаясь к органам чувств) мы можем получать новые знания. Умозаключать можно при наличии одного или нескольких суждений (называемых посылками), поставленных во взаимную связь. Возьмем пример умозаключения:
Все углероды горючи.
Алмаз - углерод.
Алмаз горюч.
Умозаключение - форма мышления, в которой из одного или нескольких суждений на основании определенных правил вывода получается новое суждение, с необходимостью или определенной степенью вероятности следующее из них.
Умозаключения делятся на такие виды: дедуктивные, индуктивные, по аналогии. Умозаключения могут быть логически необходимыми, т. е. давать истинное заключение, и вероятностными (правдоподобными), т. е. давать не истинное заключение, а лишь с определенной степенью вероятности следующее из данных посылок (при этом в качестве посылок могут быть и ложные суждения).
Схема умозаключения «от противного» такова:«Если из А следует В, то из не В следует не А».Другими словами, если верно АВ, то верно
Покажем справедливость
14. Полнота в логике высказываний. Штрих Шеффера и стрелка Пирса.
В исчислении высказываний, кроме явных определений, существуют неявные. К ним относится
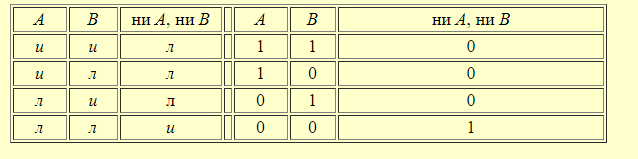
стрелка Пирса,АВ .Это сложное высказывание, которое означает "НиА, ниВ".Например, "
новое здание было ни высоким (А), ни низким(В)". Это высказывание истинно только тогда, когда ложны
оба высказывания, входящие в это сложное высказывание.
Таблица истинности сложного высказывания видаАВ
выглядит следующим образом:
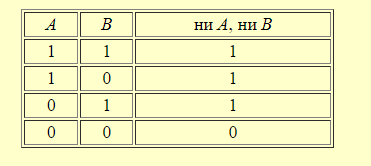
Для сравнения приведём таблицу истинности для дизъюнкции А В, в котором союз "или" употреблён в соединительно -разделительном смысле.
Одно из направлений современной неклассической математической логики, в котором не применяется операция отрицания называется "положительная логика". Одной из таких логических построений является логика, построенная с помощью одного функтора логического знака операции) "/" , который называется "штрих Шеффера".
Например,А/Возначает: "АиВнесовместны" или "Неверно, чтоА и В". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны.
Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либоАложно, либоВложно , либоА и Вложны одновременно. Оно ложно и в ом случае, если истинны иАи Водновременно. Действительно, если вместо А подставить высказывание
"2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", тоА/Вдадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом
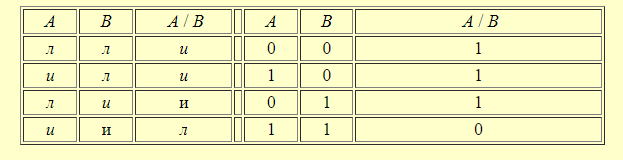
Как видно из таблицы, операция со знаком "/" является противоположной операции операции со знаком "". Операция истинностного значения сложного высказывания А В выглядит так:
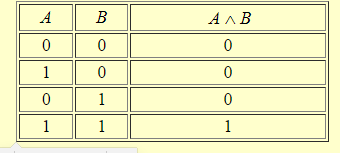
На этом основании всегда можно вывести формулу:А/В≡
Сложное высказывание можно выразить и через дизъюнкцию, которая примет следующий вид: А/В ≡
С помощью штриха Шиффера можно выразить все другие связки исчисления высказываний, что и сделал сам Шиффер. построив всю теорию исчислений высказываний с помощью только одного знака операции. В этой системе действительны следующие равнозначности:
Ā ≡ А / А"ОтрицаниеАравносильно тому, чтоА и Анесовместны"
АВ≡
АВ ≡
АВ ≡
Операция штрих Шеффера коммутативна:
А / В≡ В /А
Но операция не подчиняется закону ассоциативности:
А / (В / С) ≠ (А / В) / С
Полнота логических исчислений — выводимость в исчислении (логической системе) всех утверждений (предложений, формуЛит.п.), обладающих некоторым подразумеваемым для этого исчисления свойством. Напр., П. классического исчисления