Файл: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 163

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВОПРОСЫ и ответы К ЭКЗАМЕНУ Комбинаторный признак умножения. Количество битовых строк длины k. Пусть задана последовательность событий E1, E2, E3, …, Em таких, что событие Е1осуществляется n1способами, и если события E1, E2, E3,...,Ек-1осуществились, то событие Ек может осуществиться nкспособами. Тогда существует n1х n2х n3х … х nтспособов осуществления всей последовательности событий.. Битовая строка – это строка, состоящая из элементов множества{0, 1}, т.е. каждый из элементов имеет значение 0 или 1. Сколько существует битовых строк длины 5? Сколько существует битовых строк длины k?Поскольку каждый символ строки может иметь значение 1 или 0, тосуществует два варианта выбора для каждой позиции. Следовательно, существует 2 x 2 x 2 x 2 x 2 = 25 битовых строк длины 5. По аналогичным соображениям, имеется 2k битовых строк длины k. Количество всех подмножеств k - элементного множества. Число всех подмножеств из элементов равно N(M(A))=2^n Комбинаторный признак сложения.  (Комбинаторный принцип сложения) Пусть S1, S 2, S3,... ,Sm – попарно непересекающиеся множества (т.е. SiSj = для всех i  j), и пусть для каждого i, множество Si содержит niэлементов. Количество вариантов вы­бора из S1 или S2или S3 или ... или Smравно n1 + n2 + n3+ … + nm. На языке теории множеств утверждение теоремы имеет вид |S1 S2 S3 ... Sm|= |S1| + |S2| + |S3| + ... + |Sm|, где |S| обозначает количество элементов множества S. Перестановки, размещения, сочетания без повторения. Перестановками -называются наборы состоящие из одного и того элементов,следования элементов. Pn=n!Размещение –называются упорядоченные наборы из элементов выбранных из n элементов, которые отличаются друг от друга, как порядком следования, так и составом элементов. mA =n!/(n-m)!nСочетание- называютсяэлементов выбранных из n элементов, которые отличаются другот друга составом элементов. mС =n!/m!(n-m)!n Бином Ньютона. Треугольник Паскаля. Свойства биномиальных коэффициентов. Формула бинома Ньютонадля натуральныхnимеет вид  , где   -биномиальные коэффициенты, представляющие из себя сочетания изnпоk,k=0,1,2,…,n, а "!" – это знак факториала).К примеру, известная формула сокращенного умножения "квадрат суммы" вида   есть частный случай бинома Ньютона приn=2.Выражение, которое находится в правой части формулы бинома Ньютона, называютразложениемвыражения(a+b)n, а выражение   называют(k+1)-ым членом разложения,k=0,1,2,…,n.Биномиальные коэффициенты для различныхnудобно представлять в виде таблицы, которая называется арифметическийтреугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид: Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральныхn: Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.Для коэффициентов бинома Ньютона справедливы следующие свойства: коэффициенты, равноудаленные от начала и конца разложения, равны между собой  ,p=0,1,2,…,n; ; сумма биномиальных коэффициентов равна числу2, возведенному в степень, равную показателю степени бинома Ньютона:  ; сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах. Первые два свойства являются свойствами числа сочетаний. Перестановки, размещения, сочетания с повторениями. Перестановка – _ Размещение- Сочетание- 7. Признак клеток (Дирихле). Принцип Дирихле — простой, интуитивно понятный и часто полезный метод для доказательства утверждений о конечном множестве. Этот принцип часто используется в дискретной математике, где устанавливает связь между объектами («кроликами») и контейнерами («клетками») при выполнении определённых условий. В английском и некоторых других языках данное утверждение известно как «принцип голубей и ящиков, когда объектами являются голуби, а контейнерами — ящики.Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, гдеn > mто, по крайней мере, в одной части будет более одного элемента.На языке отображений эта формулировка означает, чтоесли в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.Другая формулировка “ принципа Дирихле“:если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы двапредмета.В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “. [2] Признак математической индукции. Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному. Определение 2 9. Высказывания. Отрицание, конъюнкция, дизъюнкция, их таблицы истинности.Высказываниемназывается повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.Отрицаниемвысказывания  называется высказывание («не », «неверно, что »), которое истинно, когда ложно, и ложно, когда истинно.Таблица истинности для отрицания: Конъюнкцией (логическим умножением) двух высказываний  , называется высказывание (« и »), которое истинно только в том случае, когда и оба истинны.Таблица истинности для конъюнкций: Дизъюнкцией (логическим сложением) двух высказываний  , называется высказывание (« или »), которое истинно, когда хотя бы одно из них истинно.Таблица истинности для дизъюнкций: 10. Импликация и эквиваленция, таблицы их истинности.Импликацией двух высказываний  ,  называется высказывание  («если , то », « влечёт », «из следует », « имплицирует »), которое ложно тогда и только тогда, когда истинно, а ложно.Таблица истинности для импликаций:  Эквивалентностью высказываний  , называется высказывание (« эквивалентно », « тогда и только тогда, когда », «для того, чтобы , необходимо и достаточно, чтобы »), которое истинно тогда и только тогда, когда  и  оба истинны или ложны.Таблица истинности для эквивалентности: 11. Эквивалентные высказывания. Теорема о свойствах логических эквивалентностей.Эквиваленцией (или эквивалентностью) двух высказываний Х, У называется новое высказывание, которое считается истинным, когда оба высказывания Х, У, либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.Эквиваленция высказываний Х, У обозначается символом  (или,

22. Булева алгебра.Булевой алгеброй называется дистрибутивная структура с неравными друг другу единицей 1 и нулем 0, в которой всякий элемент имеет дополнение. Булева алгебра всегда содержит не менее двух элементов. Алгебра, содержащая только 1 и 0, называется вырожденной.23. Основные законы и свойства операций Булевой алгебры.Как любая алгебраическая система булева алгебра базируется на совокупности некоторых предположений, которые принято называть аксиомами, т.е предположениями не требующими доказательств. Аксиомы определяются для двух логических значений 1 ( "ИСТИНА" ) и 0 ( "ЛОЖЬ" ) и операций логического умножения (конъюнкции), которая обозначается " & ", " · " или не обозначается вовсе, логического сложения (дизъюнкции), которая обозначатся " v ", "+", и отрицания ( инверсии ), которая обозначается горизонтальной чертой (" - ") над переменной или выражением, например, . Булевой переменной, обозначаемой обычно xi , называется переменная принимающая два логических значения { 0, 1 }.Ниже приведены аксиомы булевой алгебры относительно дизъюнкции, конъюнкции и отрицания.Аксиомы конъюнкции 0·* 0 = 0 ; 1·* 1 = 1 ; 0·* 1 = 1·* 0 = 0 ;Аксиомы дизъюнкции 0 v 0 = 0 ; 1 v 1 = 1 ; 0 v 1 = 1 v 0 = 1 ;Аксиомы отрицания Если x = 0 , то ˆх = 1 ;Если x = 1 , то ˆх = 0 ;Следующие 5 правил обычно называют теоремами булевой алгебры. Особенностью теорем булевой алгебры является то, что для их доказательства пользуются простой подстановкой значений булевых переменных. Это обусловлено тем, что переменные могут принимать только 2 значения - 0 и 1.Операции с константами : Идемпотентность (тавтология, повторение) :  Для n переменных:  Противоречие :Правило "исключенного третьего" :Двойное отрицание (инволюция) :Следующие 4 правила обычно называют законами или тождествами булевой алгебры.Ассоциативность ( ассоциативный закон ) :   Коммутативность ( коммутативный закон ) :   11. Дистрибутивность ( дистрибутивный закон ) :конъюнкции относительно дизъюнкции: дизъюнкции относительно конъюнкции: 24. Отношения множеств. Область определения и множество значений отношения. Обратное отношение. Область определения отношения R – это подмножество всех элементов х множества Х, для которыхнайдется элемент y, связанный с данным элементом отношением R. Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R (). Пример: Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X. Итак, если R — отношение на множестве X, то R X X. Множество всех первых элементов пар из R называется областью определения отношения R. Множеством значений отношения R называется множество всех вторых элементов пар из R. Обратное отношение (отношение, обратное к R) — это двухместное отношение, состоящее из пар элементов (у, х), полученных перестановкой пар элементов (х, у) данного отношения R. Обозначается: R−1. Для данного отношения и обратного ему верно равенство: (R−1)−1= R. Взаимо-обратные отношения(взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого. 25. Специальные свойства отношений на А. Частично упорядоченные множества.Бинарным отношением на множестве А называется подмножество его квадрата RÍ A2. Бинарным отношением между множествами А и В называются подмножество принадлежащее декартовому произведению 2-х множеств: RÍ АхВ.Если упорядоченная пара (а1, а2) принадлежит отношению R, то говорят что а1 R а2, то есть между элементом а1 и а2 уст-но отношение R.Областью определения бинарного отношения называется множество элементов а, в котором в принадлежит бинарному отношению: þR={a|bÎ aRb}.Областью значения бинарного отношения называют множество b, в котором а принадлежит бинарному значению:PR={b|aÎ aRb }.Обратное отношение для отношения R называется отношение: R-1={(b,a)|(a,b) Î R }.Отношение можно задать:-с помощью любого способа задания множеств-С помощью матрицы бинарного отношения. Матрица бинарного отношения это квадратная матрица R элементы которой определяются следующим образом rij=1, (ai,aj)Î R, 0 – в противном случае.-С использованием графа. Каждому бинарному отношению можно подставить в соответствие граф G(X,U), содержащий множество вершин Х, и множество ребер U. При этом вершины ajai соединяются дугой если упорядоченная пара ajai Î R. Так как отношения являются множеством упорядоченных пар, то для отношения можно определить те же операции, что и для множеств (объединение, пересечение, разность, дополнение, симметрическая разность).

Взвешенные графы

Ремарка


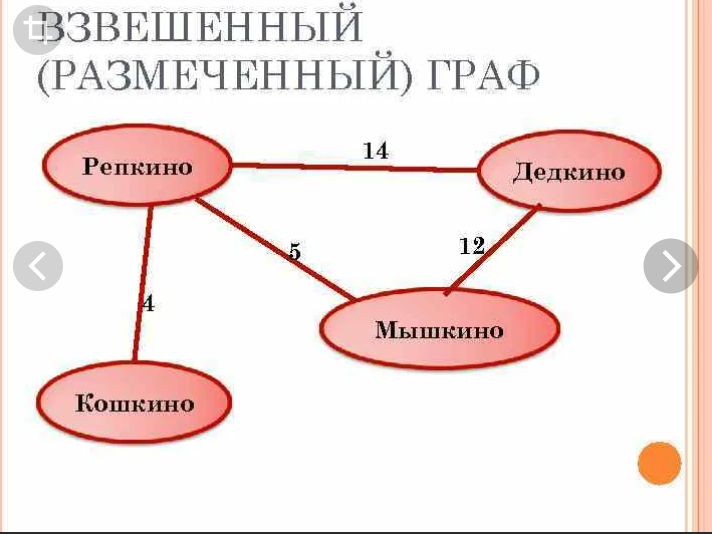
Размеченныйграф- этоориентированныйилинеориентированный граф G= (V, E), снабженный одной или двумя функциями разметки вида: l: V -> M и c: E -> L, где M и L - множества меток вершин и ребер, соответственно.



40. Деревья, ориентированные деревья.

Ориентированным деревом называют бесконтурный ориентированный граф, у которого полустепень захода любой вершины не больше 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, полустепень захода которой равна 0.





Опираясь на данное определение, можно доказать, что в ориентированном дереве любая вершина достижима из корня.





Отметим, что из определения 5.6 нельзя убрать требование бесконтурности ориентированного графа, поскольку бесконтурность не вытекает из других условий. Например, на рис. 5.13 изображен ориентированный граф, не являющийся ориентированным деревом, хотя полустепени захода всех вершин не больше 1 и ровно одна вершина имеет полустепень захода, равную 0.





Определение 5.7.Вершину v ориентированного дерева называют потомком (подлинным потомком) вершины, если существует путь изв(путь ненулевой длины изв). В этом же случае вершинуназывают предком (подлинным предком) вершины, а если длина пути извравна 1, то вершинуназывают сыном вершины, которая при этом вполне естественно именуется отцом вершины. Вершину, не имеющую потомков, называют листом.
41. Корневые деревья. Остовное дерево графа.

Дерево – это граф без циклов.

Дерево называетсякорневым, если оно ориентированно, и из какой-то вершины (называемойкорнем) можно попасть во все остальные.

Примеры корневых деревьев:

  • наследование классов в языках программирования (если множественное наследование запрещено),

  • дерево факторизации числа на простые (в общем случае не уникальное),

  • иерархия в какой-нибудь организации,

  • дерево парсинга математичеких выражений.

Задачи на корневые деревья весьма бесполезны в реальной жизни, но зато очень интересны с алгоритмической точки зрения, и поэтому часто встречаются на олимпиадах по программированию.

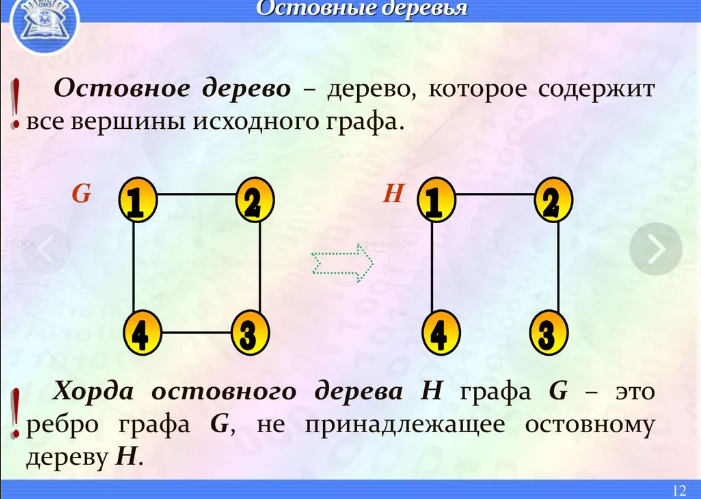
О́стовное де́рево графа (англ. Spanning tree) — это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все � вершин исходного графа и содержит �−1ребро.


42. Две задачи о Кенигсбергских мостах. Пути и цели Эйлера.

Задача состояла в следующем: найти маршрут прохожде­ния всех четырех частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту. Легко, конечно, попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей.



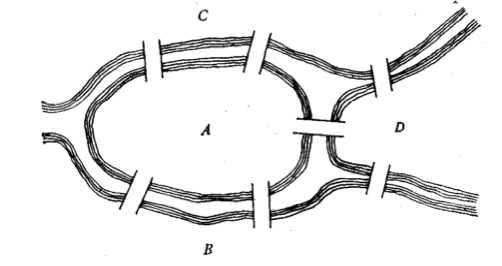
Исключительный вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность та­кого маршрута.

Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился граф. Утверждение о несуществовании положительного решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом данный граф.

ПустьG(V,E) – граф. Цикл, который включает все ребра и вершины графаG, называетсяэйлеровым циклом. Граф, в котором существует эйлеров цикл называетсяэйлеровым.

Связный граф является эйлеровым тогда и только тогда, когда степень каждой его вершины четная.

Определение 10.2.ПустьG(V,E) – граф. Путь, который включает каждое ребро графаGтолько один раз называетсяэйлеровым путем. Эйлеров путь, который не является циклом называетсясобственным эйлеровым путем.

Сформулируем теорему (без доказательства), в которой описано условие, при котором граф имеет собственный эйлеров путь.


Теорема 10.2.Граф (мультиграф или псевдограф) имеет собственный эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины имеют нечетную степень.

По этой теореме получается, что задача о кенигсбергских мостах так же не имеет и эйлерова пути.

Аналогично можно ввести понятие эйлерова цикла для ориентированного графа и условие существования эйлерова цикла в орграфе.

Определение 10.3.ПустьG(V,E) - ориентированный граф. Ориентированный цикл, который включает все ребра и вершины графаG, называетсяэйлеровым циклом.

Теорема 10.3.Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и полустепень захода каждой вершины равна ее полустепени исхода.
43. Матрица инцидентности и матрица смежности. Теоремы о к-путях.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро (дуга) и вершина). В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.
Матрица смежности - это вид представления графа в виде матрицы, когда пересечение столбцов и строк задаёт дуги. Используя матрицу смежности, можно задать вес дуг и ориентацию. Каждая строка и столбец матрицы соответствуют вершинам, номер строки соответствует вершине, из которой выходит дуга, а номер столбца - в какую входит дуга.
Если между двумя вершинами графа существует путь, то между ними существует вершинно-простой путь.

44. Алгоритм Уоршолла.

Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.


45. Гиперкубы. Построение кода Грея для к+1.

Правила построения кода Грея дляк +1 состоят в следующем.

  • 1. Поместить 1 перед каждой вершиной в ^-списке ^-мерного куба. Вершины, смежные в /с-мерном кубе, с приставленной впереди 1 остаются смежными в(к +1)-мерном кубе.

  • 2. Поместить 0 перед каждой вершиной в реверсированном ^-списке ^-мерного куба. Вершины, смежные в ^-мерном кубе, с приставленным впереди 0 остаются смежными в(к+ 1)-мерном кубе.

  • 3. Разместить последовательность, сформированную в пункте 2, после последовательности, сформированной в пункте 1.

  • 4. Каждая последовательная пара вершин в(к+ 1)-мерном списке(к+ 1)-мерного куба является смежной. Первая вершина(к +1)-списка также является смежной с последней вершиной списка.

Подсеткойпонимают граф, вершины которого заданы массивом размератхпи для которого две вершины, соседствующие в одной и той же строке или столбце массива, являются смежными как вершины графа. Возможно ли длят<2кип<21построитьподграф(к+/)-мерного куба,

Гиперку́б— обобщениекубана случай с произвольным числом измерений.Гиперкубом размерностиΝназывается множество точек вΝ-мерном евклидовом пространстве, удовлетворяющее неравенствам∀�:−�2<��<�2, где�— длина ребра гиперкуба.

Также можно определить гиперкуб какдекартово произведениеΝравных отрезков.


46. Построение (m×n) – сетки с помощью кода Грея.

Для построениякода Грея выполним следующие шаги:

  1. исходя из мощности алфавита, определим размер nxm таблицы для построения кода Грея, где n – число строк, m – число столбцов таблицы. Для этого будем последовательно наращивать число столбцов и число строк, начиная с одной строки и одного столбца, каждый раз проверяя, не достигнут ли требуемый размер таблицы. При этом схема наращивания числа строк и столбцов будет определяться следующим образом: число столбцов на каждом шаге итерации равно или на 1 превышает число строк



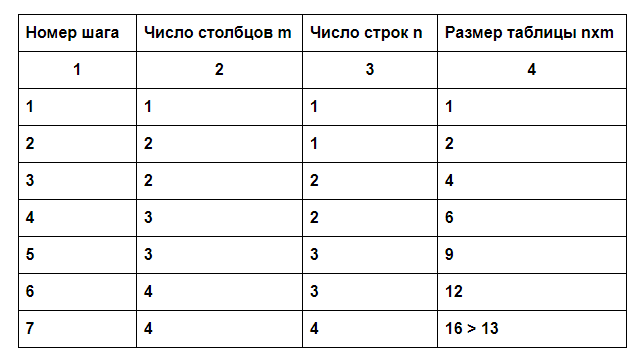
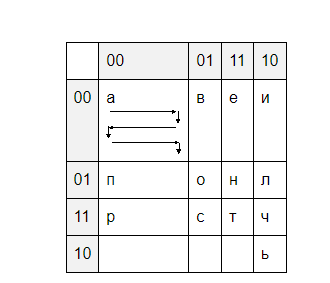
Поскольку на седьмом шаге итерации удалось достичь требуемого размера таблицы, определение ее размеров закончено. Таким образом, получена таблица размером 4х4,

  1. строки и столбцы таблицы пронумеруем двоичными числами из множества {00, 01, 10, 11}, элементы которого сами являются кодами Грея (затушеванные ячейки таблицы 4.2),



  1. разместим в ячейках таблицы упорядоченные по алфавиту символы исходного множества (см. графу 1 таблицы 4.3) в направлении, указанном стрелками в таблице 4.2,

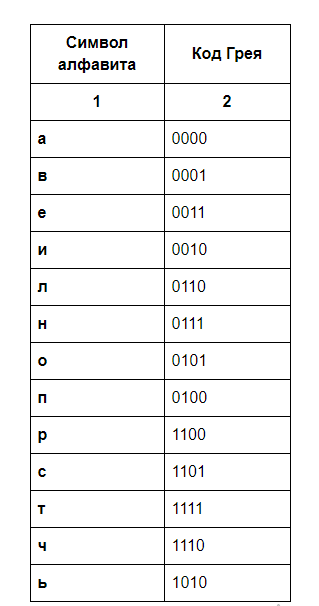
  2. для формирования кода Грея по каждому символу объединим номера строки и столбца ячейки, в которой находится символ. Получим графу 2 таблицы 4.3.


47. Гомоморфизм, изоморфизм и гомеоморфизм графа.

Определение 5.14.Отображениемножества вершин графав множество вершин графаназывают гомоморфизмом графов (графав граф), если для любых двух вершин, смежных в первом графе, их образы при отображениисмежны во втором графе, т.е. если


Биективный гомоморфизм, такой, что любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т.е.



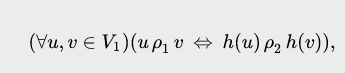
называют изоморфизмом графови(графана граф), а графыи— изоморфными, что записывают в виде

Два графа G  и G’ гомеоморфны, если существует изоморфизм некоторого подразделения графа G и некоторого подразделения графа G’. Если рёбра графа понимать как отрезки, соединяющие вершины (как обычно рисуется на иллюстрациях), то два графа гомеоморфны в контексте теории графов, когда они гомеоморфны в топологическом смысле.

Смотрите также файлы